Навигация
Визначення і установка кольору для малювання
3. визначення і установка кольору для малювання
4. малювання рекурсивної частини кривої з допомогою процедур A(i), B(i), C(i) D(i).
Потім виконується збільшення лічильника циклу на 1 і перевірка умови закінчення циклу. При досягненні лічильником циклу значення змінної Count здійснюється вихід з циклу й побудова кривої Серпінського і-го порядку завершується. На цьому програма завершує свою роботу.
При роботі з програмою встановлюються такі вимоги до системи:
ü x86 персональний комп'ютер (386 мінімум; 486, Pentium, чи Pentium Pro рекомендується)
ü Microsoft DOS 3.30 чи вище
ü Microsoft Windows 3.1, Microsoft Windows for Workgroups, Microsoft Windows 95, Microsoft Windows NT 3.51 чи 4.0
ü 512 Kb RAM
ü 5 Kb вільного простору на жорсткому диску
ü Встановлений інтерпретатор XLisp версії 2.1 чи вище
Для запуску програми необхідно:
q Увімкнути комп'ютер
q Завантажити інтерпретатор XLisp c параметром «Sierpins.lsp»: C:\XLISP\XLISP.EXE SIERPINS.LSP[1] Ã
q У відповідь на запрошення XLisp увести: (SierpinskiCurve 4)Ã
Висновки
Завершивши роботу над курсовим проектом можна зробити висновок про те, що мені вдалося досягти своєї мети і розробити програму побудови кривих Серпінського. За допомогою засобів алгоритмічної мови Lisp було створено програму Serp‚ яка дозволяє будувати криві Серпінського за допомогою рекурсивних процедур. Використання чотирьох рекурсивних процедур дало змогу досить просто справитись з поставленою задачею..
Розробка даної програми дала мені змогу оволодіти основними засобами програмування на алгоритмічній мові Lisp та здобути практичні навички розробки програм з використанням інтерпретатора PC-Lisp версії 3.0.
Завдяки використанню мови програмування Lisp розроблена програма вийшла лаконічною і водночас легкою для читання й розуміння, а розроблені рекурсивні графічні процедури можуть бути використані при розв'язуванні інших, можливо набагато складніших програм.
Список використаної літератури
1. “Алгоритм + структура даних = програма”, H.Вірт.
2. “XLisp-Plus 2.1 Programmers Manual”, David Michael Betz
Додаток А. Блок-схема алгоритму
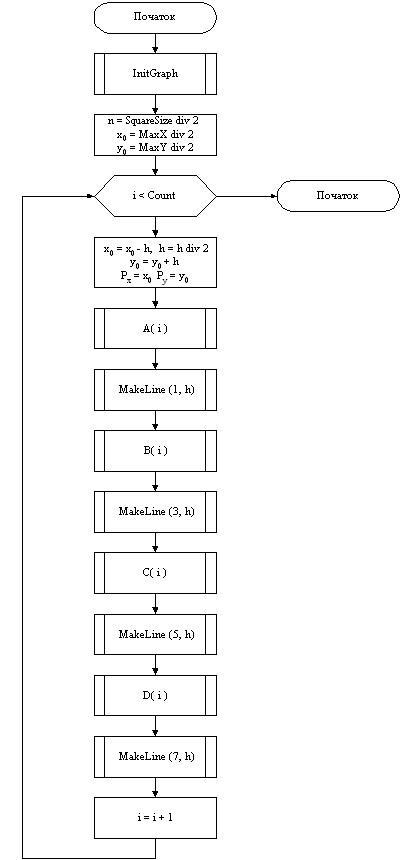
Схема алгоритму процедури A
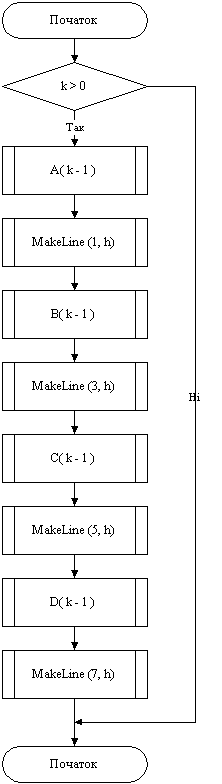
Додаток Б. Текст програми
;; SIERPINS.LSP для XLISP версії 2.1
;; ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
;; Програма побудови кривих Серпінського i-го порядку.
;;
;; ЗАПУСК: > (SierpinskiCurve 4)
;;
;;
( defvar *VMode* 18 ) ;Відео режим за замовчуванням
( defvar *Max* 640 ) ;Максимальна ширина екрана за замовчуванням
( defvar *Max* 480 ) ;Максимальна висота екрана за замовчуванням
( defvar *SquareSize* 256 ) ;Розмір області для побудови
;;
;; Функція ініціалізує графічний режим, установлює перемінні
;; *Max* *Max* *SquareSize* відповідно до обраного режиму
;;
(
defun InitGraph()
(
case *VMode*
( 4 ;320x200 Color
( mode 4 )
( setq *MaxX* 320 *MaxY* 200 *SquareSize* 128 ) )
( 16 ;640x350 Color
( mode 16 )
( setq *MaxX* 640 *MaxY* 350 *SquareSize* 128 ) )
( 18 ;640x480 Color
( mode 18 ) )
( 106 ;800x600 Color
( mode 106 106 800 600 )
( setq *MaxX* 800 *MaxY* 600 *SquareSize* 512 ) )
( t ( error Unsupported graphics mode: *VMode* ) )
)
)
;;
;; Функція реалізує затримку на заданий час
;;
(
defun pause ( time )
( let ( ( fintime ( + ( * time internal-time-units-per-second )
( get-internal-run-time ) ) ) )
( loop ( when ( > ( get-internal-run-time) fintime )
( return-from pause ) ) ) )
)
;;
;; Функція цілочисленого розподілу
;;
(
defun div ( a b ) ( round ( / a b ) )
)
;;
;; Функція малювання прямої:
;; Параметри: <Direction> - напрямок малювання (0-7)
;; <Size> - довжина прямої
;;
(
defun Line( Direction Size )
( setq x Px y Py )
(
case Direction
( 0 ( setq x ( + x Size) ) )
( 1 ( setq x ( + x Size ) y ( - y Size ) ) )
( 2 ( setq y ( - y Size) ) )
( 3 ( setq x ( - x Size ) y ( - y Size ) ) )
( 4 ( setq x ( - x Size) ) )
( 5 ( setq x ( - x Size ) y ( + y Size ) ) )
( 6 ( setq y ( + y Size) ) )
( 7 ( setq x ( + x Size ) y ( + y Size ) ) )
)
( move Px Py x y )
( setq Px x Py y )
)
;;
;; Функції A, B, C, D - рекурсивні функції малювання
;;
(
defun A ( k )
( cond ( ( > k 0 )
( A ( - k 1 ) ) ( Line 1 h )
( B ( - k 1 ) ) ( Line 0 ( * 2 h ) )
( D ( - k 1 ) ) ( Line 7 h )
( A ( - k 1 ) )
) )
)
(
defun B ( k )
( cond ( ( > k 0 )
( B ( - k 1 ) ) ( Line 3 h )
( C ( - k 1 ) ) ( Line 2 ( * 2 h ) )
( A ( - k 1 ) ) ( Line 1 h )
( B ( - k 1 ) )
) )
)
(
defun C ( k )
( cond ( ( > k 0 )
( C ( - k 1 ) ) ( Line 5 h )
( D ( - k 1 ) ) ( Line 4 ( * 2 h ) )
( B ( - k 1 ) ) ( Line 3 h )
( C ( - k 1 ) )
) )
)
(
defun D ( k )
( cond ( ( > k 0 )
( D ( - k 1 ) ) ( Line 7 h )
( A ( - k 1 ) ) ( Line 6 ( * 2 h ) )
( C ( - k 1 ) ) ( Line 5 h )
( D ( - k 1 ) )
) )
)
;;
;; Головна процедура
;; Параметри: <Count> - кількість ітерацій
;;
(
defun SierpinskiCurve ( Count )
( InitGraph ) ;Установка графічного режиму
( setq h ( div *SquareSize* 4 ) ) ;Обчислення довжини лінії
( setq x0 ( div *Max* 2 ) ) ;Обчислення початкової точки
( setq y0 ( + ( div *Max* 2 ) h ) ) ;для малювання
( ;Основний цикл
do (( i 1 )) ;Ініціалізація лічильника
(( eql i ( + Count 1 ) ) 'Done ) ;Умова завершення
( setq x0 ( - x0 h ) ) ;Обчислення координат початкової
( setq h ( div h 2 ) ) ;крапки для малювання і
( setq y0 ( + y0 h ) ) ;одиничної довжини лінії
( setq Px x0 Py y0 ) ;Установка пера
( color i ) ;Установка кольору для малювання
( A i ) ( Line 1 h ) ;Малювання
( B i ) ( Line 3 h )
( C i ) ( Line 5 h )
( D i ) ( Line 7 h )
( pause 1.0 ) ;Затримка
( setq i ( + i 1 )) ;Інкремент лічильника
) ;Кінець основного циклу
)
( print Try (SierpinskiCurve 4) ) ;Підказка
Додаток В. Тест програми
Тест проводився на робочій станції з наступною конфігурацією:
q Pentium 166
q 32 Mb RAM
q SyncMaster 17Glsi
q S3 Trio64V+
q Windows 95
Інтерпретатор XLisp був запущений у вікні MS-DOS.
Програма тестувалась при значеннях параметра Count від 1 до 4. У результаті тестів були отримані наступні зображення на екрані монітора :

Малюнок 3
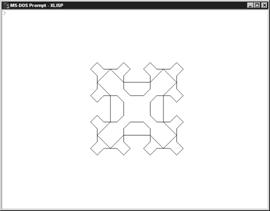
Малюнок 4
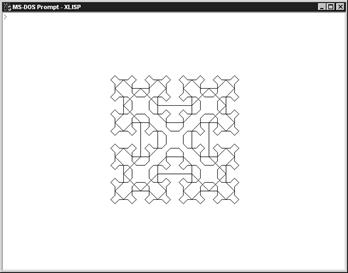
Малюнок 5

Малюнок 6
[1] Даний приклад передбачає, що XLisp встановлено в каталозі C:\XLISP и його запуск проводиться в режимі MS-DOS.
0 комментариев