Навигация
ОПИС АЛГОРИТМІВ РОЗВ’ЯЗАННЯ ЗАДАЧІ
3. ОПИС АЛГОРИТМІВ РОЗВ’ЯЗАННЯ ЗАДАЧІ
Опишемо алгоритм роботи усіх функцій усіх модулів нашого проекту. Почнемо з основного main.cpp. Містить дві функції void avtor() та void main(). Перша з них виводить інформацію про автора проекту. Алгоритм роботи дуже простий: очистка екрану -> задання кольору -> отримання розмірів екрану -> замальовування екрану вибраним кольором -> задання кольору та стилю тексту -> вивід тексту на екран.
Друга функція – головна. Вона є фактично монітором нашого проекту, спочатку ініціалізує графічний режим, підключаючи BGI драйвер EGAVGA.BGI, потім запускає електронну титульну сторінку курсової роботи, потім будує графік функції, корені якої нам потрібно знайти, використовуючи метод дихотомії знаходить корінь на вказаному з клавіатури проміжку з вказаною точністю, демонструє метод дихотомії графічно та зрештою виводить головне меню на екран. Після цього програма очікує вибору користувача.
Тепер перейдемо до додаткових модулів.
Модуль tytulka.cpp містить лише одну функцію void tytulka(), що виводить на екран електронну титульну сторінку розробника курсової роботи. Алгоритм роботи дуже простий і подібний до алгоритму функції void avtor().
Модуль grafik.cpp містить функцію void grafik(), що будує Декартову систему координат та графік функції на ній. Алгоритм роботи теж подібний до алгоритму функції void avtor(), але є додатково цикл обчислення значення функції для точок з проміжку [-2;2] з кроком 0,01 та побудова кривої, що з’єднує ці точки.
Модуль dyhotom.cpp містить дві функції: double f(double x) – обчислення значення вказаної в завданні функції для певного значення х, void dyhotom() – реалізація чисельного методу знаходження кореня рівняння на вказаному проміжку з вказаною точністю. Проміжні результати виконання записуються у файли KORENI.TXT та MEGI.TXT.
Алгоритм наступний:
ввід інтервалу (a;b) та потрібної точності (D)
поки |a-b| < D виконувати
початок циклу
![]()
якщо f(a)×f(с) > 0
то a:=c
інакше b:=c
кінець циклу
вивід значення кореня ![]()
Модуль demon.cpp містить одну функцію void demon(), що графічно демонструє роботу функції void dyhotom(), використовуючи проміжні результати виконання, що записані у файли KORENI.TXT та MEGI.TXT. Алгоритм роботи дуже простий і подібний до алгоритму функцій void avtor() та void tytulka().
Алгоритми всіх функцій у вигляді блок-схем подані в додатку.
4. РОЗРОБКА ТА ВИКОНАННЯ ТЕСТОВОГО ПРИКЛАДУ
Перед нами стоїть задача перевірити вірність виконання поставленого перед нами завдання.
Побудуємо графік функцій ![]() та
та ![]() використовуючи математичний пакет MathСad (рисунок 4.1):
використовуючи математичний пакет MathСad (рисунок 4.1):
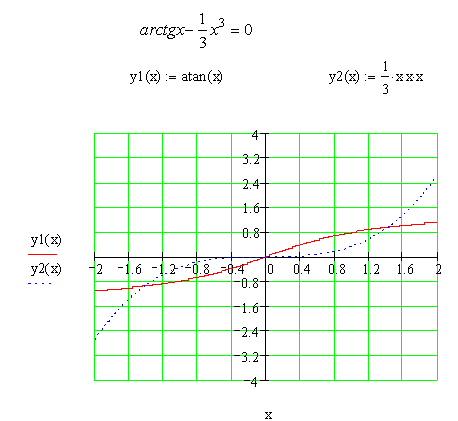
Рисунок 4.1 – Зображеня вказаних функцій в середовищі MathCad
Запускаємо на виконання виконавчий файл нашого проекту. Спочатку бачимо зображення електронної титульної сторінки (рисунок 4.2).
Рисунок 4.2 - Зображення електронної титульної сторінки
Програма чекає, поки буде натиснута довільна кнопка. Що ми і робимо. З’являється графік функцій (рисунок 4.3). Порівняємо два рисунки: 4.1 та 4.3. Бачимо повне співпадіння.
Нам потрібні проміжки, де дві функції перетинаються. Таких проміжків є три: окіл нуля, проміжок від -2 до -1, проміжок від 1 до 2.
Знову натискаємо довільну кнопку. З’являється вікно із запитом на введення даних (рисунок 4.4). Вводимо послідовно значення межі проміжка та похибки. Отримаємо:
a=1
b=3
eps=0.2
-------------------------------------------------
korin rivnjannja 1.0625
kilkist iteratsij 4
пробуємо всі проміжки:
a=1
b=2
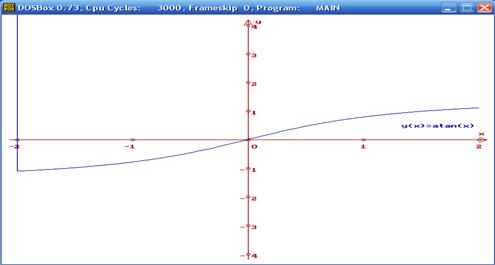
Рисунок 4.3 - Зображення графіка функції
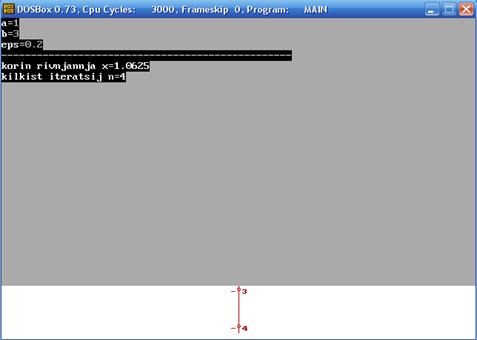
Рисунок 4.4 - Вікно із запитом на введення даних
eps=0.000001
-------------------------------------------------
korin rivnjannja 1.0625
kilkist iteratsij 4
a=-0.5
b=0.6
eps=0.000001
-------------------------------------------------
korin rivnjannja -2.14577e-07
kilkist iteratsij 21
Спробуємо збільшити точність:
a=-2
b=-1
eps=0.0000001
-------------------------------------------------
korin rivnjannja -1.42167
kilkist iteratsij 24
Як бачимо, кількість ітерацій зросла.
Перевіримо, чи записано у файл проміжні результати:
|
|
Дані записано нормально.
Після отримання числових результатів натискаємо довільну кнопку і переходимо до наступного вікна (рисунок 4.5), яке демонструє графічно реалізацію метода.
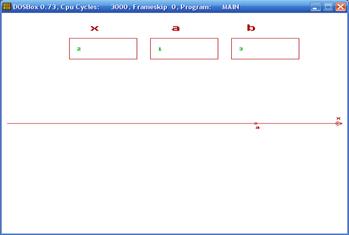
Рисунок 4.5 - Вікно демонстрації реалізації метода дихотомії
Дані для x, a та b завантажуються з текстових файлів KORENI.TXT та MEGI.TXT, точки будуються відповідно до цих даних. Після кожного натиснення будь-якої клавіші зчитуються наступні дані, аж поки не знайдемо значення x із заданою точністю.
Після натискання довільної кнопки переходимо до меню користувача (рисунок 4.6).
При вибору пунктів меню з’являються знайомі нам вже вікна:
1 - Рисунок 4.2;
2 - Рисунок 4.3;
3 або 5 - Рисунок 4.4;
4 - Рисунок 4.5.
Натиснувши 7 – вийдемо з програми, а обравши 6 побачимо вікно з інформацією про автора програми (Рисунок 4.7). На інші кнопки програма не реагує.
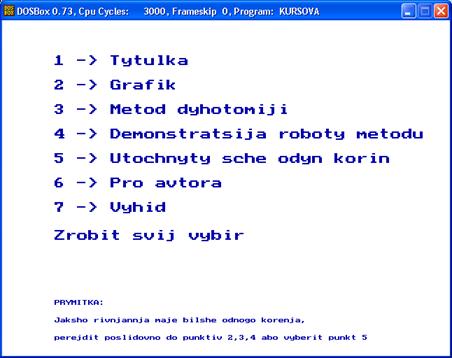
Рисунок 4.6 - Вікно меню користувача

Рисунок 4.7 - Вікно з інформацією про автора програми
Натиснувши довільну кнопку знову переходимо до вікна меню користувача.
5. ІНСТРУКЦІЯ КОРИСТУВАЧА
Для запуску програми потрібно зайти в папку Program і запустити на виконання файл kursova.exe. Для вірної роботи програми у тій же папці має бути файл-драйвер EGAVGA.bgi.
Дана програма може працювати під управлінням операційної системи сімейства Windows, починаючи від версії 95 та під управлінням ОС MS-DOS.
Мінімальні системні вимоги для коректної роботи програми:
- операційна система сімейства Windows або MS-DOS;
- процесор – не менше 80386;
- оперативної пам’яті – 1 Мб;
- відеокарта з якістю кольоропередачі – 16 біт;
- вільного місця на жорсткому диску – 135 кб.
Після запуску програми спочатку бачимо зображення електронної титульної сторінки (рисунок 4.2). Програма чекає, поки буде натиснута довільна кнопка. Що ми і робимо. З’являється графік функцій (рисунок 4.3). Знову натискаємо довільну кнопку. З’являється вікно із запитом на введення даних (рисунок 4.4). Вводимо послідовно значення межі проміжка та похибки. Отримаємо результати: корінь рівняння та кількість ітерацій.
Після отримання числових результатів натискаємо довільну кнопку і переходимо до наступного вікна (рисунок 4.5), яке демонструє графічно реалізацію метода. Дані для x, a та b завантажуються з текстових файлів KORENI.TXT та MEGI.TXT, точки будуються відповідно до цих даних. Після кожного натиснення будь-якої клавіші зчитуються наступні дані, аж поки не знайдемо значення x із заданою точністю. Після натискання довільної кнопки переходимо до меню користувача (рисунок 4.6).
При вибору пунктів меню з’являються знайомі нам вже вікна:
1 - Рисунок 4.2;
2 - Рисунок 4.3;
3 або 5 - Рисунок 4.4;
4 - Рисунок 4.5.
Натиснувши 7 – вийдемо з програми, а обравши 6 побачимо вікно з інформацією про автора програми (Рисунок 4.7). На інші кнопки програма не реагує. Натиснувши довільну кнопку знову переходимо до вікна меню користувача.
ВИСНОВКИ
В ході виконання даної курсової роботи ми вдосконалили свої знання мови С++ та вміння нею користуватися в середовищі Borland C++. Певна частина теоретичного матеріалу була опрацьована самостійно, використовуючи літературні джерела, а також інформаційні ресурси Інтернету. Серед новизни слід відмітити використання багатомодульного проектування.
Серед недоліків програми слід відмітити недостатність у візуальному оформленні, хоча середовище програмування і не дає широких можливостей для цього. Серед переваг помічаємо такі характеристики програми, як швидкодія, легкість у користуванні та невеликі розміри виконавчого файлу..
Створена нами програма проста та інтуїтивно зрозуміла і легка у користуванні.
У пояснювальній записці вповні розглянута проблема пошуку коренів нелінійних рівнянь, наведені необхідні формули та теореми. Крім того, побудовані блок-схеми алгоритмів основних функцій відповідають діючим стандартам і вимогам.
Отже, можемо зробити висновок, що створений нами проект повністю відповідає завданню, а пояснююча записка написана з дотриманням всіх вимог і стандартів.
ПЕРЕЛІК ПОСИЛАНЬ
1. Глинський Я.М., Анохін В.Є., Ряжська В.А. С++ і С++ Builder. Навч. посібн. 3-тє вид. – Львів: СПД Глинський, 2006. – 192с.
2. Пахомов Б.И. С/С++ и Borland C++ Builder для студента. – Спб.: БХВ-Петербург, 2006. – 448 с.:ил.
3. С/С++. Программирование на языке высокого уровня / Т.А. Павловская. СПб.: Питер, 2002. – 464 с
4. Сборник часто задаваемых вопросов и ответов к ним по компиляторам языков Си и C++ http://soft.munic.msk.su/
5. Уоррен Г.С. Алгоритмические трюки для программистов. - М.: Изд.дом «Вильямс», 2003
6. Шилдт Г. Теория и практика С++. — СПб.: BHV, 1996.
Додаток А.
(обов’язковий)
Загальна схема проекту.

Додаток Б.
(обов’язковий)
Текст програми
main.cpp
#include <stdlib.h>
#include <iostream.h>
#include <conio.h>
#include <graphics.h>
#include <dos.h>
#include <stdio.h>
#include <math.h>
#include "tytulka.cpp"
#include "grafik.cpp"
#include "dyhotom.cpp"
#include "demon.cpp"
void avtor()
{
clrscr();
setcolor(10);
int xmax=getmaxx(),ymax=getmaxy();
bar(0,0,xmax,ymax);
setcolor(BLUE);
settextstyle(0,0,2);
outtextxy(175,150,"Kursovu robotu");
outtextxy(230,250,"vykonav");
outtextxy(150,350,"Shypuk Oleksandr");
getch();
}
//===============================================================
void main()
{
clrscr();
int gdriver = DETECT, gmode, errorcode;
initgraph(&gdriver, &gmode,"");
errorcode = graphresult();
if (errorcode != grOk)
{
cout<< "ERROR" << grapherrormsg(errorcode);
cout<< "\n Press any key...";
getch();
exit(1);
}
tytulka();
grafik();
dyhotom();
demon();
int k=0;
while (k!=7)
{
setcolor(10);
int xmax=getmaxx(),ymax=getmaxy();
bar(0,0,xmax,ymax);
setcolor(BLUE);
settextstyle(0,0,2);
outtextxy(75,50,"1 -> Tytulka");
outtextxy(75,85,"2 -> Grafik");
outtextxy(75,120,"3 -> Metod dyhotomiji");
outtextxy(75,155,"4 -> Demonstratsija roboty metodu");
outtextxy(75,190,"5 -> Utochnyty sche odyn korin");
outtextxy(75,225,"6 -> Pro avtora");
outtextxy(75,260,"7 -> Vyhid");
outtextxy(75,300,"Zrobit svij vybir");
settextstyle(0,0,1);
outtextxy(75,400,"PRYMITKA:");
outtextxy(75,425,"Jaksho rivnjannja maje bilshe odnogo korenja,");
outtextxy(75,450,"perejdit poslidovno do punktiv 2,3,4 abo vyberit punkt 5");
cin>>k;
switch (k)
{
case 1: tytulka(); break;
case 2: grafik(); break;
case 3: dyhotom(); break;
case 4: demon(); break;
case 5: dyhotom(); break;
case 6: avtor(); break;
case 7: exit(1); break;
}
}
closegraph();
}
demon.cpp
#include <stdlib.h>
#include <iostream.h>
#include <conio.h>
#include <graphics.h>
#include <dos.h>
#include <stdio.h>
#include <math.h>
void demon()
{
int xmax=getmaxx(),ymax=getmaxy();
FILE *fp1,*fp2;
float x, a, b;
int i = 7;
char *buf;
buf = (char*)malloc(5);
fp1=fopen("koreni.txt","rt");
fp2=fopen("megi.txt","rt");
while (!feof(fp1))
{
clrscr();
fscanf(fp1,"%f\n",&x);
fscanf(fp2,"%f\n",&a);
fscanf(fp2,"%f\n",&b);
setcolor(WHITE);
bar(0,0,xmax,ymax);
setcolor(RED);
settextstyle(0,0,2);
outtextxy(165,25,"x");
outtextxy(315,25,"a");
outtextxy(455,25,"b");
rectangle(125,55,250,100);
rectangle(275,55,400,100);
rectangle(425,55,550,100);
settextstyle(0,0,1);
setcolor(GREEN);
gcvt(x,i,buf);
outtextxy(140,75,buf);
gcvt(a,i,buf);
outtextxy(290,75,buf);
gcvt(b,i,buf);
outtextxy(440,75,buf);
setcolor(RED);
line(10,240,630,240);
line(620,235,630,240);
line(620,245,630,240);
settextstyle(0,0,1);
outtextxy(620,225,"x");
circle(20+(x+2)*150,240,2);
outtextxy(20+(x+2)*150,225,"x");
circle(20+(a+2)*150,240,2);
outtextxy(20+(a+2)*150,245,"a");
circle(20+(b+2)*150,240,2);
outtextxy(20+(b+2)*150,255,"b");
getch();
free(buf);
}
}
dyhotom.cpp
#include <stdlib.h>
#include <iostream.h>
#include <conio.h>
#include <graphics.h>
#include <dos.h>
#include <stdio.h>
#include <math.h>
double f(double x)
{
return x*x*x/3-atan(x);
}
//===============================================================
void dyhotom()
{
clrscr();
FILE *fp1,*fp2;
fp1=fopen("koreni.txt","wt");
fp2=fopen("megi.txt","wt");
int k=0;
double a, b, c, epsilon;
cout << "a=";
cin >> a;
cout << "b=";
cin >> b;
cout << "eps=";
cin >> epsilon;
if (f(a)*f(b)>0)
cout << "nemaje koreniv abo bilshe odnogo na tsjomu promizhku" << endl;
else
{
while (b - a > epsilon)
{
c = (a + b) / 2;
fprintf(fp1,"%f\n",c);
fprintf(fp2,"%f\n",a);
fprintf(fp2,"%f\n",b);
if(f(c)==0) break;
if(f(b) * f(c) < 0)
a = c;
else
b = c;
k++;
}
cout << "-------------------------------------------------" << endl;
cout << "korin rivnjannja x=" << (a + b) / 2 << endl;
cout << "kilkist iteratsij n=" << k << endl;
}
fclose(fp1);
fclose(fp2);
getch();
}
grafik.cpp
#include <stdlib.h>
#include <iostream.h>
#include <conio.h>
#include <graphics.h>
#include <dos.h>
#include <stdio.h>
#include <math.h>
void grafik()
{
clrscr();
setcolor(WHITE);
int xmax=getmaxx(),ymax=getmaxy();
bar(0,0,xmax,ymax);
setcolor(RED);
line(10,240,630,240);
line(620,235,630,240);
line(620,245,630,240);
settextstyle(0,0,1);
outtextxy(620,225,"x");
line(320,10,320,470);
line(320,10,315,20);
line(320,10,325,20);
outtextxy(330,10,"y");
int dec, sign;
int i;
for (i=-2;i<=2;i++)
{
circle(20+((i+2)*150),240,2);
if(i>0)
outtextxy(17+((i+2)*150),250,fcvt(i, 0, &dec, &sign));
else if(i<0)
{
outtextxy(17+((i+2)*150),250,fcvt(i, 0, &dec, &sign));
outtextxy(10+((i+2)*150),250,"-");
}
else outtextxy(25+((i+2)*150),250,fcvt(i, 0, &dec, &sign));
}
for (i=-4;i<=4;i++)
{
circle(320,20+(4+i)*55,2);
if(i<0)
outtextxy(325,20+(4+i)*55,fcvt(-i, 0, &dec, &sign));
else if (i>0)
{
outtextxy(325,20+(4+i)*55,fcvt(-i, 0, &dec, &sign));
outtextxy(310,20+(4+i)*55,"-");
}
}
setcolor(BLUE);
float x1,x2,y1,y2,xx1,xx2,yy1,yy2;
x1=-2;y1=atan(x1);
for (x2=-2;x2<=2;x2+=0.01)
{
y2=atan(x2);
xx1=20+(x1+2)*150;
xx2=20+(x2+2)*150;
yy1=460-(y1+4)*55;
yy2=460-(y2+4)*55;
line(xx1,yy1,xx2,yy2);
x1=x2;y1=y2;
}
outtextxy(520,210,"y(x)=atan(x)");
setcolor(GREEN);
x1=-2;y1=x1*x1*x1/3;
for (x2=-2;x2<=2;x2+=0.01)
{
y2=x2*x2*x2/3;
xx1=20+(x1+2)*150;
xx2=20+(x2+2)*150;
yy1=460-(y1+4)*55;
yy2=460-(y2+4)*55;
line(xx1,yy1,xx2,yy2);
x1=x2;y1=y2;
}
outtextxy(480,120,"y(x)=x*x*x/3");
getch();
}
tytulka.cpp
#include <stdlib.h>
#include <iostream.h>
#include <conio.h>
#include <graphics.h>
#include <dos.h>
#include <stdio.h>
void tytulka()
{
clrscr();
setcolor(WHITE);
int a=5,xmax=getmaxx(),ymax=getmaxy();
bar(0,0,xmax,ymax-3*a);
setcolor(GREEN);
rectangle(2*a,a,xmax-a,ymax-4*a);
settextstyle(0,0,1);
outtextxy(190,15,"Ministerstvo osvity i nauky Ukrainy");
outtextxy(160,30,"Lutskij natsionalnyj tehnichnyj universytet");
outtextxy(350,65,"Kafedra kompjuternoji inzheneriji");
setcolor(RED);
settextstyle(0,0,2);
outtextxy(200,190,"Kursova robota");
settextstyle(0,0,1);
outtextxy(265,215,"z dyscypliny");
outtextxy(255,235,"PROGRAMUVANNJA");
outtextxy(280,250,"na temu: ");
outtextxy(120,265,"ROZVJAZUVANNJA NELINIJNYH RIVNJAN METODOM DYHOTOMIJI ");
setcolor(GREEN);
outtextxy(350,350,"Vykonav st.gr.KSMS-13");
outtextxy(350,365,"Kostenko Vasyl");
outtextxy(350,380,"Pereviryv asystent");
outtextxy(350,395,"Lavrenchuk S.V.");
outtextxy(275,445,"Lutsk 2010");
setcolor(RED);
outtextxy(260,470,"Press any key... ");
getch();
}
Додаток В
(обов’язковий)
Блок-схеми алгоритмів
void avtor()
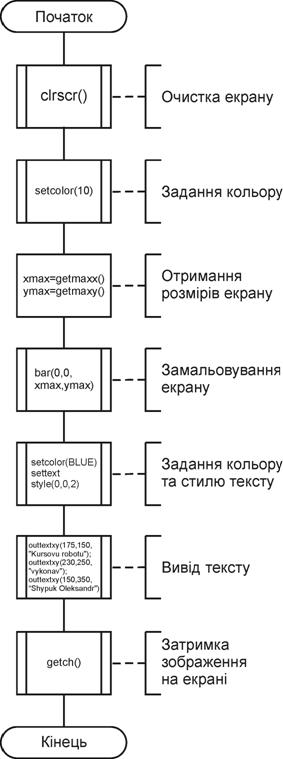

void main()
void grafik()

void dyhotom()

Похожие работы
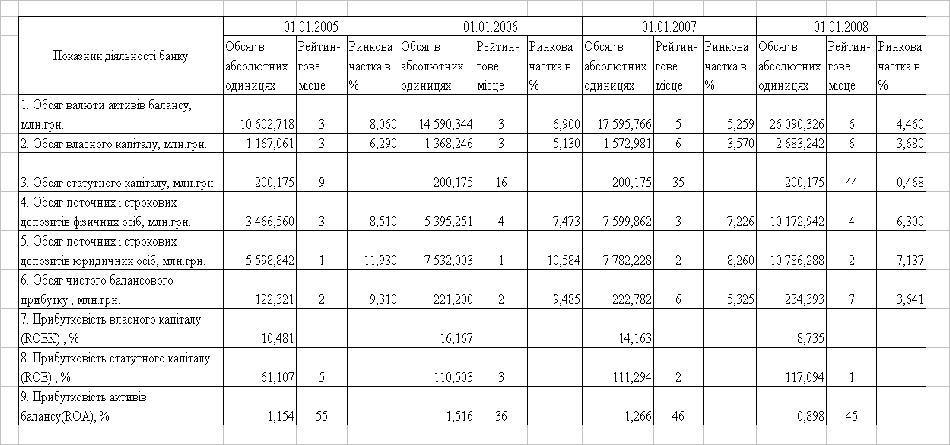
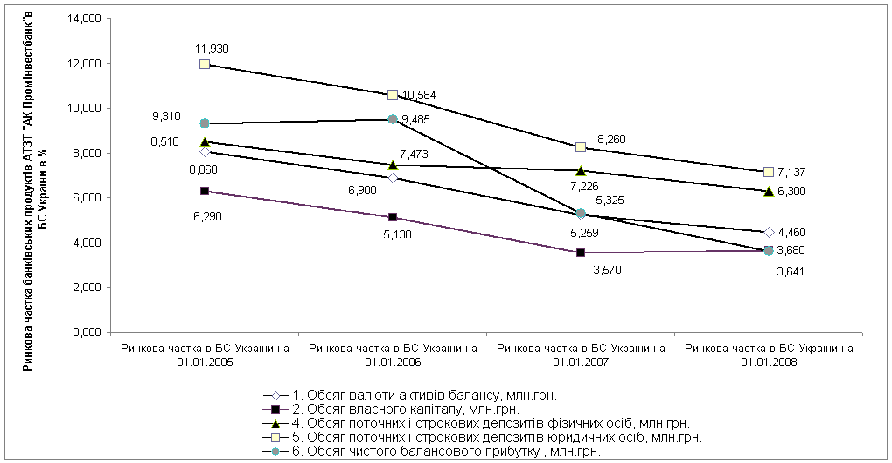
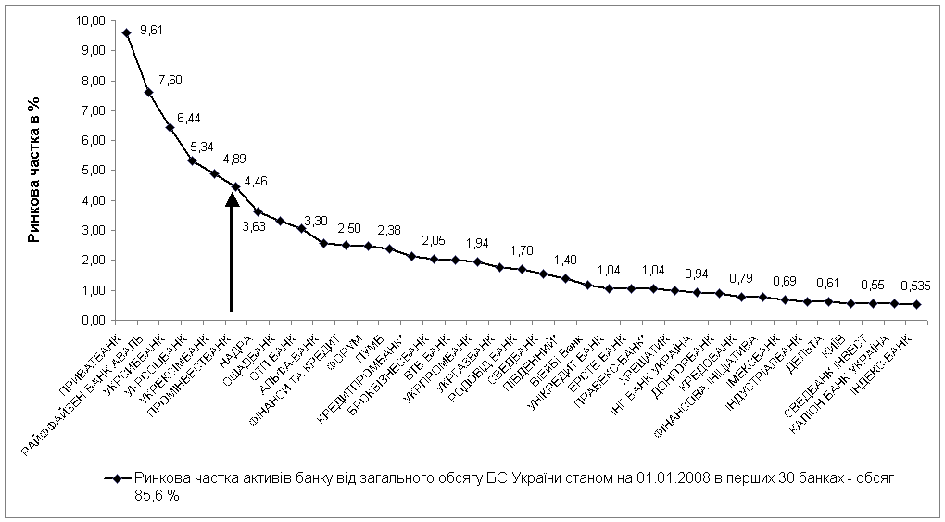
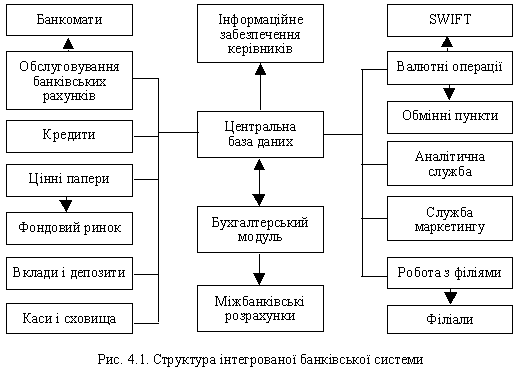
... В АБС АКБ «ПРОМІНВЕСТБАНК» ТА ОЦІНКА РІВНЯ ВРАЗЛИВОСТІ БАНКІВСЬКОЇ ІНФОРМАЦІЇ 3.1 Постановка алгоритму задачі формування та опис елементів матриці контролю комплексної системи захисту інформації (КСЗІ) інформаційних об’єктів комерційного банку В дипломному дослідженні матриця контролю стану побудови та експлуатації комплексної системи захисту інформації в комерційному банку представлена у вигляді ...
... – відпускна ціна i-го заводу j-й продукції; - закупівельна ціна i-го заводу j-й продукції, - шуканий обсяг закупівель на i-м заводі j-й продукції. 2.5 Перевірка моделі оптимізації на контрольному прикладі В цьому підрозділі на прикладі підприємства ТОВ "Гермес-Груп" розрахуємо модель (2.4.5) за допомогою електроних таблиць MSEcxel. Цільова функція має вигляд: де - об’єм закупівлі; ...
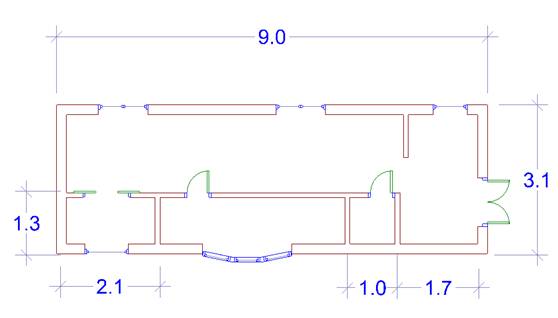
к само даних про споживання електричної енергії, опис можливої діяльності офісу і працівниках. 1 ГРАФІЧНЕ МОДЕЛЮВАННЯ ОФІСУ САПР-ОДЯГ 1.1 Початкові дані для проектування офісу Вихідні дані: Діяльність офісу САПР - одяг Кількість комп'ютерів 2 Кількість принтерів 2 Блоки безперебійного живлення 2 Кількість сканерів 1 Модем + Телевізор (підключення до ЕОМ) + ...
... Перевірка гіпотез; - Формулювання понять, узагальнень, висновків; - Впровадження висновків. На сьогодні існують кілька національних, регіональних і міжнародних програм, які впроваджують використання нових інформаційних технологій для створення різноманітних проектів, у яких беруть участь учні й вчителя середніх шкіл. Це такі програми як EuroSchoolNet, Orilla Orilla, GLOBE. Висновок ...








0 комментариев