Навигация
Знаходження характеристик вибіркового розподілу
3.2 Знаходження характеристик вибіркового розподілу
При статистичній обробці експериментальних даних випадкової величини X знаходять оцінки числових характеристик, які найбільш часто зустрічаються, себто математичного сподівання і дисперсії:
1) ![]() - математичне сподівання (вибіркове середнє);
- математичне сподівання (вибіркове середнє);
2)  - виправлена (незміщена) дисперсія;
- виправлена (незміщена) дисперсія;
3) ![]() - середньоквадратичне відхилення.
- середньоквадратичне відхилення.
Розглянуті оцінки називаються точковими, так як вони визначаються одним числом, зображеним точкою на числовій осі. Але при малому об’ємі вибірки точкова оцінка ![]() може значно відрізнятися від оцінюваного параметру а. Тому у ряді задач матстатистики вимагається знайти не тільки параметр а, але його точність та надійність.
може значно відрізнятися від оцінюваного параметру а. Тому у ряді задач матстатистики вимагається знайти не тільки параметр а, але його точність та надійність.
Для визначення точності оцінки ![]() в матстатистиці користуються надійним інтервалом, а для визначення надійності - надійною ймовірністю.
в матстатистиці користуються надійним інтервалом, а для визначення надійності - надійною ймовірністю.
Нехай для параметра а одержана із досліду незсунена оцінка ![]() . Ми хочемо оцінити можливу при цьому помилку. Задаємо деяку велику ймовірність g (наприклад, g=0,9; 0,95; 0,99; ...) таку, щоб подію з ймовірністю g можна було б вважати практично вірогідною, і знайдемо таке значення d>0, для якого
. Ми хочемо оцінити можливу при цьому помилку. Задаємо деяку велику ймовірність g (наприклад, g=0,9; 0,95; 0,99; ...) таку, щоб подію з ймовірністю g можна було б вважати практично вірогідною, і знайдемо таке значення d>0, для якого
![]() (3.1)
(3.1)
Подамо (1) у вигляді міри довіри
![]() (3.2)
(3.2)
Рівність (2) показує, що невідомі значення параметра а з ймовірністю b попадають у інтервал ![]() (3.3)
(3.3)
Відмітимо, що тут невідоме значення параметра а являється випадковою величиною, а інтервал lg і випадковою величиною, так як положення інтервалу на вісі залежить від в.п. ![]() (центр інтервалу), довжина також у загальному випадку являється випадковою величиною. Тому ймовірність g у даному випадку тлумачать не як ймовірність попадання випадкової величини а в інтервал lg , а як ймовірність того, що випадковий інтервал lg накриває точку а.
(центр інтервалу), довжина також у загальному випадку являється випадковою величиною. Тому ймовірність g у даному випадку тлумачать не як ймовірність попадання випадкової величини а в інтервал lg , а як ймовірність того, що випадковий інтервал lg накриває точку а.
![]()
Рисунок 4 - Надійний інтервал ![]()
Інтервал lg (рис. 4) називається надійним інтервалом, а b - надійною ймовірністю або надійністю. Розглянемо приклад знаходження надійного інтервалу для математичного сподівання.
Треба побудувати надійний інтервал lg, що відповідає надійній ймовірності g, для математичного сподівання в.в. Х.
Для цього користуються формулою ![]() . (3.4) Зміст співвідношення (4): з надійністю b можна стверджувати, що надійний інтервал
. (3.4) Зміст співвідношення (4): з надійністю b можна стверджувати, що надійний інтервал ![]() накриває невідомий параметр mx; точність оцінки
накриває невідомий параметр mx; точність оцінки ![]() .
.
Отже, поставлена вище задача розв’язана. З рівності ![]() або
або ![]() по таблиці функції Лапласа
по таблиці функції Лапласа ![]() знаходимо аргумент t, якому відповідає значення функції Лапласа
знаходимо аргумент t, якому відповідає значення функції Лапласа ![]() .
.
Також необхідно провести групування і побудову гістограми для Lкр, а також з’ясувати чи розподілена дана в.в. за нормальним законом за допомогою критерію Пірсона.
При великому числі дослідів статистичний матеріал, вміщений у таблицю важко аналізувати. Тому на основі одержаних даних складається групування або інтервальний варіаційний ряд. Робиться це наступним чином.
Увесь інтервал, одержаних значень хі розбивають на часткові інтервали (як правило рівні): (х1,х2), (х2,х3), ..., (хm+1,хm) і підраховують число nі величини Х, яка попала в інтервал (хі,хі+1). Значення, які попали на кінець інтервалу, відносять або до правого, або до лівого інтервалу (хі,хі+1). Відмітимо, що ![]() . На основі результатів обробки дослідів будуємо таблицю 2, що є групуванням або інтервальний варіаційний ряд.
. На основі результатів обробки дослідів будуємо таблицю 2, що є групуванням або інтервальний варіаційний ряд.
| Ii | (х1,х2) | (х2,х3) | ... | (хk,хk+1) |
| ni | n1 | n2 | ... | nk |
| pi* | p1* | p2* | ... | pk* |
Відкладемо на вісі ОХ точки х1, х2, х3, ..., хk, хk+1, ... , хm. На відрізку [хі, хі+1] як на основі будуємо прямокутник, площа якого дорівнює рі*. Із способу побудови гістограми випливає, що повна площа її дорівнює 1.
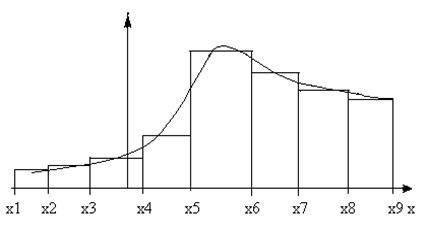 |
Рисунок 5 - Гістограма і графік щільності випадкової величини Х
Очевидно, що при збільшенні числа дослідів можна вибирати все більше і більше дрібні інтервали. При цьому гістограма (рис. 5) все більше і більше наближатиметься до деякої кривої, що обмежує площу рівну одиниці. Неважко бачити, що крива уявляє собою графік щільності випадкової величини Х.
Критерій Пірсона для перевірки гіпотези про нормальний розподіл обчислюється наступним чином:
![]() ,
,
де ![]() - теоретичні частоти, що обчислюються як
- теоретичні частоти, що обчислюються як ![]() ;
; ![]() - емпіричні частоти;
- емпіричні частоти;
![]() - кількість інтервалів варіаційного ряду.
- кількість інтервалів варіаційного ряду.
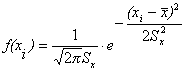 - функція щільності для нормального закону.
- функція щільності для нормального закону.
Якщо ![]() , то гіпотеза приймається, в противному разі - відкидається.
, то гіпотеза приймається, в противному разі - відкидається.
Похожие работы
... і успіхові реформ, в Україні пішли хибним шляхом перерозподілу національного багатства на користь незначного прошарку так званих "нових українців". 2. Інвестиційна діяльність в ринковій економіці Сьогодні у складній та заплутаній системі економічних зв’язків все частіше необхідно приймати зважені рішення щодо накопичення та інвестування. Для збереження і примноження заощаджень потрібно ві ...

0 комментариев