Спосіб (шляхом «переміщення» кожного елемента списку, починаючи з другого, на його початок)

1 спосіб (шляхом «переміщення» кожного елемента списку, починаючи з другого, на його початок)

Зауваження! Під переміщенням елемента розуміємо не фізичне переміщення його на початок списку. На початок списку «направляємо» лише вказівник елемента, який з даного списка видаляється.

S_1 – вказівник на перший елемент списку

S – вказівник на поточний елемент списку

Buf – вказівник на наступний за поточним елементом (на елемент що переміщається на початок списку

s:=s_1;

buf:=s_1;

while s^.next<>nil do

begin

buf:=s^.next;

s^.next:=s^.next^.next;

buf^.next:=s_1;

s_1:=buf;

end;

2 спосіб (шляхом зміни напрямків вказівників на протилежний)

S_1 – вказівник на перший елемент списку

S – вказівник на поточний елемент списку

Left – вказівник на елемент, що знаходиться лівіше від поточного

Right – вказівник на елемент, що знаходиться правіше від поточного

right:=s_1;

s:=nil;

repeat

left:=s;

s:=right;

right:=right^.next;

s^.next:=left;

until right=nil;

РОЗДІЛ ІІ. ДЕРЕВА. БІНАРНЕ ДЕРЕВО

Деревом називається динамічна структура, у якій кожен вузол містить не один, а декілька вказівників на декілька інших вузлів.

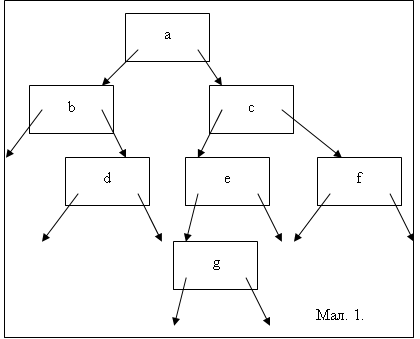Кореневий вузол (корінь дерева) – це самий верхній вузол (вузол a – кореневий) . Якщо з деякого вузла (наприклад, вузла а) вказівники вказують на інші вузли (в нашому випадку на вузли b та c), то такий вузол називають предком. Вузли ж на які вказують вказівники від предка називаються потомками.

Все сказане вище ілюструє малюнок 1, якщо його розглянути то можна зробити висновки про те, що:

·          Лівий потомок вузла а – вузол b

·          Правий потомок – вузол c.

·          Вузли b та c мають спільного предка – вузол а

Якщо вузол не має потомків, то такий вузол називають листком дерева, тому згідно малюнка вершини d, g та f – є листками.

 Дерево, кожен вузол якого не може мати більше двох потомків називається бінарним.

 

2.1. РЕАЛІЗАЦІЯ БІНАРНОГО ДЕРЕВА ЗА ДОПОМОГОЮ ДИНАМІЧНИХ ЗМІННИХ

Розглянемо динамічну змінну b, що має таку структуру, як показано на малюнку 2. А саме, змінна b є записам з 5 полів:

Parent –вказівник на предка

Left – вказівник на лівого потомка

Right – вказівник на правого потомка

Data – поле даних (наприклад, прізвище)

Key – ключ (цілочисельне значення), по якому ідентифікується елемент.

Тип такої динамічної змінної виглядає наступнич чином:

type

BinarTree=^node;

node=record

key:integer;

data:string;

left,right,
parent:BinarTree;

end;

Сформуємо дерево керуючись таким принципом: ключ кожного лівого потомка менший за ключ предка, а ключ правого потомка – більший або рівний ключа предка.

Наприклад, бінарне дерево з трьох вузлів (Іванов (ключ=5), Петров (ключ=3) та Сидоров (ключ=8)) має вигляд як показано на мал.3. Добавимо в дерево елемент Ільїн з ключем 6. Цей елемент буде лівим потомком елемента Сидоров (так як 6>5 та 6<8). Якби ключ елемента Ільїн був рівний 4, то він був би правим потомком елемента Петров (бо 4<5 та 4>3)

При вставці кожного наступного елемента (нехай вказівник b_new вказує на цей елемент) в дерево (b вказує на корінь цього дерева), ми повинні спочатку знайти листок (нехай на нього вказує вказівник b_parent), який буде предком елемента що вставляєть.

Для пошуку такого листка використаємо деякий проміжний вказівник b_buf, який спочатку буде вказувати на корінь дерева b, а потім крок за кроком приймати значення b_buf^.left або b_buf^.right в залежності від значенні ключа елемента що вставляється (b_new) до тих пір, поки не дойде до листка дерева.

Програмний код пошуку елемента b_parent.

b_buf:=b;

while b_buf<>nil do

begin
b_parent:=b_buf;
if b_new^.key<b_parent^.key
then b_buf:=b_buf^.left

else b_buf:=b_buf^.right;

end;

Наступний крок – направити вказівник b_new^.parent на знайдений елемент b_parent та вказівники left або right знайденого елемента b_parent на елемент, що вставляється b_new:

Програмний код виставлення лівого та правого вказівників знайденого елемента-предка (b_parent^.left та b_parent^.right) на новий елемент (b_new) та вказівника нового елемента-потомка (b_new^.parent) на знайдений елемент-предок (b_parent):

b_new^.parent:=b_parent;if b_new^.key<b_parent^.key then b_parent^.left:=b_new

else b_parent^.right:=b_new

ВИВЕДЕННЯ НА ЕКРАН ЛИСТКІВ БІНАРНОГО ДЕРЕВА.

Процедура виведення листів бінарного дерева є рекурсивною. Адже листками деякого дерева Х є листи його лівого та правого потомків (якщо ці потомки не nil). Назвемо процедуру виведення листка дерева write_tree(x:BinarTree). Якщо лівий та правий вказівники деякого елемента вказують на nil значить цей елемент є листом, а отже його треба вивести на екран. Інакше шукаємо листки лівого потомка (якщо він не рівний nil), а потім – правого потомка (якщо він також не рівний nil).

procedure write_tree(x:BinarTree);

begin

if (x^.left=nil) and (x^.right=nil) then write(x^.data,' ')

else

begin

if x^.left<>nil then write_tree(x^.left);

if x^.right<>nil then write_tree(x^.right);

end;

end;

ТЕКСТ ПРОГРАМИ ФОРМУВАННЯ БІНАРНОГО ДЕРЕВА
ТА ВИВЕДЕННЯ НА ЕКРАН ЙОГО ЛИСТІВ

 

uses crt;

type

BinarTree=^node;

node=record

key:integer;

data:string;

left,right,parent:BinarTree;

end;

var

b,b_parent,b_new,b_buf:BinarTree;

name:string;

k:integer;

procedure write_tree(x:BinarTree);

begin

if (x^.left=nil) and (x^.right=nil) then write(x^.data,' ')

else

begin

if x^.left<>nil then write_tree(x^.left);

if x^.right<>nil then write_tree(x^.right);

end;

end;

begin

clrscr;

repeat

write('Фамилия -> ');

readln(name);

if name<>'' then

begin

write('Ключ -> ');

readln(k);

new(b_new);

with b_new^ do

begin

parent:=nil;

left:=nil;right:=nil;

data:=name;

key:=k;

end;

if b=nil then b:=b_new

else

begin

b_buf:=b;

while b_buf<>nil do

begin

b_parent:=b_buf;

if b_new^.key<b_parent^.key then b_buf:=b_buf^.left

else b_buf:=b_buf^.right;

end;

b_new^.parent:=b_parent;

if b_new^.key<b_parent^.key then b_parent^.left:=b_new

else b_parent^.right:=b_new

end;

end;

until name='';

write('Листы дерева: ');

write_tree(b);

writeln;

end.

Результат роботи програми:

Имя -> Иванов

Ключ -> 5

Имя -> Петров

Ключ -> 3

Имя -> Сидоров

Ключ -> 8

Имя -> Ильин

Ключ -> 6

Имя ->

Листі дерева: Петров Ильин

ВИВЕДЕННЯ НА ЕКРАН УСІХ ВУЗЛІВ БІНАРНОГО ДЕРЕВА

 

Видозмінимо процедуру виведення листів бінарного дерева в процедуру виведення усіх його вузлів: лівий потомок - правий потомок – предок - … - кореневий вузол:

procedure write_tree(x:BinarTree);

begin

 if (x^.left<>nil) or (x^.right<>nil) then

 begin

if x^.left<>nil then write_tree(x^.left);

if x^.right<>nil then write_tree(x^.right);

 end;

 write(x^.data,' ');

end;

Тут виведення вузлів здійснюється як результат зворотньої дії рекурсивної процедури (вказівка write(x^.data,' ') – вкінці процедури). При такій організації вузли розпочнуть виводитись на екран після досягнення крайнього лівого листка.

При введенні бінарного дерева, зображеного на малюнку 4, результат роботи описаної процедури буде наступним:

Все узлы дерева: 0 2 1 4 5 3 7 9 8 6 11 13 12 15 18 20 19 17 16 14 10

Якщо вказівку write(x^.data,' ') розмістити не в кінці, а на початку процедури, то виведення вузлів буде здійснюватися як результат прямої дії рекурсії. Тобто, спочатку виведуться усі ліві потомки кореня дерева, потім правий потомок предка крайнього лівого листка і всі його ліві потомки і т.д. аж до крайнього правого лиска дерева.

В цьому випадку при введенні того ж дерева (мал.4) результат роботи такої процедури наступний:

Все узлы дерева: 10 6 3 1 0 2 5 4 8 7 9 14 12 11 13 16 15 17 19 18 20

ВИЗНАЧЕННЯ КІЛЬКОСТІ РІВНІВ БІНАРНОГО ДЕРЕВА (ВИСОТИ ДЕРЕВА)

 

На малюнку 5 зображено шести-рівневе бінарне дерево. Лівий потомок (6) – 4-х рівневе дерево. Правий потомок (16) 5-ти рівневе дерево. Бачимо, що для того, щоб визначити висоту дерева необхідно до висоти «вищого» потомка додати 1. Виходячи з таких міркування функція визначення висоти дерева (Function height_tree(x:BinarTree):integer) має рекурсивний характер.

Нехай i – висота лівого потомка, а j – висота правого потомка. Тоді:

Function height_tree(x:BinarTree):integer;

var

i,j:integer;

begin

if x=nil then height_tree:=0

else

begin

i:=height_tree(x^.left);

j:=height_tree(x^.right);

if i>j then height_tree:=i+1

else height_tree:=j+1;

end;

end;

При введенні дерева, зображеного на мал.5, результат роботи функції height_tree наступний:

Висота дерева: 6

ВИСНОВКИ

У виконаній роботі було розглянуто процеси пошуку інформацій та розроблено структури даних для ефективного зберігання та обробки інформації. Як приклад розглянуто бінарне дерево. Це динамічна структура даних, розмір якої обмежується тільки розміром віртуальної пам’яті комп’ютера. Бінарні дерева забезпечують пошук конкретного значення, максимуму, мінімуму, попереднього, наступного, операції вставки та видалення елемента.

Розглянуті у роботі бінарні структури широко використовуються у житті, наприклад це різноманітні "ієрархічні структури", які нині широко використовуються в багатьох комп'ютерних завданнях. На даний час також розвивається граматичний аналіз, в основі якого і знаходяться принципи бінарних дерев. Граматичний аналіз на даний час широко використовується у сучасних пошукових алгоритмах.

Тому вивчення бінарних дерев та їх функціонування має важливе значення.

СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ.

 

1.         Никита Культин «Программирование в Turbo Pascal и Delphi» — СПб.: БХВ — Санкт-Петербург, 1999.

2.         С.А.Немнюгин «Turbo Pascal: практикум» — СПб.: Питер, 2001.

3.         Е.А.Зуев «Программирование на языке Turbo Pascal 6.0., 7.0. — Москва: Веста, Радио и связь, 1993.

4.         Аляев Ю.А., Козлов О.А. Программирование. Pascal, C++, Visual Basic. М.: Финансы и статистика, 2004.

5.         Гуденко Д., Петроченко Д. Сборник задач по программированию. – Спб.: Питер, 2003.