Навигация
Добавить еще одно утверждение в продукционной модели, что если есть дорога из А в Б, то можно переехать не только из А в Б, но и из Б в А
1. Добавить еще одно утверждение в продукционной модели, что если есть дорога из А в Б, то можно переехать не только из А в Б, но и из Б в А.
2. Программно реализовать, чтобы система понимала, что наличие дороги означает, что можно переехать из А в Б, но и наооброт.
5. Описание программыОпределим отношение
path(A,Z,P,D),
где P - ациклический путь между вершинами A и Z в графе, представленном следующими дугами:
arca(a,b,1).
arca(a,c,1).
arca(b,e,1).
arca(b,d,1).
arca(c,d,1).
arca(c,g,1).
arca(c,f,1).
arca(d,e,1).
arca(e,f,1).
arca(f,x,1).
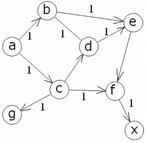
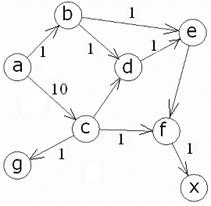
Дуги прописаны согласно рис.1.
Для реализации метода поиска выберем метод поиск в глубину, который основан на следующих соображениях:
Если A = Z, то положим P = [A];
Иначе нужно найти ациклический путь P1 из произвольной вершины Y в Z, а затем найти путь из A в Y, не содержащий вершин из P1.
Введем отношение
path1(A,P1,P,D),
означающее, что P1 - завершающий участок пути P.
Между path и path1 имеет место соотношение:
path(A,Z,P,D) :- path1(A,[Z],P,D).
Рекурсивное определение отношения path1 вытекает из следующих посылок:
"граничный случай": начальная вершина пути P1 совпадает с начальной вершиной A пути P;
в противном случае должна существовать такая вершина X, что: 1) Y - вершина, смежная с X, 2) X - не содержится в P1, 3) для P выполняется отношение path(A,[Y|P1],P).
Отношение можно реализовать согласно:
path(A,Z,Path,C):- path1(A,[Z],0,Path,C).
path1(A,[A|Path1],C,[A|Path1],C).
path1(A,[Y|Path1],C1,Path,C):- arca(X,Y,CXY),
not(member(X,Path1)),C2=C1+CXY,path1(A,[X,Y|Path1],C2,Path,C).
Где отношение member - определяет принадлежит ли элемент списку, реализованное следующим кодом:
member(Head,[Head|_]).
member(Head,[_|Tail]):- member(Head,Tail).
Для реализации выбора оптимального выбора (минимальная длина) среди перечня путей введем отношение db0 и db:
db0(X,Y) :-path(X,Y,P,C), assert(db_path(X,Y,P,C)).
db(X,Y):-db_path(X,Y,P,C), path(X,Y,MP,MC), MC<C,!,
retract(db_path(X,Y,P,C)), assert(db_path(X,Y,MP,MC)), db(X,Y).
Отношение db0 инициализирует первый возможный путь. Если данный путь не единичен, то db инициализирует следующий путь, и в то же время сравнивает длины двух данных путей. В процессе последующих рекурсий и сравнения остается только один путь, длина которого минимальна.
Текст программы:
domains
i=integer
s=symbol
list=s*
database
db_path(s,s,list,i)
predicates
path(s,s,list,i)
path1(s,list,i,list,i)
member(s,list)
arca(s,s,i)
db0(s,s)
db(s,s)
run(s,s)
start
goal
start.
clauses
start:-makewindow(1,7,7,"Expert System",1,3,22,71),clearwindow,
write("Enter the name of cities"),nl,
write("The first city: "), readln(First),nl,
write("The second city: "), readln(Second),nl,
run(First,Second),readchar(_).
arca (a,b,1).
arca(a,c,1).
arca(b,e,1).
arca(b,d,1).
arca(c,d,1).
arca(c,g,1).
arca(c,f,1).
arca(d,e,1).
arca(e,f,1).
arca(f,x,1).
run(Start,End):-db0(Start,End), db(Start,End), db_path(Start,End,MP,MD),
write("Optimum way: "),write(MP),nl,
write("Length of an optimum way="),write(MD),
nl,nl.
path(A,Z,Path,C):- path1(A,[Z],0,Path,C).
path1(A,[A|Path1],C,[A|Path1],C).
path1(A,[Y|Path1],C1,Path,C):- arca(X,Y,CXY), not(member(X,Path1)),C2=C1+CXY, path1(A,[X,Y|Path1],C2,Path,C).
member(Head,[Head|_]).
member(Head,[_|Tail]):- member(Head,Tail).
db0(X,Y) :-path(X,Y,P,C), assert(db_path(X,Y,P,C)).
db(X,Y):-db_path(X,Y,P,C), path(X,Y,MP,MC), MC<C,!,
retract(db_path(X,Y,P,C)), assert(db_path(X,Y,MP,MC)), db(X,Y).
db(_,_).
6. Тестирование программыа) Пусть имеем следующий граф:
|
|
|
| Рис.2 | Рис.2а |
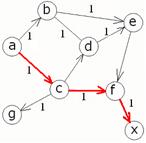
Ищем оптимальный путь из a в х, согласно графу оптимальный путь содержит следующие узлы: a c f x, что изображено на рис.2а.
Программа:
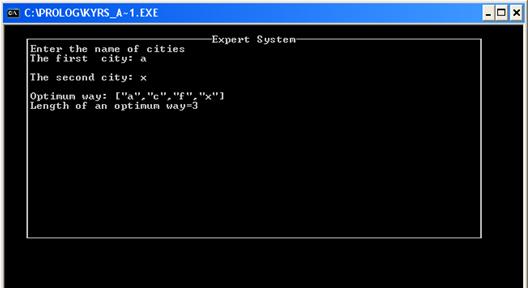
Данные ручного расчета и программы совпадают.
б) Изменим длину ребра a-c:
|
|
|
| Рис.3 | Рис.3а |
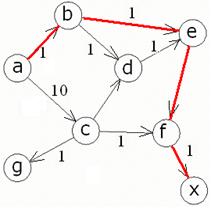
Ищем оптимальный путь из a в х, согласно графу оптимальный путь содержит следующие узлы: a b e f x, что изображено на рис.3а.
Программа:
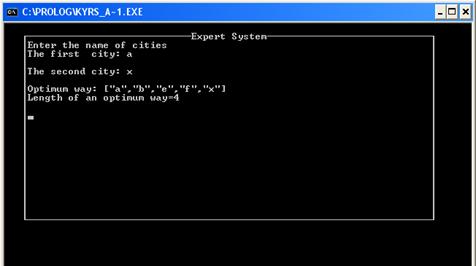
Данные ручного расчета и программы совпадают.
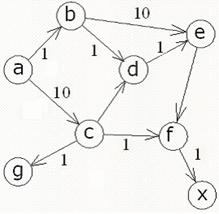
в) Изменим длину ребра b-d:
|
|
|
| Рис.4 | Рис.4а |
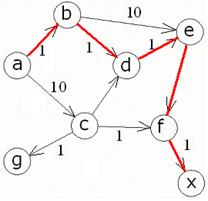
Ищем оптимальный путь из a в х, согласно графу оптимальный путь содержит следующие узлы: a b d e f x, что изображено на рис.4а.
Программа:

Данные ручного расчета и программы совпадают.
Литература
1. И 57. Использование Турбо-Пролога: Пер. с англ.-М.:Мир, 1990.-410 с., ил.
2. Б 87. Братко. Программирование на языке Пролог для искусственного интеллекта: Пер. с англ. -М.: Мир, 1990.- 560 с., ил
Похожие работы
... Architect, Visible Analyst Workbench, EasyCASE), так и новые версии и модификации перечисленных систем. 3 Глава. Разработка концептуальной модели информационной системы для поддержки принятия управленческих решений при формировании маркетинговой стратегии региона Процесс создания и внедрения любой ИС принято разделять на четыре последовательные фазы: анализ, глобальное проектирование ( ...
... . Реакции узлов более высокого уровня менее зависят от позиции и более устойчивы к искажениям. Структура Неокогнитрон имеет иерархическую структуру, ориентированную на моделирование зрительной системы человека. Он состоит из последовательности обрабатывающих слоев, организованных в иерархическую структуру (рис. 10.8). Входной образ подается на первый слой и передается через плоскости, ...
... условиях определенности математическое программирование дает точное решение поставленной задачи. Поэтому необходимости выбирать из нескольких вариантов попросту нет. Таким образом, в условиях определенности "Теория принятия решений" не используется, такими задачами занимается математическое программирование. 2) ЛПР знает вероятность реакции окружающей среды на выбор им той или иной альтернативы. ...
... и эксплуатацию подавляющего большинства ЛС. И этот факт предопределяет проблему прогнозирования затрат, цен, тарифов, т.е. рост капитальных вложений в перспективе требует оценки эффективности их в соответствующем периоде. 5. Методы решения логистических задач Научную базу логистики составляет широкий спектр методов, разработанных в рамках различных дисциплин. Перечислим некоторые из них. ...

0 комментариев