Метод перебора Робертса и Флореса

2.2 Метод перебора Робертса и Флореса

В противоположность алгебраическим методам, с помощью которых пытаются найти сразу все гамильтоновы циклы и при реализации которых приходится хранить, поэтому все цепи, которые могут оказаться частями таких циклов, метод перебора имеет дело с одной цепью, непрерывно продлеваемой вплоть до момента, когда либо получается гамильтонов цикл, либо становится ясно, что эта цепь не может привести к гамильтонову циклу. Тогда цепь модифицируется некоторым систематическим способом (который гарантирует, что, в конце концов, будут исчерпаны все возможности), после чего продолжается поиск гамильтонова цикла. В этом способе для поиска требуется очень небольшой объем памяти и за один раз находится один гамильтонов цикл.

Следующая схема перебора, использующая обычную технику возвращения, была первоначально предложена Робертсом и Флоресом. Начинают с построения (k × n)-матрицы M=[mij], где элемент mij есть i-я вершина (скажем xq), для которой в графе G(X, Г) существует дуга (xj, xq). Вершины xq во множестве Г(xj) можно упорядочить произвольно, образовав элементы j-го столбца матрицы M. Число строк k матрицы M будет равно наибольшей полустепени исхода вершины.

Метод состоит в следующем. Некоторая начальная вершина (скажем, x1) выбирается в качестве отправной и образует первый элемент множества S, которое каждый раз будет хранить уже найденные вершины строящейся цепи. К S добавляется первая вершина (например, вершина a) в столбце x1. Затем к множеству S добавляется первая возможная вершина (например, вершина b) в столбце a, потом добавляется к S первая возможная вершина (например, вершина c) в столбце b и т.д. Под «возможной» вершиной мы понимаем вершину, еще не принадлежащую S. Существуют две причины, препятствующие включению некоторой вершины на шаге r во множество S = {x1, a, b, c, … , xr-1, xr}:

1)  В столбце xr нет возможной вершины.

2)  Цепь, определяемая последовательностью вершин в S, имеет длину n - 1, т.е. является гамильтоновой цепью.

В случае 2) возможны следующие случаи:

a)  В графе G существует дуга (xr, x1), и поэтому найден гамильтонов цикл.

b)  Дуга (xr, x1) не существует и не может быть получен никакой гамильтонов цикл.

В случаях (1) и (2b) следует прибегнуть к возвращению, в то время как в случае (2a) можно прекратить поиск и напечатать результат (если требуется найти только один гамильтонов цикл), или (если нужны все такие циклы) произвести печать и прибегнуть к возвращению.

Возвращение состоит в удалении последней включенной вершины xr из S, после чего остается множество S = {x1, a, b, c, … , xr-1}, и добавлении к S первой возможной вершины, следующей за xr, в столбце xr-1 матрицы M. Если не существует никакой возможной вершины, делается следующий шаг возвращения и т.д.

Поиск заканчивается в том случае, когда множество S состоит только из вершины x1 и не существует никакой возможной вершины, которую можно добавить к S, так что шаг возвращения делает множество S пустым. Гамильтоновы циклы, найденные к этому моменту, являются тогда всеми гамильтоновыми циклами, существующими в графе.

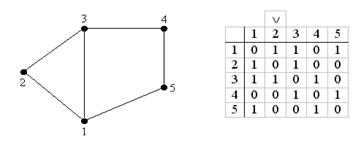
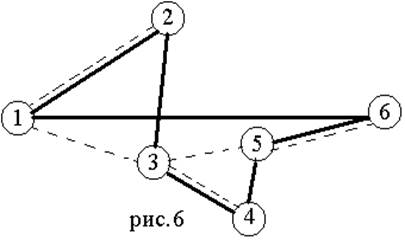
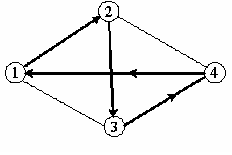
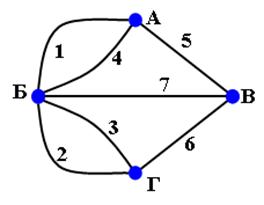
Рассмотрим пример поиска гамильтонова цикла в графе переборным методом Робертса и Флореса.

Пример:

 

"2"

1) S = {1}

2) S = {1, 2}

3) S = {1, 2, 3}

4) S = {1, 2, 3, 4}

5) S = {1, 2, 3, 4, 5} - Г 4→3 4→5

6) S = {1, 2, 3, 4}

7) S = {1, 2, 3} 3→1 3→2 3→4

8) S = {1, 2}

9) S = {1}

"3"

10) S = {1, 3} 3→2

11) S = {1, 3, 2} 2→1

12) S = {1, 3} 2→3

13) S = {1, 3, 4} 3→4 4→5

14) S = {1, 3, 4, 5, 4} 5→нет

15) S = {1, 3, 4}

16) S = {1, 3}

17) S = {1}

"5"

18) S = {1, 5}

19) S = {1, 5, 4}

20) S = {1, 5, 4, 3}

21) S = {1, 5, 4, 3, 2} - Г

22) S = {1, 5, 4, 3}

23) S = {1, 5, 4}

24) S = {1, 5}

25) S = {1}

26) S = Ø

  2.2.1 Улучшение метода Робертса и Флореса

Рассмотрим улучшение основного переборного метода Робертса и Флореса. Допустим, что на некотором этапе поиска построенная цепь задается множеством S = {x1, x2, … , xr} и что следующей вершиной, которую предполагается добавить к S, является x*S. Рассмотрим теперь две следующие ситуации, в которых вершина является изолированной в подграфе, остающемся после удаления из G(X,Г) всех вершин, образующих построенную до этого цепь.

a)  Если существует такая вершина xX\S, что xГ(xr) и Г-1(x)  S, то, добавляя к S любую вершину x*, отличную от x, мы не сможем в последующем достигнуть вершины x ни из какой конечной вершины построенной цепи, и, значит, эта цепь не сможет привести нас к построению гамильтонова цикла. Таким образом, в этом случае x является единственной вершиной, которую можно добавить к S для продолжения цепи.

b)  Если существует такая вершина xX\S, что xГ-1(x1) и Г(x) S{x*} для некоторой другой вершины x*, то x* не может быть добавлена к S, так как тогда в остающемся подграфе не может существовать никакой цепи между x и x1. Цепь, определяемая множеством S  {x*}, не может поэтому привести к гамильтонову циклу, а в качестве кандидата на добавление к множеству S следует рассмотреть другую вершину, отличную от x*.

Проверка условий (a) и (b) будет, конечно, замедлять итеративную процедуру, и для небольших графов (менее чем с 20 вершинами) не получается никакого улучшения первоначального алгоритма Робертса и Флореса. Но для больших графов эта проверка приводит к заметному сокращению необходимого времени вычислений, уменьшая его обычно в 2 или более раз.

Заключение

В данной работе мы познакомились с основными понятиями, определениями и результатами, связанными с гамильтоновыми графами и циклами. Так же мы рассмотрели ту часть теории сложности, которая затрагивает задачи отыскания гамильтонова цикла. И в итоги проведённых изучений была написана программа отыскания гамильтонова цикла в графе.

 

Список литературы

1.  Кристофидес Н. Теория графов. Алгоритмический подход. -М.: Мир, 1978.-432с.

2.  Белов В.В. Теория графов: Учеб. пособие для студ.высш.техн.учеб. заведений.-М.: Высш.школа, 1976.-392с.

3.  Культин Н.Б. Программирование в Turbo Pascal 7.0 и Delphi.- Санкт-Петербург:BHV, 1998.-240c.

4.  В.М. Бондарев, В.И. Рублинецкий, Е.Г. Качко. Основы программирования, 1998 г.

5.  Ф.А. Новиков. Дискретная математика для программистов, Питер, 2001 г.

6.  В.А. Носов. Комбинаторика и теория графов, МГТУ, 1999 г.

7.  О. Оре. Теория графов, Наука, 1982 г.

8.  www.codenet.ru

9.  www.algolist.ru

Приложение

 

Программа отыскания гамильтонова цикла в графе:

Uses

dos,crt;

VAR a,b:array[1..100,1..100] of integer;

i,j,n,ij:integer;

stro:text;

procedure ini_b; //модифицирование матрицы смежности (из А создаем В)

var i,j:integer;

begin;

for i:=1 to n do

for j:=1 to n do

b[i,j]:=a[i,j]*j;

end;

procedure ini_p1; // Формирование матрицы  из А

var i,j:integer;

s_i,s_j:string[3];

f1:text;

begin;

for i:=1 to n do

for j:=1 to n do

begin;

str(i,s_i); if i<10 then s_i:='00'+s_i else if i<100 then s_i:='0'+s_i;

str(j,s_j); if j<10 then s_j:='00'+s_j else if j<100 then s_j:='0'+s_j;

assign(f1,'vrm\p'+s_i+s_j+'.txt');

rewrite(f1);

if a[i,j]<>0 then writeln(f1,a[i,j]:4);

close(f1);

end;

end;

procedure multi_B_P1(nom:integer); //перемножение матриц  и В,

запись результата в

var ii,i,j,k,s,ip:integer;

s_i,s_j,s_k:string[3];

f1,f2:text;

label q1;

begin;

for i:=1 to n do

for j:=1 to n do

begin;

str(i,s_i); if i<10 then s_i:='00'+s_i else if i<100 then s_i:='0'+s_i;

str(j,s_j); if j<10 then s_j:='00'+s_j else if j<100 then s_j:='0'+s_j;

assign(f2,'vrm\p2'+s_i+s_j+'.txt');

rewrite(f2);

if i<>j then begin;

for k:=1 to n do

begin;

str(k,s_k); if k<10 then s_k:='00'+s_k else if k<100 then s_k:='0'+s_k;

if (b[i,k]=i) or (b[i,k]=j) or (b[i,k]=0) then goto q1;

assign(f1,'vrm\p'+s_k+s_j+'.txt');

reset(f1);

ii:=0;

ip:=0;

while not eof(f1) do begin;

ip:=0;ii:=0;

while not eoln(f1) do begin;

ip:=0;

read(f1,ip);

if (nom=1) and (ip<>0) then begin; {write(f2,ip:4);}ii:=2;end;

if (nom>1) and (ip<>0)then begin;

if ii=0 then begin;write(f2,b[i,k]:4);ii:=1;end; write(f2,ip:4);end;

end;

if ii=2 then begin;write(f2,b[i,k]:4);end;

if ii>0 then writeln(f2);

ii:=0;

readln(f1);

end;

close(f1);

q1: end;

end;

close(f2);

end;

end;

procedure rename_P1_P2; // теперь нам  уже не требуется и ей присваиваются //значения , в свою очередь в будут записаны новые данные при втором проходе

var i,j,IP1,IP2:integer;

s_i,s_j:string[3];

f1,F2:text;

AA:ARRAY[1..100] OF INTEGER;

ia,k,li,llj:integer;

label mm,mm2;

begin;

for i:=1 to n do

for j:=1 to n do

begin;

str(i,s_i); if i<10 then s_i:='00'+s_i else if i<100 then s_i:='0'+s_i;

str(j,s_j); if j<10 then s_j:='00'+s_j else if j<100 then s_j:='0'+s_j;

assign(f1,'vrm\p'+s_i+s_j+'.txt');

erase(f1);

assign(f1,'vrm\p2'+s_i+s_j+'.txt');

reset(f1);

assign(f2,'vrm\p'+s_i+s_j+'.txt');

rewrite(f2);

ia:=1; llj:=0;

while not eof(f1) do begin;

ia:=1;

while not eoln(f1) do begin;

read(f1,aa[ia]); inc(ia);

end;

if ia=1 then goto mm;

dec(ia);

for k:=1 to ia do if (aa[k]=0) or (aa[k]=i) or (aa[k]=j) then goto mm;

for k:=1 to ia do begin;

for li:=1 to k-1 do if (aa[k]=aa[li]) then goto mm2;

write(f2,aa[k]:4);llj:=1; mm2:end;

mm: readln(f1);if llj>0 then writeln(f2);

end;

close(f1);close(f2);

erase(f1);

end;

end;

procedure viv_P; // процедура использовалась при отладке программы,

отвечала за вывод на экран промежуточных матриц и

var ii,jj,i,j,k,s,ip:integer;

s_i,s_j:string[3];

f1:text;

begin;

clrscr;

for i:=1 to n do

for j:=1 to n do

begin;

str(i,s_i); if i<10 then s_i:='00'+s_i else if i<100 then s_i:='0'+s_i;

str(j,s_j); if j<10 then s_j:='00'+s_j else if j<100 then s_j:='0'+s_j;

write('p[',i,',',j,']=');

assign(f1,'vrm\p'+s_i+s_j+'.txt');

reset(f1);

ii:=0;jj:=0;

while not eof(f1) do begin;

while not eoln(f1) do begin;

read(f1,ip);

if (ii=0) and (jj>0) then write('+');

if ii>0 then write('*'); write(ip);ii:=1;

end;

readln(f1); jj:=1; II:=0;

end;

readln;

close(f1);

end;

end;

procedure viv_P2; // запись в файл example.txt промежуточных матриц

var ii,jj,i,j,k,s,ip:integer;

s_i,s_j:string[3];

f1:text;

begin;

writeln(stro,'*********************************************');

for i:=1 to n do

for j:=1 to n do

begin;

str(i,s_i); if i<10 then s_i:='00'+s_i else if i<100 then s_i:='0'+s_i;

str(j,s_j); if j<10 then s_j:='00'+s_j else if j<100 then s_j:='0'+s_j;

write(stro,'p[',i,',',j,']=');

assign(f1,'vrm\p'+s_i+s_j+'.txt');

reset(f1);

ii:=0;jj:=0;

while not eof(f1) do begin;

while not eoln(f1) do begin;

read(f1,ip);

if (ii=0) and (jj>0) then write(stro,'+');

if ii>0 then write(stro,'*'); write(stro,ip);ii:=1;

end;

readln(f1); jj:=1; II:=0;

end; writeln(stro);

close(f1);

end;

end;

procedure viv_res; // изначально использовалась для вывода результатов на экран

var ii,jj,i,j,k,s,ip,iij:integer;

ss_i,ss_j, s_i,s_j:string[3];

f1:text;

begin;

clrscr;

for i:=1 to n do

for j:=1 to n do

begin;

str(i,s_i); if i<10 then s_i:='00'+s_i else if i<100 then s_i:='0'+s_i;

str(j,s_j); if j<10 then s_j:='00'+s_j else if j<100 then s_j:='0'+s_j;

str(j,ss_j);

str(i,ss_i);

assign(f1,'vrm\p'+s_i+s_j+'.txt');

reset(f1);

ii:=0;jj:=0;iij:=0;

while not eof(f1) do begin;

while not eoln(f1) do begin;

read(f1,ip);

if (ii=0) and (jj>0) then begin;write(' '); iij:=0;end;

if ii>0 then write('-');

if iij=0 then begin;

write('CHAIN p[',i,',',j,']=',ss_j,'-',ss_i,'-');

iij:=1;

end;

write(ip);ii:=1;

end;

readln(f1); jj:=1; II:=0;

end;

if iij>0 then readln;

close(f1);

end;

end;

procedure delete_povtor; // удаление повторов и вывод результатов

var ii,jj,i,j,k,s,ip,iij:integer;

s_i,s_j:string[3];

f1:text;

et1:array[1..100,0..100] of integer;

kol_et,i3:integer;

function prov_povtor:boolean; // непосредственно проверка на повторы

var iaa,k2,l,l2:integer;

label ddd,ddd2;

begin;

for k2:=1 to et1[i,0]-1 do

if et1[i,k2]<>et1[j,k2] then goto ddd;

prov_povtor:=true;exit;

ddd:

for l:=1 to et1[i,0]-1 do

begin;

iaa:=et1[i,1];

for l2:=2 to et1[i,0]-1 do et1[i,l2-1]:=et1[i,l2];

et1[i,et1[i,0]-1]:=iaa;

for k2:=1 to et1[i,0]-1 do

if et1[i,k2]<>et1[j,k2] then goto ddd2;

prov_povtor:=true;exit;

ddd2:

end;

prov_povtor:=false;exit;

end;

label yyy;

begin;

kol_et:=1; s:=0;

for i:=1 to 100 do et1[i,0]:=1;

for i:=1 to n do

for j:=1 to n do

begin;

str(i,s_i); if i<10 then s_i:='00'+s_i else if i<100 then s_i:='0'+s_i;

str(j,s_j); if j<10 then s_j:='00'+s_j else if j<100 then s_j:='0'+s_j;

assign(f1,'vrm\p'+s_i+s_j+'.txt');

reset(f1);

while not eof(f1) do begin;

ii:=0;

while not eoln(f1) do begin;

read(f1,ip);

if ip>0 then begin;

if ii=0 then begin;

et1[kol_et,et1[kol_et,0]]:=j;

inc(et1[kol_et,0]);

et1[kol_et,et1[kol_et,0]]:=i;

inc(et1[kol_et,0]);

ii:=1;end;

et1[kol_et,et1[kol_et,0]]:=ip;

inc(et1[kol_et,0]);

end;

end;

readln(f1); ii:=0;

if (a[et1[kol_et,et1[kol_et,0]-1],et1[kol_et,1]]=1) and

(a[et1[kol_et,1],et1[kol_et,2]]=1) then inc(kol_et);

end;

close(f1);

end;

for i:=1 to kol_et-1 do begin;

for j:=1 to i-1 do begin;

if prov_povtor then goto yyy;

end;

if s=0 then begin

writeln;

writeln('Найденные пути:');end;

writeln;

s:=1; // вывод найденных путей

for k:=1 to et1[i,0]-1 do write(et1[i,k],'-'); write(et1[i,1]);

yyy: end;

if s=0 then writeln('Нет решения');

{ for i:=1 to kol_et-1 do begin;

writeln;

for j:=1 to et1[i,0]-1 do write(et1[i,j],'-');

end;}

end;

procedure delete_vrm; // удаление временных файлов

var i,j:integer;

s_i,s_j:string[3];

f1:text;

begin;

for i:=1 to n do

for j:=1 to n do

begin;

str(i,s_i); if i<10 then s_i:='00'+s_i else if i<100 then s_i:='0'+s_i;

str(j,s_j); if j<10 then s_j:='00'+s_j else if j<100 then s_j:='0'+s_j;

assign(f1,'vrm\p'+s_i+s_j+'.txt');

erase(f1);

end;

end;

BEGIN;

clrscr;

gotoxy(1,1);writeln('Программа поиска гамильтоновых циклов ');

gotoxy(1,2);writeln('Введите количество вершин графа ');

gotoxy(1,3);readln(n);

if (n<3) or (n>100) then begin;writeln('Превышены возможности программы’);

readkey;exit;end;

gotoxy(1,4);writeln('Введите матрицу смежности графа');

for i:=1 to n do begin

for j:=1 to n do begin

gotoxy(3*j,3+2*i+1);read(A[i,j]); // считывание матрицы А

if not ((A[i,j]=0) or (A[i,j]=1)) then begin

writeln(' Превышены возможности программы’');readkey;exit;end;

end;end;

ini_B;

ini_p1;

assign(stro,'vrm\example.txt');

rewrite(stro);

for ij:=1 to n-2 do begin;

multi_b_p1(ij);

rename_p1_p2;

viv_p2;

end;

close(stro);

// viv_p;

delete_povtor;

delete_vrm;

//viv_res;

readkey;

end.