Генетический алгоритм

Министерство образования и науки Республики Казахстан

Карагандинский Государственный Технический Университет

Кафедра САПР

Пояснительная записка

к курсовой работе

по дисциплине: "Прикладная теория систем"

Тема: "Генетический алгоритм"

2009

Цель работы

Выработать способность системного рассмотрения проблем и задач и дать методологию и методы их решения (вне зависимости от их проблемной ориентации). Получить практические навыки разработки базовых понятий аксиоматики, методологии исследования проектирования сложных систем. Разработка концептуальных формализованных средств, представление объектов и процессов как сложную систему. Построение обобщённых моделей, объектов и процессов как систему логико-математического аппарата их анализа и синтеза. Разработка иерархического строения систем, их целенаправленного поведения, управления и оптимизации. Научиться формализовано представлять задачу в терминах характеристик её решения, формировать наиболее адекватный критерий эффективности оценки решения, применять для этого генетический алгоритм.

Задача:

Разработать программу реализации генетического алгоритма в соответствии с выданным вариантом. Для разработки использовать любую визуальную среду программирования.

В интерфейсе программы предусмотреть возможность ввода параметров:

объём популяции;

число поколений;

коэффициент скрещивания;

коэффициент мутации;

для дифференциального кроссовера коэффициенты k,c;

для задачи коммивояжёра ввод [4. .40] числа городов и их расстановку вручную и автоматически;

для биологической задачи возможность ввода названий характеристик [10.15], их значений [4. .40], значимости и веса [0.1] каждой характеристики.

Результаты работы программы должны включать:

на каждом шаге отображать номер поколения и лучшее значение фитнес-функции в этом поколении;

лучшее значение фитнес-функции за все поколения и соответствующую ей структуру особи;

для биологической задачи и задачи оптимизации функции график зависимости значения целевой функции от номера поколения;

для задачи коммивояжёра на каждом поколении графически отображать лучщий маршрут.

Интерфейс программы должен включать характеристики генетического алгоритма в соответствии с вариантом, сведения о разработчике, краткую справку (руководство пользователя).

Вариант задания:

Тип задачи - коммивояжёр

Выбор пары - панмиксия

Кроссовер - двухточечный

Мутация - перестановка

Отбор - элитный

Критерий останова - количество поколений

Выходные данные – карта.

Анализ результатов моделирования на основе разработанной программы представляется в виде таблицы:

№ эксперимента	Кол-во маршрутов	Число поколений	Коэф. скрещивания	Коэф. мутации	Фитнес- функция (min)
1	100	500	0,5	0,001	3110
2	150	500	0,5	0,001	2783
3	200	500	0,5	0,001	2697
4	200	1000	0,5	0,001	3034
5	200	1500	0,5	0,001	2817
6	200	2000	0,5	0,001	3088
7	200	500	1	0,001	3282
8	200	500	1,5	0,001	3296
9	100	500	1	0,001	3334
10	100	500	0,5	0,01	3025
11	200	500	0,5	0,01	2511
12	100	500	1	0,01	2852
13	200	500	1	0,01	2749
14	100	500	0,5	0,1	3221
15	200	500	1	0,1	2497

Вывод:

Анализируя полученные результаты моделирования приходим к выводу, что оптимальным количеством маршрутов можно считать 200, число поколений, нет необходимости повторять алгоритм больше 500 раз (поколений), чтобы получить хороший результат. Также на значение фитнес-функции влияет коэффициент скрещивания: оптимальный коэффициент скрещивания - 1, коэффициент мутации также играет большую роль в моделировании генетического алгоритма, оптимальный коэффициент мутации - 0,1. Как видно из таблицы самое лучшее значение фитнес-функции, а значит самое минимальное расстояние за которое можно объехать 20 городов, получают за счет параметров, которые указаны в таблице в строке под номером 15.

Руководство пользователя.

Для того, чтобы открыть программу необходимо мышью дважды кликнуть по файлу “Коммивояжёр. exe”. Также необходимо проверить наличие графического документа под названием “map. bmp" в исходной папке (месте).

На экране монитора появится главное окно программы, как показано на Рис. 1

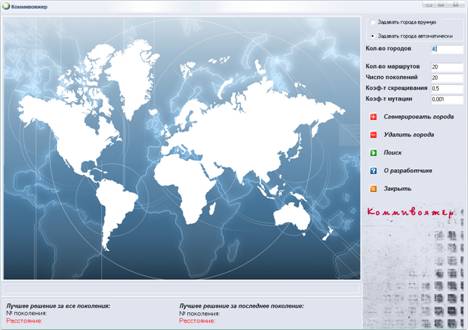
Рис. №1 Главное окно программы

В данной программе города можно задавать как вручную, для этого необходимо на карте кликнуть мышью в нужном месте, так и автоматически. Чтобы задать города автоматически необходимо в правом верхнем углу окна программы выбрать "Задать города автоматически" как показано на рис. №2.

Рис. №2

Затем ниже необходимо ввести количество городов и нажать на кнопку "Сгенерировать города". При необходимости можно очистить поле ввода городов, т.е. удалить имеющиеся города на карте нажав кнопку "Удалить города".

После того, как на карте будут отмечены необходимое количество городов (4-40), для того, чтобы застить алгоритм поиска минимального пути необходимо нажать кнопку "Поиск". Процент выполнения моделирования представлен ProgressBar-ом, который находится под картой рис. № 3.

Рис № 3. ProgressBar

По окончанию моделирования, а это произойдет тогда, когда ProgressBar полностью заполнится синим цветом, результат отобразится под ProgressBar-ом рис. № 4.

Рис. №4 Результат моделирования

Также на карте будет прорисован самый оптимальный маршрут рис. № 5.

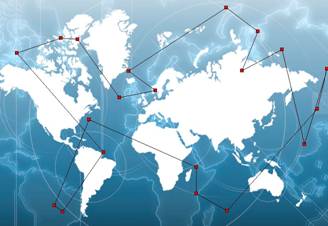
Рис. №5 Оптимальный маршрут

Также в программе предусмотрено изменение основных параметров, которые влияют на результат моделирования рис. № 6.

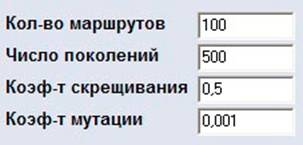
Рис. № 6. Изменяемые параметры

Листинг программы

unit Unit1;

interface

uses

Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,

Dialogs, StdCtrls, ExtCtrls;

type

TForm1 = class (TForm)

Image1: TImage;

Button1: TButton;

Edit1: TEdit;

Label1: TLabel;

Edit2: TEdit;

Label2: TLabel;

Edit3: TEdit;

Label3: TLabel;

Edit4: TEdit;

Label4: TLabel;

Edit5: TEdit;

Label5: TLabel;

procedure Image1MouseDown (Sender: TObject; Button: TMouseButton;

Shift: TShiftState; X, Y: Integer);

procedure Image1Click (Sender: TObject);

procedure FirstGeneration (Sender: TObject);

procedure CreaChildren (Sender: TObject);

procedure Mutation (Sender: TObject);

procedure TrackRead (Sender: TObject);

procedure DrawMarsh (Sender: TObject);

function CrossOver (p,m: integer): string;

procedure Mixer (Sender: TObject);

procedure Button1Click (Sender: TObject);

private

{ Private declarations }

public

{ Public declarations }

end;

var

Form1: TForm1;

pX,pY,elite: array of integer; // координаты городов, элитные

road: array of integer;

parents: array of string; // поколений родителей, детей; результат

child: array of string;

result: array of string;

gl: integer; // количество элитных

nCity,nMarsh: integer; // количество городов, маршрутов

kMut,kCross: real; // коэффициент мутации, скрещивания

implementation

{$R *. dfm}

procedure TForm1. Mixer (Sender: TObject);

var

i,j,n,k: integer;

s: string;

label lbl4;

BEGIN

n: =round ( (nMarsh) *kCross) - 1;

for i: =0 to nMarsh-1 do

begin

setLength (child,n+i+2);

child [n+i+1]: =parents [i] ;

end;

TrackRead (sender);

setlength (elite,1);

s: ='_';

{1}for i: =0 to nMarsh-1 do

begin

lbl4:

elite [0]: =random (n+nMarsh);

if pos ('_'+inttostr (elite [0]) +'_',s) <>0 then goto lbl4;

for j: =0 to n+nMarsh-1 do

begin

if pos ('_'+inttostr (j) +'_',s) =0 then

begin

if road [elite [0]] >road [j] then

begin

elite [0]: =j;

end;

end;

end;

s: =s+inttostr (elite [0]) +'_';

parents [i]: =child [elite [0]] ;

{1}end;

END;

function TForm1. CrossOver (p,m: integer): string;

var

gen: char;

i,j: integer; // счетчика

t1,t2: integer; // точки кроссовера

nC,kC: integer; // границы цикла

papa,mama: string;

label lbl3;

BEGIN

papa: =parents [p] ;

mama: =parents [m] ;

randomize;

t1: =random (nCity-1) +1; // выбираем 1 точку

lbl3:

t2: =random (nCity-1) +1; // выбираем 2 точку

if t2=t1 then goto lbl3; // 1 точка не 2 точка

if t1<t2 then // выбираем границы цикла

begin

nC: =t1;

kC: =t2;

end

else

begin

nC: =t2;

kC: =t1;

end;

for i: =nC to kC do // цикл скрещивания

begin

if pos (mama [i],papa) =0 then // проверка на совпадение генов

begin

delete (papa, i,1);

insert (mama [i],papa, i); // добавляем материнские гены

end

else

begin // изменяем повторившийся ген

gen: =papa [i] ;

papa [i]: =papa [i+1] ;

papa [i+1]: =gen;

end;

end;

crossover: =papa; // возварщаем значение функции потомка

END;

procedure TForm1. TrackRead (Sender: TObject);

var

i,j: integer;

p1,p2: integer;

p: string;

BEGIN

{1}for i: =0 to length (child) - 1 do // большой цикл по маршрутам

begin

setlength (road, i+1);

p: ='';

p: =child [i] ;

{2}for j: =1 to nCity-1 do // внутренний цикл по городам маршрутов

begin

if j<>nCity-1 then // проверка на последний город

begin

p1: =StrToInt (p [j]); //

p2: =StrToInt (p [j+1]); // соседний

end

else

begin

p1: =StrToInt (p [j+1]); // последний

p2: =StrToInt (p [1]); // первый

end; // расчет расстояния

road [i]: =road [i] +round (sqrt (sqr (pX [p1] -pX [p2]) +sqr (pY [p1] -pY [p2])));

{2}end;

{1}end;

END;

procedure TForm1. DrawMarsh (Sender: TObject);

var

i,j: integer;

p1,p2: integer;

p: string;

BEGIN

p: =parents [0] ;

Image1. CleanupInstance;

with Image1. Canvas do

begin

for j: =1 to nCity do // внутренний цикл городам маршрута

begin

if j=nCity then

begin

p1: =StrToInt (p [j]);

p2: =StrToInt (p [1]);

end

else

begin

p1: =StrToInt (p [j]);

p2: =StrToInt (p [j+1]);

end;

MoveTo (pX [p1],pY [p1]);

LineTo (pX [p2],pY [p2]);

end;

end;

END;

procedure TForm1. Mutation (Sender: TObject);

var

i,ran: integer; // счетчик, случайное число

gen: char; // мутирующий ген

mutant: string;

BEGIN

mutant: ='';

for i: =0 to round ( (nMarsh) *kCross) - 1 do // цикл мутации

begin

randomize;

if kMut<random (10) /100 then // проверка на мутацию

begin

mutant: =child [i] ; // мутирующая особь

ran: =random (nCity-1);

gen: =mutant [ran] ; //

mutant [ran]: =mutant [ran+1] ; // мутируем

mutant [ran+1]: =gen; //

child [i]: =mutant;

end;

end;

END;

procedure TForm1. FirstGeneration (Sender: TObject);

var

i,j,ram: integer; // счетчики, рандомное значение

s: string; // строка маршрута

label lbl1; // метка

BEGIN

randomize;

for i: =0 to nMarsh-1 do // цикл формирования первого поколения

{1}begin

s: ='';

setlength (parents, i+1); // устанавливаем длину массива родителей

for j: =0 to nCity-1 do // цикл формирования строки маршрута

{2}begin

setlength (s,j+1); // устанавливаем длину строки маршрута

lbl1:

ram: =random (nCity); // случайный выбор номера города

if pos (IntToStr (ram),s) =0 then // проверка на повтор номера города

begin

insert (IntToStr (ram),s,1); // добавление номера города в строку маршрута

end

else goto lbl1; // переход на метку

{2}end;

parents [i]: =s; // заполняем массив родителей (первое поколение)

{1}end;

END;

procedure TForm1. CreaChildren (Sender: TObject);

var

i: integer; // счетчики

p,m: integer; // номера родителей

label lbl2;

BEGIN

randomize;

for i: =0 to round ( (nMarsh) *kCross) - 1 do // цикл создания пар

begin

setlength (child, i+1);

p: = random (nMarsh); // выбираем номер папы

lbl2:

m: = random (nMarsh); // выбираем номер мамы

if m=p then goto lbl2; // папа не мама

child [i]: =crossover (p,m); // создаем потомков

end;

END;

procedure TForm1. Image1Click (Sender: TObject);

begin

inc (nCity); // считаем города

end;

procedure TForm1. Image1MouseDown (Sender: TObject; Button: TMouseButton;

Shift: TShiftState; X, Y: Integer);

begin

 // // /

with Image1. Canvas do

begin

Brush. Color: =clRed;

Brush. Style: =bsSolid;

Rectangle (x-5,y-5,x+5,y+5);

Brush. Color: =clWhite;

TextOut (x,y, inttostr (nCity));

end;

 // // /

SetLength (pX,nCity+1);

pX [nCity]: =x;

SetLength (py,nCity+1);

pY [nCity]: =y;

 // // /

end;

procedure TForm1. Button1Click (Sender: TObject);

var

i,nPokol: integer;

begin

nMarsh: =StrToInt (Edit3. Text);

kMut: =StrToFloat (Edit2. Text);

kCross: =StrToFloat (Edit4. Text);

nPokol: =StrToInt (Edit5. Text);

FirstGeneration (sender);

for i: =1 to nPokol do

begin

CreaChildren (sender);

Mutation (sender);

Mixer (sender);

DrawMarsh (sender);

end;

end;

end.