Пределы

3. Пределы.

Для нахождения предела выражения или функции в Maple используется команда limit (параметр 1, параметр 2). Первый параметр – выражение, второй параметр — имя переменной, приравненное значению переменной в точке предела. Необязательный третий параметр – направление предела. Если направление не задано, вычисляется стандартный двусторонний предел. Если предел не существует, в качестве ответа возвращается сообщение "undefined". Если Maple не способен вычислить предел (однако он может существовать), возвращается невыполненная команда.

> limit(cos(x)/x,x=Pi/2);

> limit((-x^2+x+1)/(x+4),x=infinity);

> limit(tan(x),x=Pi/2);

В большом количестве случаев выражение, которое не имеет двустороннего предела, имеет односторонний предел:

limit(tan(x),x=Pi/2,left);

limit(tan(x),x=Pi/2,right);

limit((1+a/x)^x,x=infinity);

В команде limit ( ) может присутствовать также необязательная опция complex или real в качестве третьего параметра аргумента. Эта опция определяет, в комплексной или действительной области вычисляется предел.

Задачи для самостоятельного решения.

1. Найти производную:

1.1. ; 1.7. ;

1.2. ; 1.8. ;

1.3. ; 1.9.;

1.4. 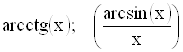; 1.10. ;

1.5. 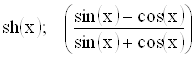; 1.11. ;

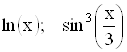1.6. ; 1.12. ;

1.13. .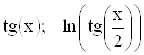

2. Найти интеграл:

2.1. 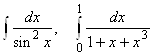, 2.7. ,

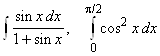2.2. 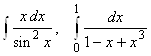, 2.8.  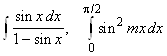при ,

2.3. 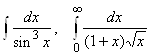, 2.9. ,

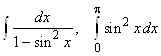2.4. 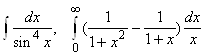, 2.10.  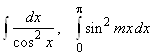при ,

2.5. 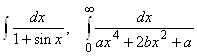, 2.11.  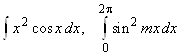при

 при ,

2.6. 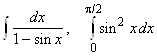, 2.12. ,

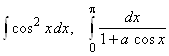2.13. .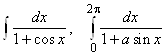

3. Найти следующие пределы:

3.1. ;

3.2. ;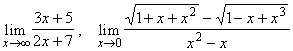

3.3. ;

3.4. ;

3.5. ;

3.6. ;

3.7. ;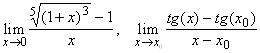

3.8. ;

3.9. ;

3.10. ;

3.11. ;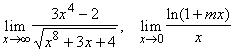

3.12. ;

3.13. .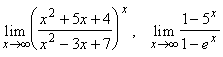

Варианты заданий.

. 1.1; 2.1; 3.1; . 1.9; 2.9; 3.9;

. 1.2; 2.2; 3.2; . 1.10; 2.10; 3.10;

. 1.3; 2.3; 3.3; . 1.11; 2.11; 3.11;

. 1.4; 2.4; 3.4; . 1.12; 2.12; 3.12;

. 1.5; 2.5; 3.5; . 1.13; 2.13; 3.13;

. 1.6; 2.6; 3.6; . 1.1; 2.2; 3.3;

. 1.7; 2.7; 3.7; . 1.13; 2.12; 3.11.

. 1.8; 2.8; 3.8;

Контрольные вопросы.

1. Команда diff ( ), ее предназначение и синтаксис.

2. Команда int ( ), ее предназначение и синтаксис.

3. Отложенные формы команд diff ( ) и int ( ).

4. Формирование производных высокого порядка с помощью оператора последовательности $.

5. Как вычислить значение определенного интеграла численным способом?

6. Назначение параметра digits в команде evalf ( ).

7. Назначение параметра flag в команде evalf ( ).

8. Команда limit( ), ее предназначение и синтаксис.

Литература

1. Говорухин В.Н., Цибулин В.Г. Введение в Maple. Математический пакет для всех. – М.: Мир, 1997. – 208 с.

2. Дьяконов В.П. Математическая система Maple V. – М.: Издательство “Солон”,1998.

3. Двайт Г.Б. Таблицы интегралов и другие математические формулы. – М.: Наука. Главная редакция физико-математической литературы, 1983. – 176 с.

4. Матросов А.В. Maple 6. Решение задач высшей математики и механики. – СПб.:БХВ - Петербург, 2001.– 528 с.

5. Манзон Б.М. Maple V Power Edition – М.: Информационно-издательский дом “Филинъ”,1998г.