Навигация
Линейный множественный регрессионный анализ
1.2. Линейный множественный регрессионный анализ
Регрессионный анализ, по-видимому, наиболее широко используемый метод многомерного статистического анализа. Термин ''множественная регрессия'' объясняется тем, что анализу подвергается зависимость одного признака (результирующего) от набора независимых (факторных) признаков. Разделение признаков на результирующий и факторные осуществляется исследователем на основе содержательных представлений об изучаемом явлении (процессе). Все признаки должны быть количественными (хотя допускается и использование дихотомических признаков, принимающих лишь два значения, например 0 и 1).При поведении экспериментов в множественной ситуации исследователь записывает показания приборов о состоянии функции отклика (y) и всех факторов, от которых она зависит (xi).
При построении регрессионных моделей, прежде всего, возникает вопрос о виде функциональной зависимости, характеризующей взаимосвязи между результирующим признаком и несколькими признаками-факторами. Выбор формы связи должен основываться на качественном, теоретическом и логическом анализе сущности изучаемых явлений. Чаще всего ограничиваются линейной регрессией, т.е. зависимостью вида [2]:
Y=a0+a1x1+a2x2+…+anxn (12)
где Y - результирующий признак; x1, …, xn - факторные признаки; a1,…,an - коэффициенты регрессии; а0 - свободный член уравнения. aiнаходим методом наименьших квадратов, для этого рассматривается функции [2]:
![]() (13)
(13)
Находим частные производные по неизвестным переменным, приравниваем к нулю и получаем систему уравнений. Решая систему, можем найти наименьшее значение функции.
Так как запись множественной регрессии (линейной) в матричной форме имеет вид [2]:
Y=X*A, (14)
где Y - это вектор-столбец опытных значений изучаемой характеристики; X –матрица всех значений всех рассматриваемых факторов, полученных при проведении измерений или наблюдений; А – вектор-столбец искомых коэффициентов аппроксимирующего полинома (12) [2]:
Y=![]() ; (15)
; (15)
X= ; (16)
; (16)
Y=![]() ;
(17)
;
(17)
Тогда функционал F метода наименьших квадратов имеет вид [2]:
![]() (18)
(18)
Для оценки адекватности рассчитанной регрессионной модели вычисляется коэффициент детерминации, он показывает, какая часть дисперсии функции отклика объясняется вариацией линейной комбинации выбранных факторов x1, x2 ,…, xj, xn [2]:
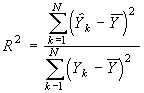 , (19)
, (19)
где ![]() - прогнозные значения
- прогнозные значения
и множественный коэффициент корреляции [2]:
![]() . (20)
. (20)
Значение коэффициента множественной корреляции оценивается с помощью таблицы 2 [1]:
Таблица Чеддока Таблица 2
| диапазон измерения | характер тесноты |
|
| слабая |
|
| умеренная |
|
| заметная |
|
| высокая |
|
| весьма высокая |
1.3. Множественный корреляционный анализ
Расчеты обычно начинают с вычисления парных коэффициентов корреляции, характеризующих тесноту связи между двумя величинами. В множественной ситуации вычисляют два типа парных коэффициентов корреляции:
1. ![]() - коэффициенты, определяющие тесноту связи между функцией отклика y и одним из факторов
- коэффициенты, определяющие тесноту связи между функцией отклика y и одним из факторов ![]() [2]:
[2]:
![]()
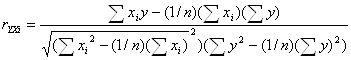 . (21)
. (21)
2. ![]() - коэффициенты, показывающие тесноту связи между одним из факторов xiи фактором xm (i, m=
- коэффициенты, показывающие тесноту связи между одним из факторов xiи фактором xm (i, m=![]() ) [2]:
) [2]:
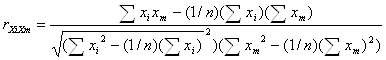 (22)
(22)
.
Значение парного коэффициента изменяется, как указывалось выше, изменяется от -1 до +1. Если, например, коэффициент ![]() - величина отрицательная, то это значит, что xiуменьшается с увеличением y. Если
- величина отрицательная, то это значит, что xiуменьшается с увеличением y. Если ![]() положителен, то xiувеличивается с увеличением y.
положителен, то xiувеличивается с увеличением y.
Значимость парных коэффициентов корреляции можно проверить двумя способами:
1) сравнение с табличным значениями ![]() [2]:
[2]:
![]() , (23)
, (23)
2) по t-критерию Стьюдента [2]:
![]() , (24)
, (24)
Где ![]() - среднеквадратическая погрешность выборочного парного коэффициента корреляции [2]:
- среднеквадратическая погрешность выборочного парного коэффициента корреляции [2]:
![]() . (25)
. (25)
Здесь ![]() определяется по таблице с числом степеней свободы
определяется по таблице с числом степеней свободы ![]() .
.
Доверительный интервал для парных коэффициентов корреляции [2]:
![]() , (26)
, (26)
где ![]() - парный коэффициент корреляции в генеральной совокупности.
- парный коэффициент корреляции в генеральной совокупности.
Если один из коэффициентов ![]() окажется равным 1, то это означает, что факторы xi и xmфункционально (не вероятностно) связаны между собой и тогда целесообразно один из них исключить из рассмотрения, причем оставляют тот фактор, у которого коэффициент
окажется равным 1, то это означает, что факторы xi и xmфункционально (не вероятностно) связаны между собой и тогда целесообразно один из них исключить из рассмотрения, причем оставляют тот фактор, у которого коэффициент ![]() больше.
больше.
После вычисления всех парных коэффициентов корреляции и исключения из рассмотрения того или иного фактора можно построить матрицу коэффициентов корреляции вида [2]:
 . (27)
. (27)
Используя матрицу (23) можно вычислить частные коэффициенты, которые показывают степень влияния одного из факторов xi на функцию отклика y при условии, что все остальные факторы закреплены на постоянном уровне. Формула для вычисления частных коэффициентов корреляции такова [2]:
![]() , (28)
, (28)
где ![]() - определитель матрицы, образованной из матрицы (27) вычеркиванием 1-й строки, i-го столбца. Определители
- определитель матрицы, образованной из матрицы (27) вычеркиванием 1-й строки, i-го столбца. Определители ![]() ,
, ![]() вычисляются аналогично. Как и парные коэффициенты, частные коэффициенты корреляции изменяются от -1 до +1.
вычисляются аналогично. Как и парные коэффициенты, частные коэффициенты корреляции изменяются от -1 до +1.
0 комментариев