Метрологические характеристики СИ
Использование СИ
В качестве норм указывают пределы допускаемых погрешностей, включающие в себя систематические и случайные составляющие
Эталоны и их использование
Вихретоковые преобразователи
Метр (м) = 100 сантиметрам (см) = 1000 миллиметрам (мм) = 1 000 000 микрометрам (мкм)
Единицы Си механических величин
Навигация
В качестве норм указывают пределы допускаемых погрешностей, включающие в себя систематические и случайные составляющие
Понятие и классификация средств измерений
54265
знаков
4
таблицы
5
изображений
1. В качестве норм указывают пределы допускаемых погрешностей, включающие в себя систематические и случайные составляющие.
Под пределом допускаемой погрешности понимается наибольшее значение погрешности средства измерений, при котором оно еще признается годным к применению. Обычно устанавливают пределы, т.е. зоны, за которую не должна выходить погрешность. Данная норма отражает то положение, что средства измерений можно применять с однократным считыванием показаний.
2. Порознь нормируют все свойства СИ, влияющие на их точность: отдельно нормируют основную погрешность, по отдельности – все дополнительные погрешности и другие свойства, влияющие на точность измерений. При выполнении данного требования обеспечивается максимальная однородность средств измерений одного типа, то есть близкие значения дополнительных погрешностей, обусловленных одними и теми же факторами. Это дает возможность заменять один прибор другим однотипным без возможного увеличения суммарной погрешности.
Пределы допускаемых погрешностей средств измерения применяются как для абсолютной, так и для относительной погрешности.
Пределы допускаемой абсолютной погрешности устанавливают по формуле ∆ = ± а для аддитивной погрешности. Для мультипликативной погрешности они устанавливаются в виде линейной зависимости
∆ = ± (а + bх),
где х – показание измерительного прибора, а и b – положительные числа, не зависящие от х.
Предел допускаемой относительной погрешности (в относительных единицах) для мультипликативной погрешности устанавливают по формуле
δ = ∆ / х = ± c.
Для аддитивной погрешности формула имеет вид:
δ = ∆ / х = ± [ c + d ( xk / x – 1)]
где xk — конечное значение диапазона измерений прибора; c и d - относительные величины.
Первое слагаемое в этой формуле имеет смысл относительной погрешности при х = хk , второе — характеризует рост относительной погрешности при уменьшении показаний прибора. Пределы допускаемой приведенной погрешности (в процентах) следует устанавливать по формуле
γ = 100∆ / xN = ± р
где xN – нормирующее значение; р - отвлеченное положительное число из ряда 1; 1,5; 2; 2,5; 4; 5; 6, умноженное на 10n ( n = 1, 0, -1, -2 и т.д.)
Нормирующее значение принимается равным: конечному значению шкалы (если 0 находится на краю шкалы), сумме конечных значений шкалы (если 0 внутри шкалы), номинальному значению измеряемой величины, длине шкалы.
1.4 Класс точности СИ и его обозначение
Установление рядов пределов допускаемых погрешностей позволяет упорядочить требования к средствам измерений по точности. Это упорядочивание осуществляется путем установления классов точности СИ.
Класс точности СИ – обобщенная характеристика данного типа СИ, отражающая уровень их точности, выражаемая пределами допускаемой основной, а в некоторых случаях и дополнительных погрешностей, а также другими характеристиками, влияющими на точность. Класс точности применяется для средств измерений, используемых в технических измерениях, когда нет необходимости или возможности выделить отдельно систематические и случайные погрешности, оценить вклад влияющих величин с помощью дополнительных погрешностей. Класс точности позволяет судить о том, в каких пределах находится погрешность средств измерений одного типа, но не является непосредственным показателем точности измерений, выполняемых с помощью каждого из этих средств. Класс точности СИ конкретного типа устанавливают в стандартах технических требований или других нормативных документах.
При выражении предела допускаемой основной погрешности в форме абсолютной погрешности класс точности в документации и на средствах измерения обозначается прописными буквами латинского алфавита или римскими цифрами. Чем дальше буква от начала алфавита, тем больше погрешность. Расшифровка соответствия букв значению абсолютной погрешности осуществляется в технической документации на средство измерения.
Выражение класса точности через относительные и приведенную погрешности рассмотрено в предыдущем разделе
В настоящее время по отношению к современным средствам измерений понятие класс точности применяется довольно редко. В основном он чаще всего используется для описания характеристик электроизмерительных приборов, аналоговых стрелочных приборов всех типов, некоторых мер длины, весов, гирь общего назначения, манометров.
Примеры обозначение классов точности для различных форм выражения погрешности приведены в таблице 1.
Таблица 1. Обозначение классов точности
| Пределы допускаемой основной погрешности | Обозначения | Форма выражения погрешности | |
| в документации | на приборе | ||
| γ = ± 1,5 | Класс точности 1,5 | 1,5 | Приведенная погрешность |
| δ = ± 0,5 | Класс точности 0,5 | 0,5 | Относительная погрешность, постоянная |
| δ = ± [ 0,02 + 0,01( xk/x –1)] | Класс точности 0,02/0,01 | 0,02/0,01 | Относительная погрешность, возрастает с уменьшением х |
Похожие работы
... повторных измерениях остаются постоянными или изменяются закономерно, обычно прогрессируя. Постоянные систематические погрешности свидетельствуют о высоких или недостаточных показателях метрологической надёжности применяемого средства измерения и могут быть устранены (учтены) предусмотренными аппаратурными методами коррекции или введением поправок в результаты измерений. Одной из распространённой ...
... причин возникновения погрешностей и уменьшение размеров погрешностей — одна из главных задач практической метрологии, поэтому понятие «погрешность» — одно из центральных в метрологии. 2. Классификация погрешностей измерений 2.1. По форме представления погрешности разделяются на абсолютные, относительные и приведённые. Абсолютная погрешность ∆ измерений, выражаемея в единицах ...
... . Так. если единицей объёма является 1 см, то объём фигуры, приведённой на рисунке 7, равен 4 см. ГЛАВА 2.Методика формирования понятия величины и её измерения у младших школьников. 2.1 Современные подходы к изучению величин в начальном курсе математики. В начальных классах рассматриваются такие величины, как: длина, площадь, масса, объём, время и ...
... Классификация малых групп Обилие малых групп в обществе предполагает их огромное разнообразие, и поэтому для целей исследований необходима их классификация. Неоднозначность понятия малой группы породила и неоднозначность предлагаемых классификаций. В принципе допустимы самые различные основания для классификации малых групп: группы различаются по времени их существования (долговременные и ...
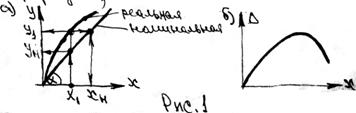
0 комментариев