Учреждение образования
“Гродненский государственный университет имени Янки Купалы”
ОБРАБОТКА ДАННЫХ
Учебная программа для специальности:
1-03 03 08-02 Олигофренопедагогика. Логопедия.
АВТОР: Шушкевич С.В., старший преподаватель кафедры математики и методики ее преподавания УО «Гродненский государственный университет имени Янки Купалы»
2009пояснительная записка
Курс содержит основы теории вероятностей и дает серьёзную подготовку по математической статистике, преимущественно по тем её разделам, которые используются при планировании и обработке экспериментов и измерений в педагогике и психологии.
Цель и задачи курса
– сообщить студентам основные теоретические сведения по общим и частным вопросам курса;
– научить студентов применять полученные знания при решении практических задач;
– учить студентов самостоятельно работать с научной литературой;
– развивать у студентов аналитическое, логическое мышление и математическую речь.
Знания, умения и навыки, приобретаемые студентами при изучении курса.
Студенты должны знать:
– основные понятия теории вероятностей и математической статистики;
– формы подготовки и представления экспериментальных данных;
– методы математической статистики, используемые при планировании, проведении и обработке результатов экспериментов в педагогике и психологии.
Студенты должны уметь:
– планировать процесс математико–статистической обработки экспериментальных данных;
– практически рассчитывать типовые для педагогики и психологии статистические задачи;
– пользоваться статистическими таблицами при проведении расчетов и формировании выводов и заключений;
– анализировать полученные результаты.
Курс рассчитан на 36 аудиторных часов.
ПРИМЕРНЫЙ ТЕМАТИЧЕСКИЙ ПЛАН КУРСА
Лекции – 16 часов, лабораторные занятия – 20 часов.
| № п/п | Тема | Количество часов | |
| лекции | практические занятия | ||
| 1. | Введение в теорию вероятностей. | 2 | |
| 2. | Методы математической статистики. | 6 | 8 |
| 3. | Непараметрические методы анализа данных. | 8 | 12 |
| Всего | 16 | 20 | |
СОДЕРЖАНИЕ
Основные понятия теории вероятностей
Примеры стохастических явлений: рост людей, разброс показателей способностей, скорость реакции. Частота случайного события. Устойчивость частот. Примеры.
Классическое определение вероятности.
Случайная величина. Непрерывные и дискретные случайные величины. Числовые характеристики случайной величины. Функция распределения, плотность распределения случайной величины, их свойства.
Виды функций распределения. Биномиальное распределение. Распределение Пуассона. Т-распределение Стьюдента. Распределение c2.
Нормальное распределение. Качественное и количественное сопоставление эмпирического распределения теоретическому.
Математическое ожидание случайной величины, его свойства. Дисперсия, её свойства, среднеквадратичное отклонение случайной величины. Примеры.
Корреляционный момент. Коэффициент корреляции, его свойства.
Ковариация.
Требования к компетентности:
знать основные понятия теории вероятностей;
понимать содержание основных понятий теории вероятностей;
уметь использовать научную терминологию при решении классических задач теории вероятностей.
Основы математической статистики
Определение прикладной статистики. Основные этапы статистической обработки данных. Принципы группировки информации. Статистические таблицы. Графические методы представления информации.
Генеральная совокупность. Случайная выборка.
Вариационный ряд. Объём вариационного ряда. Размах. Частота. Накопленная частота. Дискретный ряд. Интервальный вариационный ряд, способы его построения. Графическое представление вариационных рядов: полигон, гистограмма, кумулянта, огива.
Выборочные характеристики – среднее, дисперсия, среднеквадратичное отклонение и способы их вычисления.
Асимметрия, эксцесс, их интерпретация, связь с видом распределения.
Мода, способы её вычисления в дискретных и интервальных вариационных рядах. Понятие бимодальности, полимодальности ряда.
Медиана, способы её вычисления в дискретных и интервальных вариационных рядах.
Меры центральной тенденции - мода, медиана, среднее - и их соотношение как априорная характеристика вида эмпирического распределения выборки.
Основные понятия, связанные с проверкой статистических гипотез: гипотезы H0, H1, критическое множество, ошибки первого и второго рода, уровень значимости, мощность. Число степеней свободы.
Предельная ошибка и необходимый объем выборки.
Проверка нормальности эмпирического распределения по Плохинскому, по Пустыльнику. λ критерий Колмогорова – Смирнова. Критерий Шапиро – Уилки.
Доверительный интервал. Правило 3σ.
Проверка статистических гипотез об однородности двух нормально распределенных выборок с помощью критерия Стьюдента. Критерий оценки для сравнения средних. F – критерий для сравнения дисперсий.
Меры связи. Коэффициент корреляции Пирсона, его свойства, интерпретация. Корреляционный анализ. Достоверность коэффициента корреляции.
Линейная регрессия. Метод наименьших квадратов. Коэффициент регрессии. Уравнение регрессии, способ его построения. Точечные оценки и доверительные интервалы для параметров линейной регрессии.
Нелинейная корреляционная зависимость. Корреляционное отношение η2.
Интерпретация значений коэффициента корреляции.
Дисперсионный анализ, суть метода.
Однофакторный дисперсионный анализ, алгоритм расчета. Однофакторный дисперсионный анализ с неравными объёмами выборок.
Двухфакторный дисперсионный анализ. Двухфакторный дисперсионный анализ с одинаковым числом наблюдений. Двухфакторный дисперсионный анализ с параллельными наблюдениями на сочетаниях уровней факторов.
Требования к компетентности:
знать:
– основные понятия математической статистики;
– формы подготовки и представления экспериментальных данных;
– методы математической статистики, используемые при планировании, проведении и обработке результатов экспериментов в педагогике и психологии;
уметь:
– планировать процесс математико–статистической обработки экспериментальных данных;
– практически рассчитывать типовые для педагогики и психологии статистические задачи;
– пользоваться статистическими таблицами при проведении расчетов и формировании выводов и заключений;
– анализировать полученные результаты.
Непараметрические методы статистического анализа
Типы измерений данных в психологии. Номинальные, порядковые интервальные и относительные шкалы измерений.
Ранжирование. Ранг. Связанные ранги, способы их вычисления.
Квантили: децили, квинтили, квартили, процентили, их вычисление и соотношение между собой.
Измерение связей между разнотипными данными. Коэффициент сопряженности. Коэффициент ассоциации. Коэффициенты взаимной сопряженности Пирсона и Чупрова. Коэффициент корреляции τ Кендалла. Коэффициент ранговой корреляции Спирмена. Биссериальный коэффициент корреляции. Биссериальная ранговая корреляция. Коэффициент конкордации.
Номинальные шкалы. Дихотомические переменные. Биномиальный критерий и критерий c2 для проверки соответствия выборочной статистики параметру генеральной совокупности. Построение и анализ таблиц сопряженности признаков 2´2. Критерий точной вероятности Фишера. Критерий c2. Схема “до – после”. Критерий значимости изменений Макнимара. Q – критерий Кокрена.
Порядковые шкалы измерений. Критерий Колмогорова – Смирнова. U - критерий Манна – Уитни для сравнения средних, критерий Вальда – Вольфовица для исследования гипотез о различиях в распределении. Критерий знаков. Критерий множественных сравнений Уилкоксона для оценки статистической значимости всевозможных пар воздействий. Знаково – ранговый критерий Уилкоксона для сравнения средних. Двухфакторный дисперсионный анализ по Фридману.
Критерий φ* - угловое преобразование Фишера. Q – критерий Розенбаума. Н – критерий Крускала – Уолисса.
Интервальные шкалы. Стэны. Критерий рандомизации.
Использование статистических таблиц.
Требования к компетентности:
знать:
– методы определения типов данных в педагогике и психологии, назначние методов непараметрической статистики в зависимости от типа данных, назначение статистических таблиц;
уметь:
– планировать процесс математико–статистической обработки экспериментальных данных, распределение которых отличается от нормального;
– практически рассчитывать статистические задачи, возникающие в педагогике и психологии;
– пользоваться статистическими таблицами при проведении расчетов и формировании выводов и заключений;
– анализировать полученные результаты.
ЛИТЕРАТУРА
1. Артемьева Е.Ю., Мартынов Е.М. Вероятностные методы в психологии. – М.: Изд-во Московского университета. – 1975. – 206 с.
2. Гласс Дж., Стенли Дж. Статистические методы в педагогике и психологии. – М.: Прогресс. – 1976. – 494 с.
3. Гнеденко В.В. Курс теории вероятностей. – М.: Наука. – 1973. – 400 с.
4. Ермолаев О.Ю. Математическая статистика для психологов. – М.: Флинта. – 2003. – 336с.
5. Кендалл М., Стюарт А. Статистические выводы и связи. – М.: Наука. – 1973.
6. Кокс Д., Снелл Э. Прикладная статистика: принципы и примеры. – М.: Мир. – 1984.
7. Крылов В.Ю. Геометрическое представление данных психологических исследований. – М.: Наука. – 1990.
8. Лакин Г.Ф. Биометрия. – М.: Высшая школа. – 1973. – 343 с.
9. Лбов Г.С. Методы обработки разнотипных данных. – М.: Наука. – 1981.
10. Математические методы в исследованиях индивидуальной и групповой деятельности п/ред. Крылова В.Ю. – М.: Наука. – 1990.
11. Мацкевич И.П., Свирид Г.П. Высшая математика. Теория вероятностей и математическая статистика. – Мн.: Вышэйшая школа. – 1993. – 269 с.
12. Митропольский А.К. Техника статистических вычислений. – М.: Наука. – 1971.
13. Основы математической статистики. Учебное пособие для институтов физической культуры п/ред. В.С. Иванова. – М.: Физкультура и спорт. – 1990. – 174 с.
14. Поллард Дж. Справочник по вычислительным методам статистики. – М.: Финансы и статистика. – 1982. – 343 с.
15. Ракицкий П.Ф. Биологическая статистика. – Мн.: Вышэйшая школа. – 1967. – 396 с.
16. Сидоренко Е.В. Методы математической обработки в психологии. С.-Петербург. – 1996. – 349 с.
17. Справочник по прикладной статистике п/ред. Ллойда и др. – М.: Финансы и статистика. – 1989.
18. Суходольский Г.В. Основы математической статистики для психологов. – Изд-во Ленинградского университета. – 1998. – 461 с.
19. Холлендер М., Вулф Д.А. Непараметрические методы статистики. М.: Финансы и статистика. – 1983. – 517 с.
20. Эренберг А. Анализ и интерпретация статистических данных. – М.: Финансы и статистика. – 1981. – 406 с.
Похожие работы
... распределения случайной величины. а) коэффициент асимметрии; б) момент случайной величины; в) коэффициент эксцесса; г) математическое ожидание. Ответ: в). Тема 9. МЕТОДЫ ВТОРИЧНОЙ СТАТИСТИЧЕСКОЙ ОБРАБОТКИ РЕЗУЛЬТАТОВ ПЕДАГОГИЧЕСКОГО ЭКСПЕРИМЕНТА Тестовое задание 1. Выберите верные ответы. В зависимости от используемых источников информации исследования делятся на: а) кабинетные; б) ...
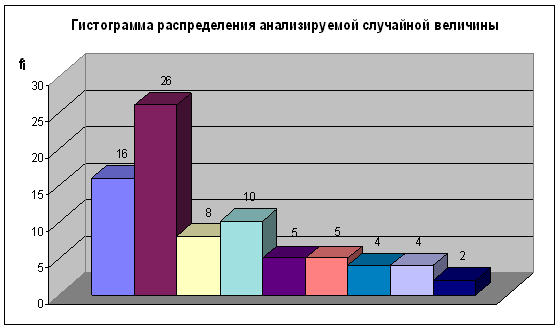
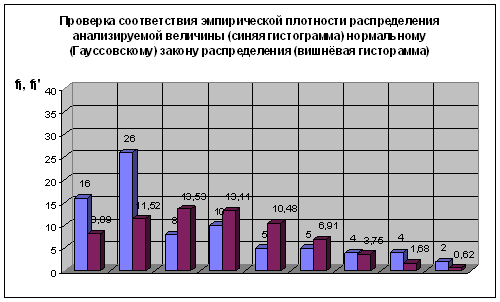
... эмпирической плотности распределения случайной анализируемой величины и расчёт её характеристик Определяем размах имеющихся данных, т.е. разности между наибольшим и наименьшим выборочным значениями (R = Xmax – Xmin): Выбор числа интервалов группировки k при числе наблюдений n<100 – ориентировочное значение интервалов можно рассчитать с использованием формулы Хайнхольда и Гаеде: ...
... ) опытных значений показателя надежности на генеральную совокупность: (1.40) 1.9 Определение минимального числа объектов наблюдения при оценке показателей надежности Точность определения показателей надежности зависит при прочих равных условиях от объема информации, т.е. от числа испытуемых объектов. Как известно, с увеличением количества испытуемых объектов N доверительные границы ...
... -регрессивного анализа я определяю между фондом заработной платы и фондоотдачей основных фондов. 7.1 Определение тесноты парной связи и формы для всей статистической совокупности 7.1.1Линейная форма зависимости Таблица 7.1 № x y Xy x2 y2 Yx 1 33,6 0,909494725 30,55902277 1128,96 0,827180655 1,046650876 2 63,2 0,803056027 50,75314092 3994,24 0, ...



0 комментариев