Навигация
Обработка статистической информации
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Государственное образовательное учреждение высшего профессионального образования
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»
КАФЕДРА ЭКОНОМИКИ И ФИНАНСОВ
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
К КУРСОВОЙ РАБОТЕ
по дисциплине: СТАТИСТИКА
РАБОТУ ВЫПОЛНИЛ
СТУДЕНТ ГР.
816к Д.С. Гончарова
Санкт-Петербург 2010
Содержание
Введение
1. Относительные показатели
1.1 Среднемесячная заработная плата работника предприятия.
1.2 Доля заработной платы работников предприятия в объеме продукции
1.3 Фондоотдача основных фондов
2. Средние показатели
3. Группировка статистических данных
3.1 Простая аналитическая группировка
3.2 Комбинационная группировка
4. Проверка статистической совокупности на однородность
5. Определение взаимосвязи между двумя показателями (с использованием дисперсий)
6. Определение тесноты взаимосвязи между показателями с помощью коэффициента ранговой корреляции
7. Определение тесноты парной связи и формы связи с использованием корреляционно- регрессивного анализа между признаками
7.1 Определение тесноты парной связи и формы для всей статистической совокупности
7.1.1Линейная форма зависимости
7.1.2 Степенная форма зависимости
7.2 Определение тесноты парной связи и формы связи для групп, полученных в результате простой группировки
8. Сравнение и анализ расчетов
9. Исследование тесноты линейной множественной связи
9.1 Парные коэффициенты корреляции
9.2 Множественный коэффициент корреляции
9.3 Частные коэффициенты корреляции
9.4 Коэффициент конкордации
Заключение
Список литературы
Введение
Цель работы: изучение и освоение различных методов обработки статистической информации.
Для достижения поставленной цели необходимо выполнить следующие задачи:
· определить относительные показатели по предприятиям;
· рассчитать средние показатели по всей совокупности предприятий;
· выполнить группировку статистической информации;
· осуществить проверку статистической совокупности на однородность с использованием коэффициента вариации;
· определить взаимосвязь (с использованием дисперсий) между показателями;
· с использованием коэффициента ранговой корреляции определить тесноту взаимосвязи между показателями;
· определить тесноту парной связи и форму связи с использованием корреляционно-регрессионного анализа между признаками;
· исследовать линейную и нелинейную зависимость;
· исследовать тесноту линейной множественной связи
· определить:
а) Коэффициент конкордации.
б) Множественный коэффициент корреляции.
в) Парные коэффициенты корреляции.
г) Частные коэффициенты корреляции.
1. Относительные показатели
1.1 Среднемесячная заработная плата работника предприятияСреднемесячная заработная плата рабочего по всей совокупности предприятий рассчитывается по формуле:
![]()
ФЗП- Фонд заработной платы (без учета выплат в различные фонды),
N- Среднесписочная численность работающих, чел.
Таблица 1.1
| № | Фонд заработной платы (без учета выплат в различные фонды), млн р | Среднесписочная числен-ность работающих, чел. | Среднемесячная заработная плата работника предприятия, тыс. р/мес. |
| 1 | 33,6 | 205 | 13,65854 |
| 2 | 63,2 | 267 | 19,72534 |
| 3 | 241,0 | 668 | 30,06487 |
| 4 | 275,3 | 714 | 32,13119 |
| 5 | 159,7 | 544 | 24,46385 |
| 6 | 209,0 | 622 | 28,00107 |
| 7 | 251,8 | 683 | 30,7223 |
| 8 | 286,3 | 728 | 32,77244 |
| 9 | 149,3 | 526 | 23,65336 |
| 10 | 93,4 | 267 | 29,15106 |
| 11 | 406,9 | 868 | 39,0649 |
| 12 | 80,6 | 228 | 29,45906 |
| 13 | 278,2 | 718 | 32,28877 |
| 14 | 70,9 | 270 | 21,88272 |
| 15 | 92,0 | 413 | 18,56336 |
| 16 | 260,8 | 695 | 31,27098 |
| 17 | 71,6 | 364 | 16,39194 |
| 18 | 191,0 | 595 | 26,7507 |
| 19 | 450,9 | 914 | 41,1105 |
| 20 | 120,5 | 320 | 31,38021 |
| 21 | 79,7 | 256 | 25,94401 |
| 22 | 175,5 | 570 | 25,65789 |
| 23 | 38,1 | 229 | 13,86463 |
| 24 | 417,4 | 879 | 39,57148 |
| 25 | 343,9 | 798 | 35,9127 |
Фондоотдача основных фондов по всей совокупности предприятий рассчитывается по формуле:
![]()
Q- Объем товарной продукции,
Ф- Среднегодовая стоимость основных фонов.
Таблица 1.2
| № | Объем товарной продукции, млн. р. | Среднегодовая стоимость основных фондов, млн. р. | Фондоотдача основных фондов |
| 1 | 163,8 | 180,1 | 0,909495 |
| 2 | 236,5 | 294,5 | 0,803056 |
| 3 | 843,3 | 420,8 | 2,00404 |
| 4 | 1005,9 | 469,7 | 2,14158 |
| 5 | 696,3 | 426,9 | 1,631061 |
| 6 | 1031,3 | 552,4 | 1,866944 |
| 7 | 1361,2 | 664,6 | 2,048149 |
| 8 | 1712,9 | 784,2 | 2,184264 |
| 9 | 538,9 | 341,8 | 1,576653 |
| 10 | 350,4 | 438 | 0,8 |
| 11 | 2149,9 | 825,4 | 2,604677 |
| 12 | 352,8 | 179,8 | 1,96218 |
| 13 | 1187,1 | 551,5 | 2,152493 |
| 14 | 262,4 | 323,4 | 0,811379 |
| 15 | 438,8 | 354,2 | 1,238848 |
| 16 | 1150,5 | 551,9 | 2,084617 |
| 17 | 249,4 | 228,3 | 1,092422 |
| 18 | 655,3 | 367,4 | 1,783615 |
| 19 | 2549,5 | 930,3 | 2,740514 |
| 20 | 536,8 | 179,6 | 2,988864 |
| 21 | 311,2 | 404,8 | 0,768775 |
| 22 | 809,7 | 473,3 | 1,710754 |
| 23 | 166,7 | 180,4 | 0,924058 |
| 24 | 2185,1 | 828,3 | 2,638054 |
| 25 | 2066,2 | 862,8 | 2,394761 |
Месячная производительность труда одного рабочего по всей совокупности предприятий рассчитывается по формуле:
![]()
Q- Объем товарной продукции,
Np- Среднесписочная численность рабочих.
Таблица 1.3
| № | Объем товарной продукции, млн. р. | Среднесписочная численность рабочих, чел. | Месячная производительность труда одного рабочего, тыс. р/чел. |
| 1 | 163,8 | 205 | 0,0000665854 |
| 2 | 236,5 | 267 | 0,0000738140 |
| 3 | 843,3 | 668 | 0,0001052021 |
| 4 | 1005,9 | 714 | 0,0001174020 |
| 5 | 696,3 | 544 | 0,0001066636 |
| 6 | 1031,3 | 622 | 0,0001381699 |
| 7 | 1361,2 | 683 | 0,0001660810 |
| 8 | 1712,9 | 728 | 0,0001960737 |
| 9 | 538,9 | 526 | 0,0000853771 |
| 10 | 350,4 | 267 | 0,0001093633 |
| 11 | 2149,9 | 868 | 0,0002064036 |
| 12 | 352,8 | 228 | 0,0001289474 |
| 13 | 1187,1 | 718 | 0,0001377786 |
| 14 | 262,4 | 270 | 0,0000809877 |
| 15 | 438,8 | 413 | 0,0000885391 |
| 16 | 1150,5 | 695 | 0,0001379496 |
| 17 | 249,4 | 364 | 0,0000570971 |
| 18 | 655,3 | 595 | 0,0000917787 |
| 19 | 2549,5 | 914 | 0,0002324489 |
| 20 | 536,8 | 320 | 0,0001397917 |
| 21 | 311,2 | 256 | 0,0001013021 |
| 22 | 809,7 | 570 | 0,0001183772 |
| 23 | 166,7 | 229 | 0,0000606623 |
| 24 | 2185,1 | 879 | 0,0002071578 |
| 25 | 2066,2 | 798 | 0,0002157686 |
2. Средние показатели
Средние показатели по всей совокупности предприятий рассчитываются по следующим формулам:
![]() ;
; 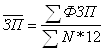 ;
; 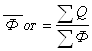 ;
;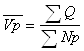 .
.
Таблица 2.1
| № | Среднеспи-сочная численность рабочих, чел. | Среднемесячная заработная плата работника, тыс. р/мес. | Фондоотдача основных фондов | Среднемесячная производительность труда одного рабочего, тыс. р/чел. |
| 1 | 205 | 13,65854 | 0,909495 | 0,0000665854 |
| 2 | 267 | 19,72534 | 0,803056 | 0,0000738140 |
| 3 | 668 | 30,06487 | 2,00404 | 0,0001052021 |
| 4 | 714 | 32,13119 | 2,14158 | 0,0001174020 |
| 5 | 544 | 24,46385 | 1,631061 | 0,0001066636 |
| 6 | 622 | 28,00107 | 1,866944 | 0,0001381699 |
| 7 | 683 | 30,7223 | 2,048149 | 0,0001660810 |
| 8 | 728 | 32,77244 | 2,184264 | 0,0001960737 |
| 9 | 526 | 23,65336 | 1,576653 | 0,0000853771 |
| 10 | 267 | 29,15106 | 0,8 | 0,0001093633 |
| 11 | 868 | 39,0649 | 2,604677 | 0,0002064036 |
| 12 | 228 | 29,45906 | 1,96218 | 0,0001289474 |
| 13 | 718 | 32,28877 | 2,152493 | 0,0001377786 |
| 14 | 270 | 21,88272 | 0,811379 | 0,0000809877 |
| 15 | 413 | 18,56336 | 1,238848 | 0,0000885391 |
| 16 | 695 | 31,27098 | 2,084617 | 0,0001379496 |
| 17 | 364 | 16,39194 | 1,092422 | 0,0000570971 |
| 18 | 595 | 26,7507 | 1,783615 | 0,0000917787 |
| 19 | 914 | 41,1105 | 2,740514 | 0,0002324489 |
| 20 | 320 | 31,38021 | 2,988864 | 0,0001397917 |
| 21 | 256 | 25,94401 | 0,768775 | 0,0001013021 |
| 22 | 570 | 25,65789 | 1,710754 | 0,0001183772 |
| 23 | 229 | 13,86463 | 0,924058 | 0,0000606623 |
| 24 | 879 | 39,57148 | 2,638054 | 0,0002071578 |
| 25 | 798 | 35,9127 | 2,394761 | 0,0002157686 |
| Среднее | 533,64 | 30,236364 | 1,947784 | 0,143742 |
3. Группировка статистических данных 3.1 Простая аналитическая группировка
Величина равных интервалов определяется по формуле:
![]()
где ![]() и
и ![]() - максимальное и минимальное значение признака;
- максимальное и минимальное значение признака;
n - заданное количество интервалов группировки
Анализ данных таблицы 3.1 показывает, что самое большое количество предприятий находится в первой группе, а наименьшее в четвертой. Фондоотдача основных фондов, среднесписочная численность рабочих и среднемесячная заработная плата работника предприятия находятся в прямой зависимости от фонда заработной платы.
3.2 Комбинационная группировкаСогласно исходным данным группировочные признаки: фонд заработной платы и фондоотдача основных фондов, а результативными являются среднесписочная численность рабочих, производительность труда одного рабочего.
∆1=104,325
∆2![]()
Таблица 3.2
| Номер групппы | Группы фирм | Номера фирм | Среднесписочная численность рабочих, чел. | Производительность труда одного рабочего, р/чел. | ||||
| По Фонду заработной платы, тыс.р. | По фондоотдаче основных фондов | Суммарная | Средняя | Суммарная | Средняя | |||
| I | 33,6-137,925 | 0,768775-1,8788195 | 1,2,10, 14,15, 17,21,23 | 2271 | 283,875 | 0,0006383509 | 0,0000797939 | |
| 1,8788195-2,988864 | 12,20 | 548 | 274 | 0,0002687390 | 0,0001343695 | |||
| Итого: | 10 | 2819 | 281,9 | 0,0009070899 | 0,00009070899 | |||
| II | 137,925-242,25 | 0,768775-1,8788195 | 5,6,9,18, 22 | 2857 | 571,4 | 0,0005403664 | 0,000108073 | |
| 1,8788195-2,988864 | 3 | 668 | 668 | 0,0001052021 | 0,0001052021 | |||
| Итого: | 6 | 3525 | 587,5 | 0,0006455685 | 0,000107595 | |||
| III | 242,25- 346,575 | 0,768775-1,8788195 | 0 | 0 | 0 | 0 | 0 | |
| 1,8788195-2,988864 | 4,7,8,13,16,25 | 4336 | 722,66666 | 0,0009710535 | 0,000161842 | |||
| Итого: | 6 | 4336 | 722,66666 | 0,0009710535 | 0,000161842 | |||
| IV | 346,575-450,9 | 0,768775-1,8788195 | 0 | 0 | 0 | 0 | 0 | |
| 1,8788195-2,988864 | 11,19,24 | 2661 | 887 | 0,0006460103 | 0,000215337 | |||
| Итого: | 3 | 2661 | 887 | 0,0006460103 | 0,000215337 | |||
Наибольшее количество предприятий состоит в первой группе, наибольшая производительность труда одного рабочего у предприятий входящих в 4 группу, а так же в этой группе наибольшие показатели среднесписочной численности рабочих. Среднесписочная численность рабочих и производительность труда одного рабочего находятся в прямой зависимости с фондом заработной платы и фондоотдачей основных фондов.
4. Проверка статистической совокупности на однородность
В своей работе проверку статистической совокупности на однородность я произвожу с использованием коэффициента вариации по признаку Фонд заработной платы.
Таблица 4.1
| ФЗП(Xi) | Xi-X | (Xi-X)^2 |
| 33,6 | -160,024 | 25607,68 |
| 63,2 | -130,424 | 17010,42 |
| 241 | 47,376 | 2244,485 |
| 275,3 | 81,676 | 6670,969 |
| 159,7 | -33,924 | 1150,838 |
| 209 | 15,376 | 236,4214 |
| 251,8 | 58,176 | 3384,447 |
| 286,3 | 92,676 | 8588,841 |
| 149,3 | -44,324 | 1964,617 |
| 93,4 | -100,224 | 10044,85 |
| 406,9 | 213,276 | 45486,65 |
| 80,6 | -113,024 | 12774,42 |
| 278,2 | 84,576 | 7153,1 |
| 70,9 | -122,724 | 15061,18 |
| 92 | -101,624 | 10327,44 |
| 260,8 | 67,176 | 4512,615 |
| 71,6 | -122,024 | 14889,86 |
| 191 | -2,624 | 6,885376 |
| 450,9 | 257,276 | 66190,94 |
| 120,5 | -73,124 | 5347,119 |
| 79,7 | -113,924 | 12978,68 |
| 175,5 | -18,124 | 328,4794 |
| 38,1 | -155,524 | 24187,71 |
| 417,4 | 223,776 | 50075,7 |
| 343,9 | 150,276 | 22582,88 |
| 4840,6 | 0 | 368807,2 |
Среднее линейное отклонение – это среднее значение отклонений вариантов признака от их средней величины:
X=193,624
 ,
, ![]()
xi – варианты признака
х – средняя величина признака
n – численность единиц совокупности
![]()
На основе вышеприведенных расчетов можно сделать вывод о том, что статистическая совокупность не однородна, так как коэффициент вариации > 25%.
Далее я рассчитываю коэффициенты вариации для простой группировки.
Для первой группы:
Таблица 4.2
| Xi | Xi-X10 | (Xi-X)^2 |
| 33,6 | -40,76 | 1661,378 |
| 63,2 | -11,16 | 124,5456 |
| 93,4 | 19,04 | 362,5216 |
| 80,6 | 6,24 | 38,9376 |
| 70,9 | -3,46 | 11,9716 |
| 92 | 17,64 | 311,1696 |
| 71,6 | -2,76 | 7,6176 |
| 120,5 | 46,14 | 2128,9 |
| 79,7 | 5,34 | 28,5156 |
| 38,1 | -36,26 | 1314,788 |
| 743,6 | 0 | 5990,344 |
X=74,36
σ=24,47518
![]()
На основе вышеприведенных расчетов можно сделать вывод о том, что статистическая совокупность не однородна, так как коэффициент вариации > 25%.
Нужно произвести перегруппировку.
Для второй группы:
Таблица 4.3
| Xi | Xi-X6 | (Xi-X)^2 |
| 241 | 53,4167 | 2853,34 |
| 159,7 | -27,8833 | 777,4803 |
| 209 | 21,4167 | 458,6736 |
| 149,3 | -38,2833 | 1465,614 |
| 191 | 3,41667 | 11,67361 |
| 175,5 | -12,0833 | 146,0069 |
| 1125,5 | 0 | 5712,788 |
X=187,5833
σ=30,85663
![]()
На основе вышеприведенных расчетов можно сделать вывод о том, что статистическая совокупность однородна, так как коэффициент вариации < 25%.
Для третьей группы:
Таблица 4.4
| Xi | Xi-X6 | (Xi-X)^2 |
| 275,3 | -7,41667 | 55,00694 |
| 251,8 | -30,9167 | 955,8403 |
| 286,3 | 3,583333 | 12,84028 |
| 278,2 | -4,51667 | 20,40028 |
| 260,8 | -21,9167 | 480,3403 |
| 343,9 | 61,18333 | 3743,4 |
| 1696,3 | 0 | 5267,828 |
X=282,7167
σ=29,63058
![]()
На основе вышеприведенных расчетов можно сделать вывод о том, что статистическая совокупность однородна, так как коэффициент вариации < 25%.
Для четвертой группы:
Таблица 4.5
| Xi | Xi-X | (Xi-X)^2 |
| 406,9 | -18,1667 | 330,0278 |
| 450,9 | 25,83333 | 667,3611 |
| 417,4 | -7,66667 | 58,77778 |
| 1275,2 | 0 | 1056,167 |
X=425,0667
σ=13,26755
![]()
На основе вышеприведенных расчетов можно сделать вывод о том, что статистическая совокупность однородна, так как коэффициент вариации < 25%.
5. Определение взаимосвязи между двумя показателями (с использованием дисперсий)
Все явления общественной жизни взаимосвязаны и взаимообусловлены. Задача состоит в том, чтобы выявить и измерить связи и зависимости между изучаемыми явлениями.
Эмпирическое корреляционное отношение – это показатель тесноты связи между взаимосвязанными явлениями.
Таблица 5.1
| № | Фонд заработной платы, млн. р. | Фондоотдача основных фондов |
| 1 | 33,6-137,925 | 0,909494725 |
| 0,803056027 | ||
| 0,8 | ||
| 1,9621802 | ||
| 0,811379097 | ||
| 1,238848108 | ||
| 1,092422251 | ||
| 2,988864143 | ||
| 0,768774704 | ||
| 0,92405765 | ||
| 2 | 137,925-242,25 | 2,004039924 |
| 1,631061138 | ||
| 1,866944243 | ||
| 1,576653013 | ||
| 1,783614589 | ||
| 1,710754278 | ||
| 3 | 242,25- 346,575 | 2,141579732 |
| 2,048149263 | ||
| 2,184264218 | ||
| 2,1524932 | ||
| 2,084616778 | ||
| 2,394761242 | ||
| 4 | 346,575-450,9 | 2,60467652 |
| 2,740513813 | ||
| 2,638053845 |
Я определяю взаимосвязь между фондом заработной платы и фондоотдачей основных фондов.
![]()
![]()
![]()
![]()
Далее я рассчитываю среднее значение фондоотдачи основных фондов:
![]()
Рассчитываю для каждой группы групповую дисперсию.
Групповая дисперсия рассчитывается по формуле:
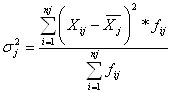
Дисперсия для 1 группы:
Таблица 5.2
|
|
|
|
| 0,909494725 | -0,320412965 | 0,102664468 |
| 0,803056027 | -0,426851663 | 0,182202343 |
| 0,8 | -0,429907691 | 0,184820622 |
| 1,9621802 | 0,73227251 | 0,536223028 |
| 0,811379097 | -0,418528593 | 0,175166184 |
| 1,238848108 | 0,008940418 | 0,0000799 |
| 1,092422251 | -0,137485439 | 0,018902246 |
| 2,988864143 | 1,758956452 | 3,0939278 |
| 0,768774704 | -0,461132987 | 0,212643632 |
| 0,92405765 | -0,305850041 | 0,093544247 |
| Итого: | - | 4,600174502 |
![]()
Дисперсия для 2 группы:
Таблица 5.3
|
|
|
|
| 2,004039924 | 0,24186206 | 0,05849726 |
| 1,631061138 | -0,131116726 | 0,0171916 |
| 1,866944243 | 0,104766379 | 0,01097599 |
| 1,576653013 | -0,185524851 | 0,03441947 |
| 1,783614589 | 0,021436725 | 0,00045953 |
| 1,710754278 | -0,051423586 | 0,00264439 |
| Итого: | - | 0,12418823 |
![]()
Дисперсия для 3 группы:
Таблица 5.4
|
|
|
|
| 2,141579732 | 0,005654493 | 3,19733E-05 |
| 2,048149263 | -0,087775976 | 0,007704622 |
| 2,184264218 | 0,048338979 | 0,002336657 |
| 2,1524932 | -0,173745039 | 0,030187338 |
| 2,084616778 | -0,051308461 | 0,002632558 |
| 2,394761242 | 0,258836003 | 0,066996077 |
| Итого: | - | 0,073939878 |
![]()
Дисперсия для 4 группы:
Таблица 5.5
|
|
|
|
| 2,60467652 | -0,056404872 | 0,00318151 |
| 2,740513813 | 0,07943242 | 0,006309509 |
| 2,638053845 | -0,023027548 | 0,000530268 |
| Итого: | - | 0,010021287 |
![]()
Далее я рассчитываю среднюю внутригрупповую дисперсию :
Внутригрупповая дисперсия находится по формуле:
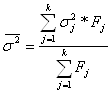
![]()
Далее я рассчитываю межгрупповую дисперсию:
Межгрупповая дисперсия рассчитывается по формуле:

Таблица 5.6
| № | Кол-во |
|
|
|
|
| 1 | 10 | 1,229907691 | -0,5245424 | 0,275144748 | 2,751447479 |
| 2 | 6 | 1,762177864 | 0,00772776 | 0,000059718 | 0,000358309 |
| 3 | 6 | 2,167644072 | 0,41319396 | 0,170729252 | 1,024375512 |
| 4 | 3 | 2,661081393 | 0,90663128 | 0,821980286 | 2,465940859 |
| Итого: | 25 | - | - | - | 6,242122159 |
![]()
Далее рассчитываю общую дисперсию:
![]()
Рассчитываю коэффициент детерминации:
![]()
Рассчитываю эмпирическое корреляционное отношение:
![]()
Изменение фонда заработной платы влияет на изменение фондоотдачи основных фондов на 56,4%, между фондом заработной платы и фондоотдачей основных фондов предприятия существует тесная положительная связь.
6. Определение тесноты взаимосвязи между показателями с помощью коэффициента ранговой корреляции
Коэффициент ранговой корреляции находится по формуле:

Таблица 6.1
| № | Фонд заработной платы, млн.р. | Фондоотдача основных фондов | Ранг ФЗП | Ранг Ф | dk | d2k |
| 1 | 33,6 | 0,909494725 | 1 | 5 | -4 | 16 |
| 2 | 63,2 | 0,803056027 | 3 | 3 | 0 | 0 |
| 3 | 241 | 2,004039924 | 16 | 15 | 1 | 1 |
| 4 | 275,3 | 2,141579732 | 19 | 18 | 1 | 1 |
| 5 | 159,7 | 1,631061138 | 12 | 10 | 2 | 4 |
| 6 | 209 | 1,866944243 | 15 | 13 | 2 | 4 |
| 7 | 251,8 | 2,048149263 | 17 | 16 | 1 | 1 |
| 8 | 286,3 | 2,184264218 | 21 | 20 | 1 | 1 |
| 9 | 149,3 | 1,576653013 | 11 | 9 | 2 | 4 |
| 10 | 93,4 | 0,8 | 9 | 2 | 7 | 49 |
| 11 | 406,9 | 2,60467652 | 23 | 22 | 1 | 1 |
| 12 | 80,6 | 1,9621802 | 7 | 14 | -7 | 49 |
| 13 | 278,2 | 2,1524932 | 20 | 19 | 1 | 1 |
| 14 | 70,9 | 0,811379097 | 4 | 4 | 0 | 0 |
| 15 | 92 | 1,238848108 | 8 | 8 | 0 | 0 |
| 16 | 260,8 | 2,084616778 | 18 | 17 | 1 | 1 |
| 17 | 71,6 | 1,092422251 | 5 | 7 | -2 | 4 |
| 18 | 191 | 1,783614589 | 14 | 12 | 2 | 4 |
| 19 | 450,9 | 2,740513813 | 25 | 24 | 1 | 1 |
| 20 | 120,5 | 2,988864143 | 10 | 25 | -15 | 225 |
| 21 | 79,7 | 0,768774704 | 6 | 1 | 5 | 25 |
| 22 | 175,5 | 1,710754278 | 13 | 11 | 2 | 4 |
| 23 | 38,1 | 0,92405765 | 2 | 6 | -4 | 16 |
| 24 | 417,4 | 2,638053845 | 24 | 23 | 1 | 1 |
| 25 | 343,9 | 2,394761242 | 22 | 21 | 1 | 1 |
| Итого: | 4840,6 | 43,8612527 | - | - | - | 414 |
![]()
7. Определение тесноты парной связи и формы связи с использованием корреляционно- регрессивного анализа между признаками
Тесноту парной связи и форму связи с использованием корреляционно-регрессивного анализа я определяю между фондом заработной платы и фондоотдачей основных фондов.
7.1 Определение тесноты парной связи и формы для всей статистической совокупности 7.1.1Линейная форма зависимости![]()
Таблица 7.1
| № | x | y | Xy | x2 | y2 | Yx |
| 1 | 33,6 | 0,909494725 | 30,55902277 | 1128,96 | 0,827180655 | 1,046650876 |
| 2 | 63,2 | 0,803056027 | 50,75314092 | 3994,24 | 0,644898983 | 1,177574095 |
| 3 | 241 | 2,004039924 | 482,9736217 | 58081 | 4,016176017 | 1,963998029 |
| 4 | 275,3 | 2,141579732 | 589,5769001 | 75790,09 | 4,586363747 | 2,115709732 |
| 5 | 159,7 | 1,631061138 | 260,4804638 | 25504,09 | 2,660360437 | 1,604401483 |
| 6 | 209 | 1,866944243 | 390,1913469 | 43681 | 3,485480808 | 1,822459413 |
| 7 | 251,8 | 2,048149263 | 515,7239844 | 63403,24 | 4,194915402 | 2,011767312 |
| 8 | 286,3 | 2,184264218 | 625,3548457 | 81967,69 | 4,771010175 | 2,164363632 |
| 9 | 149,3 | 1,576653013 | 235,3942949 | 22290,49 | 2,485834725 | 1,558401433 |
| 10 | 93,4 | 0,8 | 74,72 | 8723,56 | 0,64 | 1,311151164 |
| 11 | 406,9 | 2,60467652 | 1059,842876 | 165567,61 | 6,784339776 | 2,69778729 |
| 12 | 80,6 | 1,9621802 | 158,1517241 | 6496,36 | 3,850151138 | 1,254535717 |
| 13 | 278,2 | 2,1524932 | 598,8236083 | 77395,24 | 4,633226978 | 2,128536669 |
| 14 | 70,9 | 0,811379097 | 57,52677798 | 5026,81 | 0,658336039 | 1,211631825 |
| 15 | 92 | 1,238848108 | 113,974026 | 8464 | 1,534744636 | 1,304958849 |
| 16 | 260,8 | 2,084616778 | 543,6680558 | 68016,64 | 4,345627113 | 2,051575047 |
| 17 | 71,6 | 1,092422251 | 78,2174332 | 5126,56 | 1,193386375 | 1,214727982 |
| 18 | 191 | 1,783614589 | 340,6703865 | 36481 | 3,181281002 | 1,742843942 |
| 19 | 450,9 | 2,740513813 | 1235,697678 | 203310,81 | 7,510415958 | 2,892402886 |
| 20 | 120,5 | 2,988864143 | 360,1581292 | 14520,25 | 8,933308863 | 1,431016679 |
| 21 | 79,7 | 0,768774704 | 61,27134387 | 6352,09 | 0,591014545 | 1,250554944 |
| 22 | 175,5 | 1,710754278 | 300,2373759 | 30800,25 | 2,926680201 | 1,674286175 |
| 23 | 38,1 | 0,92405765 | 35,20659645 | 1451,61 | 0,85388254 | 1,066554744 |
| 24 | 417,4 | 2,638053845 | 1101,123675 | 174222,76 | 6,95932809 | 2,744229648 |
| 25 | 343,9 | 2,394761242 | 823,5583913 | 118267,21 | 5,734881408 | 2,41913314 |
| Итого: | ||||||
| 4840,6 | 43,8612527 | 10123,8557 | 1306063,56 | 88,00282561 | 43,8612527 | |

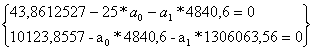
![]()

![]()
Рисунок 7.1
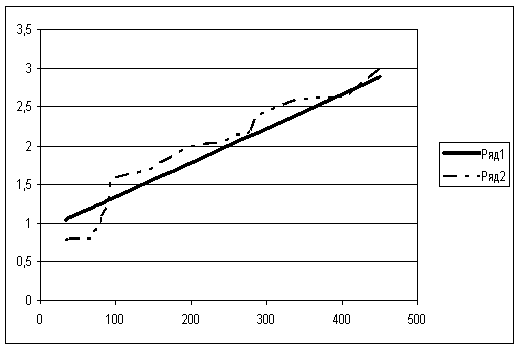
![]()
Таблица 7.2
| № | x | y | lgx | lgy | lgxlgy | (lgx)2 | Yx |
| 1 | 33,6 | 0,909494725 | 1,5263393 | -0,041199815 | -0,062884896 | 2,32971159 | 0,7631503 |
| 2 | 63,2 | 0,803056027 | 1,8007171 | -0,095254154 | -0,171525782 | 3,242581996 | 1,0420802 |
| 3 | 241 | 2,004039924 | 2,382017 | 0,301906369 | 0,719146117 | 5,674005191 | 2,0161849 |
| 4 | 275,3 | 2,141579732 | 2,4398062 | 0,330734248 | 0,806927473 | 5,952654349 | 2,1529068 |
| 5 | 159,7 | 1,631061138 | 2,2033049 | 0,21247024 | 0,468136725 | 4,854552553 | 1,6459264 |
| 6 | 209 | 1,866944243 | 2,3201463 | 0,271131348 | 0,62906439 | 5,383078789 | 1,8794161 |
| 7 | 251,8 | 2,048149263 | 2,4010557 | 0,311361603 | 0,747596561 | 5,765068598 | 2,0602409 |
| 8 | 286,3 | 2,184264218 | 2,4568213 | 0,339305171 | 0,833612189 | 6,035971136 | 2,1949018 |
| 9 | 149,3 | 1,576653013 | 2,1740598 | 0,197736125 | 0,429890162 | 4,726536048 | 1,5921726 |
| 10 | 93,4 | 0,8 | 1,9703469 | -0,096910013 | -0,190946341 | 3,882266813 | 1,2634054 |
| 11 | 406,9 | 2,60467652 | 2,6094877 | 0,415753795 | 1,08490441 | 6,809426003 | 2,6103113 |
| 12 | 80,6 | 1,9621802 | 1,906335 | 0,292738889 | 0,558058402 | 3,634113292 | 1,1748423 |
| 13 | 278,2 | 2,1524932 | 2,4443571 | 0,332941788 | 0,813828632 | 5,974881758 | 2,1640595 |
| 14 | 70,9 | 0,811379097 | 1,8506462 | -0,090776185 | -0,167994605 | 3,424891488 | 1,10286 |
| 15 | 92 | 1,238848108 | 1,9637878 | 0,093018062 | 0,182667738 | 3,856462631 | 1,2540319 |
| 16 | 260,8 | 2,084616778 | 2,4163076 | 0,319026229 | 0,770865497 | 5,838542355 | 2,0962277 |
| 17 | 71,6 | 1,092422251 | 1,854913 | 0,038390538 | 0,071211108 | 3,44070232 | 1,1082156 |
| 18 | 191 | 1,783614589 | 2,2810334 | 0,251301016 | 0,573226003 | 5,203113222 | 1,7977819 |
| 19 | 450,9 | 2,740513813 | 2,6540802 | 0,437831995 | 1,162041245 | 7,044141895 | 2,745871 |
| 20 | 120,5 | 2,988864143 | 2,080987 | 0,475506175 | 0,989522191 | 4,330507089 | 1,4325096 |
| 21 | 79,7 | 0,768774704 | 1,9014583 | -0,114200916 | -0,217148281 | 3,615543748 | 1,1683554 |
| 22 | 175,5 | 1,710754278 | 2,2442771 | 0,233187635 | 0,523337674 | 5,036779795 | 1,7243012 |
| 23 | 38,1 | 0,92405765 | 1,580925 | -0,034300933 | -0,054227202 | 2,499323779 | 0,8119427 |
| 24 | 417,4 | 2,638053845 | 2,6205524 | 0,421283656 | 1,103995914 | 6,867295116 | 2,6433103 |
| 25 | 343,9 | 2,394761242 | 2,5364322 | 0,379262221 | 0,9619729 | 6,433488183 | 2,4025357 |
| Итого: | |||||||
|
| 4840,6 | 43,8612527 | 54,620195 | 5,182245088 | 12,56527822 | 121,8556397 | 42,847542 |

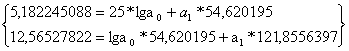
![]()
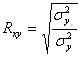
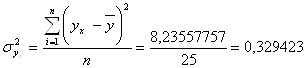
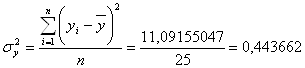
![]()
Рисунок 7.2
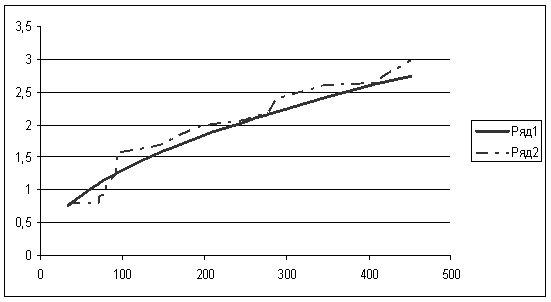
Таблица 7.3
| № | X | Y | XY | X2 | Y2 | Yx |
| 1 | 85,7625 | 1,229908 | 105,479985 | 7355,206406 | 1,51267369 | 1,2471831 |
| 2 | 190,0875 | 1,762178 | 334,968011 | 36133,25766 | 3,1052713 | 1,7139097 |
| 3 | 294,4125 | 2,135925 | 628,843019 | 86678,72016 | 4,56217561 | 2,1806363 |
| 4 | 398,7375 | 2,661081 | 1061,07279 | 158991,5939 | 7,08135209 | 2,6473629 |
| Итого: | ||||||
| 969 | 7,789092 | 2130,3638 | 289158,7781 | 16,2614727 | 7,789092 | |

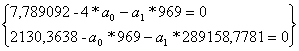
![]()

![]()
Рисунок 7.3
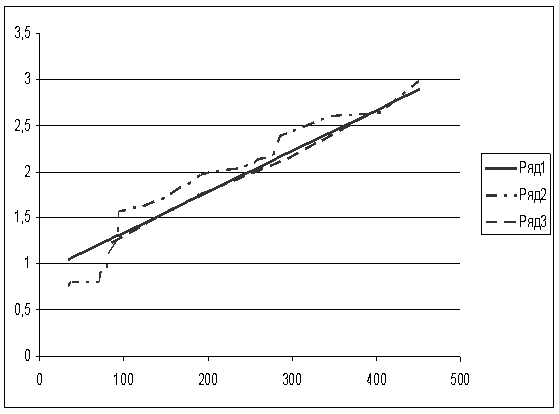
При сравнении пунктов 7.1 и 7.2 видно, что в обоих пунктах коэффициент корреляции достаточно велик, что свидетельствует о сильной и прямой связи между фондом заработной платы и фондоотдачей основных фондов.
Похожие работы
... статистической информации на ЭВМ. 3. Организация решения статистических задач с помощью комплекса средств новой технологии для обработки статистической информации. Одной из главных особенностей автоматизированной обработки статистической информации является новая технология, обеспечиваю- щая более эффективную обработку на основе достижения технической, программной, ...
... ) опытных значений показателя надежности на генеральную совокупность: (1.40) 1.9 Определение минимального числа объектов наблюдения при оценке показателей надежности Точность определения показателей надежности зависит при прочих равных условиях от объема информации, т.е. от числа испытуемых объектов. Как известно, с увеличением количества испытуемых объектов N доверительные границы ...
... показателях отражаются сведения о причинах выбытия (окончания срока договора, переходя на учебу, по собственному желанию и т.п.). В целях углубленного статистического анализа движения рабочей силы их целесообразно дополнить группировками, которые давали бы необходимую информацию для планирования, анализа актуальных кадровых вопросов. Например, из всех причин выбытия работников с прежнего места ...
... Одним из направлений многогранной деятельности статистического аппарата ОН - Статистической комиссии и Статистического Бюро является исследование международной торговли. Важнейшими аспектами этой работы всегда были: с одной стороны, сбор, обработка и публикация статистической информации о внешней торговле отдельных государств мира и расчёт показателей мировой торговли, с другой - стандартизация и ...

0 комментариев