Расчет сил в элементах фермы

2.  расчет сил в элементах фермы

 

Ферма наружается осевой F₁ и поперечной F₂ силами. Усилие в отдельном стержне от осевой силы

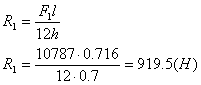 (2.1)

При вычислении усилий в стержне от поперечной силы F₂ полагаем, что нагрузку воспринимают только те стержневые треугольники (рис.2.), плоскость которых параллельна плоскости действия силы F₂.  

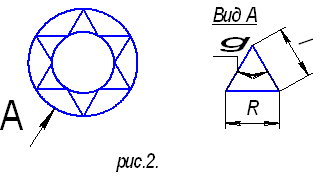
Тогда усилие в отдельном стержне

 (2.2)

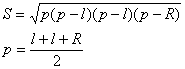где  (2.3)

Предположим, что усилия от F₁ и F₂ складываются в одном стержне по максимуму

независимо от направления их действия:

 (2.4)

Найдем напряжение:

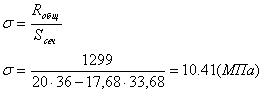 (2.5)

3.  определение критической нагрузки стержня

 

Потеря устойчивости первоначальной формы равновесия элементов конструкций может оказаться причиной исчерпания их несущей способности и в процессе эксплуатации недопустима. Положение равновесия может быть устойчивым, безразличным (нейтральным) и неустойчивым.

При центральном сжатии стержня с прямолинейной осью, с фиксированной линией действия силы характерны следующие ситуации:

a)  Если Р<P_{кр ,} то при снятии малых поперечных возмущений продольная ось стержня стремится вернуться к исходному прямолинейному положению равновесия.

b)  При Р=Р_кр возможно множество форм равновесия – прямолинейная и близкие к ней мало деформированные, что соответствует безразличному положению равновесия. При этом исходная прямолинейная форма равновесия стержня перестает быть устойчивой. Нагрузка Р= Р_кр, при которой прямолинейная форма равновесия перестает быть устойчивой, называется критической.

c)  При Р>Pкр прямолинейное положение оси стержня статически возможно, но неустойчиво.

Для определения критической силы для сжатого стержня при различных условиях закрепления (различных граничных условиях) воспользуемся формулой Эйлера:

(3.1)

где μ – коэффициент приведенной длины, показывающий во сколько раз нужно изменить длину шарнирно опертого стержня, чтобы критическая сила для него равнялась критической силе для стержня длиной l при рассматриваемых граничных условиях.

Для шарнирно опертого стержня μ=1.

Найдем длину стержней

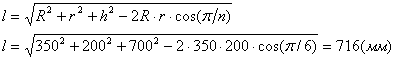 (3.2)

где R – радиус верхнего шпангоута

r – радиус нижнего шпангоута

h – высота конструкции

n – количество узлов.

 Найдем момент инерции сечения стержня:

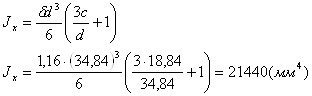 (3.3)

Подставим найденные значения в формулу Эйлера (3.1) и получим критическую силу

Найдем критические напряжения:

 (3.4)

4.  определение коэффициента запаса прочности. Определение массы

Найдем коэффициент запаса прочности

(4.1)

Найдем массу фермы без учета распорных шпангоутов

(4.2)

где

 (4.3)

 

Подставим (4.3) в (4.2)

 (4.4)