Навигация
Создание рабдологии (изобретение палочек Непера)
2. Создание рабдологии (изобретение палочек Непера).
Термин «рабдология» Непер объяснял как «счет с помощью палочек» (впоследствии этим термином воспользовался К. Перро). Эти палочки под названием «палочек Непера», как и сам метод умножения с их помощью, быстро получили распространение в Европе и были одно время даже более популярны, чем логарифмы – главное изобретение Непера.
Счетную доску (или просто лист чистой бумаги) расчеркивали в виде сетки прямоугольников, разделенных диагоналями. По сторонам сетки (сверху и справа) записывали сомножители, а промежуточные произведения помещали в треугольники так, чтобы диагональ разделяла единицы и десятки (единицы помещались в нижний треугольник, а десятки – в верхний). Для получения произведений осуществляли суммирование «вдоль диагоналей», а результат записывали снизу сетки (младшие разряды) и слева от сетки (старшие разряды).
Непер предложил разрезать «школьную» таблицу умножения на 10 полосок (включая нулевую) и числа разделить диагональю на единицы и десятки. Полоски наклеивались на деревянные палочки и использовались следующим образом.
Пусть требуется умножить 2085 на 4. Для этого брали палочки для цифр 2, 0, 8 и 5 и еще одну – единичную. Против цифры 4 единичной палочки искали произведение 4 на цифры 2, 0, 8 и 5, из которых составлено множимое.
Суммируя числа как в «gelosia», получаем:
2085 * 4 = 8; (0 + 3); (2 + 2); 0; = 8340.
Таким образом, каждая палочка имела на противолежащих гранях полоски для некоторой цифры и ее дополнения до девяти.
С помощью «палочек Непера» можно было выполнять не только операцию умножения, но и деления извлечения квадратного корня.
3.Усовершенствования палочек Непера – два направления
3.1. Работы Женейема и Люка
Палочки Непера неоднократно усовершенствовались. Это совершенствование шло в двух направлениях и оказало определенное влияние на последующий ход развития вычислительной техники.
Первое направление развивалось в рамках домеханических вычислительных средств. По существу, это те же палочки Непера, точно так же перекладываемые ручным способом но отличающиеся формой (бруски, полоски и т. п.). второе направление – это механические вычислительные устройства, в которых выполнение операции умножения базировалось на той или иной форме использования палочек Непера.
Первую идею усовершенствования счетных палочек дал их изобретатель. В первом приложении к «рабдологии» Непера содержится описание набора из 200 счетных палочек, позволяющего сразу производить умножение многозначных чисел на многозначные. Пользование таким набором более сложно, чем обычным набором счетных палочек, и неэффективно при перемножении небольших чисел. Однако если разрядность сомножителей велика (Непер приводит пример 8 795 036 412 * 3 586 290 741 = 31 541 557 651 113 461 292), то использование такого прибора ускоряет вычисления.
Наиболее остроумная модификация была предложена в 1885 году двумя французскими изобретателями: железнодорожным инженером Женейном и сотрудником Музея искусств и ремесел Эдуардом Люка. Набор Женейя и Люка содержал 11 брусков. Один из них, соответствующий множителю, имел боковую грань, разделенную на два вертикальных столбца. Левый столбец разбит на 8 клеток с цифрами 2, 3, …, 9, означающими множитель. Правый столбец разбивался на различное число клеток в зависимости от множителя; против множителя 2 были две клетки с цифрами 0, 1, против множителя 3 - три клетки с цифрами 0, 1, 2 и т. д.
У остальных 10 брусков использовались все четыре боковые грани. Каждая их них также разбивалась на два вертикальных столбца. В самом верху грани справа была написана цифра множимого. Далее правая колонка разбивалась на клетки так же, как и на бруске, написанном выше.
Произведение однозначных чисел записывается так: верхняя клетка правой колонки содержит цифру единиц произведения; в следующих клетках пишутся соседние цифры в порядке возрастания. Цифра десятков изображается в левой колонке с помощью черного треугольника, вершина которого находится на высоте нужной клетки. Благодаря этому, читая цифры результата против вершин, мы избавляемся от необходимости сложения для получения нужных значений разрядов.
Второе направление совершенствования палочек Непера имеет место в рамках механической вычислительной техники.
3.2. «Математический орган» Кирхера и Шотта. Жизнь и деятельность этих ученых
Этот удивительный XVII век! Век замечательных открытий и изобретений, век становится современной науки, век математический, век, когда трудами Фрэнсиса Бэкона и Рене Декарта естествознание начало освобождаться от пут теологии; век, когда были созданы маятниковые часы и морской хронометр, микроскоп, телескоп, термометр, ртутный барометр, гигрометр, счетная машина… XVII век – век Галилео Галилея, Иоганна Кеплера, Исаака Ньютона, Вильгельма Лейбница, Блеза Паскаля, Джона Непера, братьев Бернулли, Христиана Гюйгенса, Роберта Гуака, Антона Левенгука, Роберта Бойля, Жозефа Савера и многих, многих других. В XVII веке появляются первые академии наук - Флорентийская академия опытов (1657 г.), Лондонское Королевское общество (1662 г.), Парижская академия наук (1666 г.); первые государственные обсерватории – в Париже (1672 г.) и Гринвиче (1675 г.); первые научные журналы – французский «Журнал ученых» (1665 г.), английский «Философские труды» (1665 г.).
«Ах, люди XVII века! Как основательно они все знали! Как медленно читали!» (Густав Флобер).
Люди XVII века знали все «основательно», но еще не всегда могли отличать зерна от плевел. Вот почему в то время, когда Роберт Бойль создавал основы научной химии, еще дымились реторты в лабораториях алхимиков; «отец» научной геологии датчанин Н. Стенсен пытался связать свою геологическую историю земли с библейским потопом; гениальный астроном Кеплер составлял гороскопы; великие математики Непер и Ньютон вычисляли день «Страшного суда» и прихода Антихриста, а книги наряду с научным содержанием были полны описаниями невероятных событий, диковинных фактов и неожиданных изобретений…
Весьма показательны в этом отношении книги двух отцов – иезуитов - Афанасия Кирхера и Каспара Шотта, трудолюбивых исследователей и неутомимых сочинителей. «Кирхер был человеком, обладавшим необыкновенной эрудицией, но не любившим тщательного обдумывания и не терпевших критики», - писал один из его биографов. «Он был одарен очень смелым воображением, обширной памятью и колоссальным терпением, но несмотря на это ему не удалось» проверить все факты, изложенные в его книгах». А вот мнение о трудах Шотта французского писателя и ученого Мерсье де Сент – Леже (1785 г.): «Я знаю, эти сочинения не свободны от недостатков; их автор, если хотите, перегружен множеством бесполезных, случайных и смешных вещей, но там можно найти любопытные факты, драгоценные наблюдения, опыты, заслуживающие внимания; они могу указать дорогу к открытиям тех, кто будет иметь смелость копаться в этой шахте…»
В 1688 году была опубликована (после смерти автора) книга Каспара Шотта «Математический инструмент», в которой содержалось описание множительного устройства, изобретенного, по – видимому, его другом Анасиусом Кирхером.
Конструкция прибора Кирхера – Шотта практически идентична конструкциям Шиккарда и Грийе. Только в «математическом инструменте» 9 цилиндров с навернутыми на них таблицами, что позволяло увеличить длину множимого до 9 десятичных разрядов. Не следует, однако, забывать, что конструкция Шиккарда была, по всей вероятности, не известна Кирхеру и Шотту, а машина Грийе появилась позже (во всяком случае, с публикацией о ней Шотт не был знаком: книга Грийе вышла в свет через 7 лет после смерти Шотта).
Жизненные пути Афанасия Кирхера и Каспара Шотта, то пересекавшиеся между собой, то расходившиеся, характерны для «кабинетных» ученых XVII столетия, которые в первую часть жизни учились сами, а во вторую – учили других.
Афанасий Кирхер родился 2 мая 1601 года в Гейсене, он был девятым ребенком доктора теологии Иоганна Кирхера. До 11 лет посещал гейсенскую начальную школу и, кроме того, занимался с отцом музыкой, латынью и географией. В 1612 году мальчика перевели в иезуитское училище при старинном монастыре Фульда, а еще через шесть лет, после вступления Кирхера в Орден Иисуса, его зачислили в иезуитский колледж в Падеборне. Здесь он изучал математику, физику, логику, философию и языки – греческий и древнееврейский.
В 1623 году Кирхер начинает свою преподавательскую деятельность в качестве учителя греческого языка в Эйхсфельде, но затем вновь в течение 1624 – 1627 годов изучает теологию в Майнце. По педагогической традиции иезуитов, в соответствие с которой последний год студент обязан провести в стенах другого училища. Кирхер переводится в 1628 году в Шнеер, где и получает сан священника. В следующем году он зачисляется профессором математики, философии и восточных языков Вюрцбургского университета. Одним из его студентов и восторженным почитателем был 23 – летний иезуит Каспар Шотт, с которым молодого профессора связала крепкая дружба.
Вскоре, однако, Тридцатилетняя война вмешалась в жизнь университета: после победного сражения у Брейтенфельда шведский король Густав – Адольф в октябре 1631 года занял Вюцбург. Кирхер бежит во Францию, где в Авиньоне продолжает свою педагогическую деятельность, а Шотт находит прибежище в одном из итальянских иезуитских колледжей.
В 1663 году Кирхер стал профессором римской высшей школы иезуитов (Коллегио Романо). Последующие годы вплоть до смерти, наступившей 27 ноября 1680 года, он жил почти безвыездно в Риме.
Шотт после окончания колледжа долгие годы преподавал моральную теологию и математику в Палермо, в 1651 – 1653 годах был ассистентом Кирхера в Коллегио Романо, а затем профессором математики и физики в иезуитской школе родного Вюцбурга.
Умер Каспар в 1666году.
Из–под трудолюбивых перьев Кирхера и Шотта вышло большое количество пухлых фолиантов – учебников, монографий по отдельным вопросам науки и техники и просто пестрых собраний фактов, рассказов, домыслов. Заметим, что все сочинения Шотта могут рассматриваться в основе своей как сокращенное изложение рукописей Кирхера.
Какие только вопросы в них не затронуты!
Арифметика, геометрия, тригонометрия, алгебра, учение о логарифмах, астрономия, хронография, география, акустика, диоптрика и катоптрика, механика, статика, гидрология, гидротехника, пиротехника, криптография, фортификация, топография, химия, архитектура, строительная механика, музыка, телескоп, микроскопы, трубы для тугоухих, магниты и их свойства, гидравлические органы, автоматы, пневматические машины, водолазные колокола, военная тактика и стратегия и т. д. Но, кроме того, там говорилось об астрологии, о симпатиях между неодушевленными телами, о вечных двигателях, о медицинском чародействе, о физиогномике, о различных видах гадания, об ангелах и демонах, привидениях и кентаврах, сатирах, нимфах и великанах, бесноватых, ликан – тропах, о фокусах с картами и стаканами, о редких медицинских рецептах, о статуях, которые говорят и двигаются, о палингенезе – способе воскрешения растений из пепла и пр.
Иногда среди вороха сведений блеснет «алмазное зерно»: первые удачные попытки расшифровки египетских иероглифов, «блошиное стекло» - нехитрый увеличительный прибор с двояковыпуклой линзой, изобретенный Кирхером в 1666645 году; первое описание воздушного насоса Отто фон Герике, помещенное с согласия автора в одну из книг Шотта; рупор – громкоговоритель – здесь Кирхер оспаривал авторство с Сэмюэлем Морлендом, наконец первая попытка механизации «неперовских палочек» - прибор, изобретенный, вероятно, Кирхером, но популярно описанный Шоттом в книге «Organum mathematicum» (1668 г.).
Таким образом, в приборе Кирхера – Шотта был «механизирован» процесс подбора «палочек» для представления необходимого множимого и расширен диапазон «представимых чисел».
Похожие работы
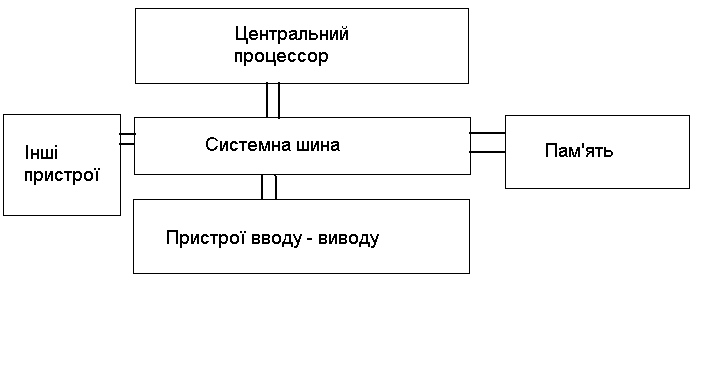
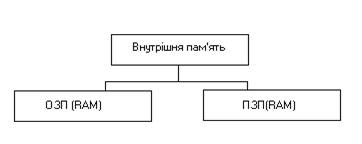
... що в свою чергу впливає на бажання випуску світовими виробниками периферійних пристроїв сумісних з IBM - стандартом. Основні пристрої Материнська плата, вона ж і Motherboard або Mainboard – це найосновніша частина IBM -сумісних ПК . На ній знаходиться процессор, BIOS, системна шина, інтерфейси, пам’ять. Іноді з метою здешевлення в неї встроюють ( інтегрують ) такі пристрої як ...
... объявлено о намерении компании увеличить свою прибыль на 2 718 281 828 долларов. Заявленное число представляет собой первые 10 цифр известной математической константы. В языках программирования символу e в экспоненциальной записи чисел соответствует число 10, а не Эйлерово число. Это связано с историей создания. Ссылки: История числа e (англ.) e for 2.71828… (англ.) (история и правило Джексона ...
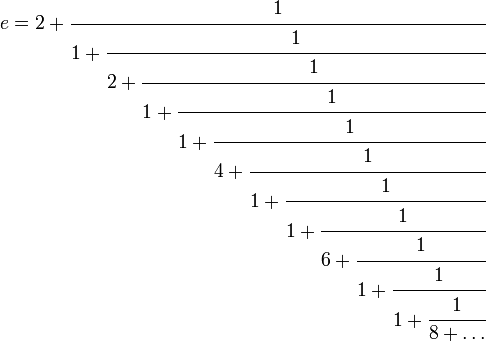
0 комментариев