Навигация
Разработка печатного модуля РЭС с использованием учебных алгоритмов САПР
Министерство образования Республики Беларусь
Белорусский государственный университет информатики и радиоэлектроники
Факультет компьютерного проектирования
Кафедра радиоэлектронных средств
Пояснительная записка
к курсовому проекту
по предмету: «Автоматическое конструирование и технология проектирования РЭС»
на тему:
«Разработка печатного модуля РЭС с использованием учебных алгоритмов САПР»
Выполнил:
студент группы 810202
Воронович А.В.
Минск 2000
Содержание
Введение
1. Решение задачи компоновки для функциональной схемы с использованием последовательного алгоритма
1.1 Общее описание алгоритма
1.2 Пошаговое описание алгоритма
1.3 Выполнение компоновки
2. Размещение элементов в принципиальной электрической схеме с использованием последовательного алгоритма
2.1 Краткое описание алгоритма последовательной установки элементов РЭА2.2 Выполнение размещения
2.3 Результаты размещения
3. Трассировка цепей питания и земли с использованием алгоритма построения кратчайших связывающих сетей и волнового алгоритма
3.1 Краткое описание алгоритма Краскала
3.2 Трассировка цепей земли по алгоритму Краскала
3.3 Трассировка цепей питания по алгоритму Прима
4. Трассировка сигнальных цепей с помощью волновых алгоритмов
Заключение
Список используемой литературы
Введение
Стремление разработать эффективные методы конструирования РЭА, позволяющие обобщить опыт работы высоко квалифицированных конструкторов и сделать их достаточно универсальными, приводит к необходимости формализации процесса конструирования.
Разработанная обобщённая модель конструкции РЭА подвергается тщательным исследованиям с точки зрения удовлетворения параметров конструкций заданным техническим требованиям.
Успешное решение формализации конструкторской деятельности возможно лишь только при её алгоритмизации и автоматизации с использованием математических методов, теории графов, алгоритмов, математического программирования и исследование операции, методов вычислительной математики.
Следует отметить, что в общем случае процессы конструирования РЭА плохо поддаются формализации и с математической точки зрения относятся к так называемым плохо формализуемым задачам. Тем не менее для широкого круга задач удалось найти математическое описание и на его основе построить алгоритмы и программы их решения на ЭВМ.
В настоящее время на основе современных вычислительных комплексов и средств автоматизации созданы и находятся в промышленной эксплуатации схемы автоматизированного проектирования РЭА и ЭВА, позволяющие в значительной степени освободить конструктора-проектировщика от однообразной, трудоёмкой и утомительной умственной работы и повысить его интеллектуальные возможности на этапах принятия решений.
Существующие системы автоматизированного проектирования РЭА решают комплекс вопросов по проектированию схем и конструкций аппаратуры.
Нам необходимо разработать печатный модуль РЭС с использованием учебных алгоритмов САПР.
1. Решение задачи компоновки 1.1 Общее описание алгоритма
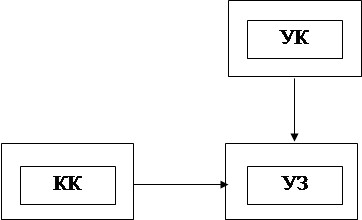
Общая схема процесса последовательной компоновки по связности имеет следующий вид:
Пусть дана схема соединения элементов из множества ![]() . Определим последовательный процесс назначения элементов
. Определим последовательный процесс назначения элементов ![]() в узлы Br(
в узлы Br(![]() ), на каждом шаге которого выбирается один из неразделенных элементов и приписывается очередному узлу.
), на каждом шаге которого выбирается один из неразделенных элементов и приписывается очередному узлу.
Узел считается завершенным, если число элементов в узле равно заданному числу K.
После завершения очередного узла аналогичная процедура повторяется для следующего узла, причем кандидатами для назначения являются элементы, не включенные в предыдущие узлы. Процесс заканчивается, когда все элементы из множества E распределены.
Исходные данные являются:
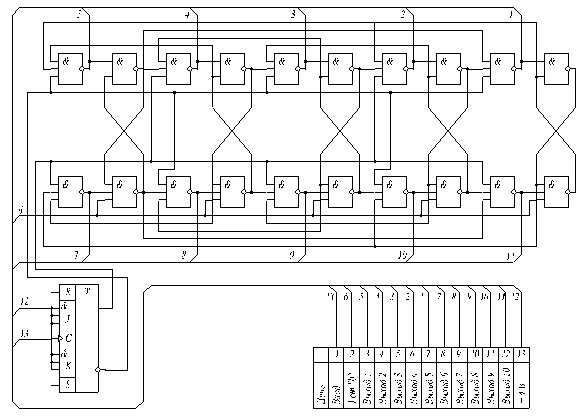
– электрическая схема устройства (Рис.1);
– максимально допустимое число элементов в модуле.
Электрическую схему удобно представлять графом G=(E,V), где множество вершин Е соответствует элементам электрической схемы, а множество ребер V –электрическим связям между элементами.
В таком виде задача компоновки может быть сформулирована как задача разрезания графа
G=(E,V) на множество подграфов
Gr = (Er, Vr),
где r=1, 2, 3…![]() .
.
В каждом подграфе число вершин соответственно Er должно не превосходить ранее заданного ограничения на число элементовв в узле К. Для любого разбиения должны выполняться следующие условия:
 |
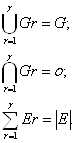 (1)
(1) Рис.1
При проведении компоновки без учета ограничения на кол-во внешних выводов в узле все модули, кроме последнего, будут иметь полное заполнение и последнее условие примет вид
![]() (2)
(2)
Шаг 1.
Формирование очередного подграфа Gr(r=1,2,3…![]() ) начинается с выбора базовой вершины
) начинается с выбора базовой вершины ![]() из множества нераспределенных вершин Ir. В начале процесса все вершины считаются нераспределенными, т.е. Ir=E.
из множества нераспределенных вершин Ir. В начале процесса все вершины считаются нераспределенными, т.е. Ir=E.
Критерием выбора вершины на роль базовой является ее степень ![]() (
(![]() ) (под степенью вершины графа будем понимать кол-во ребер данного графа, инцидентных ей). Выбор происходит в соответствии со следующим условием:
) (под степенью вершины графа будем понимать кол-во ребер данного графа, инцидентных ей). Выбор происходит в соответствии со следующим условием:
![]()
![]()
![]() (3)
(3)
Базовая вершина будет первой по порядку вершиной подграфа Gr(Er,Vr), а оставшиеся вершины, принадлежащие множеству ![]() , являются кандидатами для включения в подграф Gr на последующих шагах алгоритма.
, являются кандидатами для включения в подграф Gr на последующих шагах алгоритма.
Базовая вершина ![]() является, во-первых, как бы “центром” группирования, к которому прибавляются новые вершины, во-вторых, центром факторизации.
является, во-первых, как бы “центром” группирования, к которому прибавляются новые вершины, во-вторых, центром факторизации.
Шаг 2.
Из множества ![]() выделяется подмножество Г (
выделяется подмножество Г (![]() ) вершин, связанных с
) вершин, связанных с ![]() .
.
Шаг 3.
Для элемента X![]() введем функционал:
введем функционал:
L(x)=![]() (4)
(4)
определяющий число цепей, связывающих вершину X и вершины из множества Г и Ir\![]() .
.
Для упрощения записей будем отождествлять элемент (множество элементов). Для формального вычисления функционала будем пользоваться формулой:
![]() (5)
(5)
где ![]() – число связей между вершинами
– число связей между вершинами ![]() и
и ![]() .
.
Шаг 4.
Из всех вершин ![]() выбирается
выбирается ![]() такая, у которой значение функционала минимально. Очевидно, что вершина, для которой это условие будет выполняться, максимально связана с
такая, у которой значение функционала минимально. Очевидно, что вершина, для которой это условие будет выполняться, максимально связана с ![]() . Эта вершина включается во множество Еr вершин Gr.
. Эта вершина включается во множество Еr вершин Gr.
Множество вершин подграфа Gr приобретает следующий вид:
![]() (6)
(6)
где ![]() , а верхний индекс в обозначении
, а верхний индекс в обозначении ![]() в общем случае указывает кол-во шагов выборки.
в общем случае указывает кол-во шагов выборки.
Шаг 5.
Происходит стягивание вершин подграфа Gr в вершину ![]() . Этот процесс далее будем называть факторизацией, вершину
. Этот процесс далее будем называть факторизацией, вершину ![]() – центром факторизации, а количество вершин стянутых в
– центром факторизации, а количество вершин стянутых в ![]() , кроме него самого, – степенью факторизации.
, кроме него самого, – степенью факторизации.
Центр факторизации со степенью факторизации ![]() , отличной от нуля, будем обозначать символом
, отличной от нуля, будем обозначать символом ![]() и называть гипервершиной степени
и называть гипервершиной степени ![]() .
.
После данного процесса множество ![]() преобразуют в одноэлементное множество
преобразуют в одноэлементное множество ![]() содержащее гипервершину степени
содержащее гипервершину степени ![]() .
.
В указанных обозначениях первый процесс факторизации запишется следующим образом:
![]() . (7)
. (7)
В общем случае на ![]() ом шаге выборки все указанные преобразования будут иметь вид:
ом шаге выборки все указанные преобразования будут иметь вид:
![]() . (8)
. (8)
![]() =1,2,3…,Кс-1,где Кс –допустимая мощность множества вершин формируемого подграфа (кол-во элементов в конструктивном узле).
=1,2,3…,Кс-1,где Кс –допустимая мощность множества вершин формируемого подграфа (кол-во элементов в конструктивном узле).
Шаг 6.
Действия, описанные в шагах 2,3,4,5, повторяются до полного заполнения формируемого модуля.
Далее весь процесс повторяется до тех пор, пока не будет сформирован (![]() -1) модуль. Последний же
-1) модуль. Последний же ![]() –й полностью включает в себя множество
–й полностью включает в себя множество ![]() , так как
, так как
![]() . (9)
. (9)
1.3 Выполнение компоновки
Данную электрическую функциональную схему распределителя уровней на 10 каналов (рис. 1) разбиваем на 3 блока. Далее выполняем компоновку для каждого блока, для чего представляем их в виде графов, где множеству вершин соответствуют элементы электрической схемы блока, а множество ребер электрическим связям между этими элементами.
1.3.1 Компоновка первого блока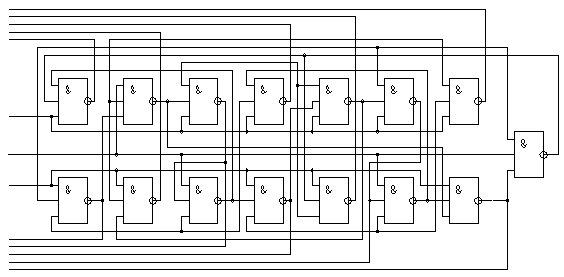
В исходной схеме выделяем однотипные логические элементы. Сведём их в блок 1.
Рис. 2. Блок 1
По блоку 1 составляем граф.
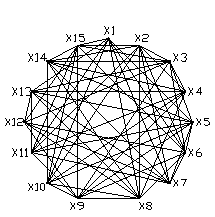 |
Рис. 3. Граф 1
По полученному графу составляем матрицу смежности.
Таблица 1
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | X11 | X12 | X13 | X14 | X15 | ||
| X1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 8 |
| X2 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 9 |
| X3 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 9 |
| X4 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 8 |
| X5 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 9 |
| X6 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 9 |
| X7 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 8 |
| X8 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 9 |
| X9 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 9 |
| X10 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 8 |
| X11 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 8 |
| X12 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 7 |
| X13 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 8 |
| X14 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 8 |
| X15 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 9 |
За базовую принимаем вершину X2, т.к. она имеет максимальное значение, равное 9, и минимальный порядковый номер. Она связана с вершинами X3, X4, X6, X7, X8, X10, X11, X14, X15. Посчитаем для этих вершин функционалы:
L(X1)=8-0=8, L(X3)=9-1=8, L(X4)=8-1=7, L(X5)=9-0=9,
L(X6)=9-1=8, L(X7)=8-1=7, L(X8)=9-1=8, L(X9)=9-0=9, L(X10)=8-1=7, L(X11)=8-1=7, L(X12)=7-0=7, L(X13)=8-0=8, L(X14)=8-1=7, L(X15)=9-1=8.
Стягиваем вершину X4 с базовой в первый корпус, т.к. она имеет минимальный функционал, равный 7, и минимальный порядковый номер.
Таблица 2
| X1 | X3 | X5 | X6 | X7 | X8 | X9 | X10 | X11 | X12 | X13 | X14 | X15 | ||
| X1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 |
| X3 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 2 |
| X5 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 |
| X6 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 |
| X7 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 |
| X8 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 2 |
| X9 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 |
| X10 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 2 |
| X11 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 2 |
| X12 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| X13 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 |
| X14 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 2 |
| X15 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 |
| 0 | 2 | 0 | 1 | 1 | 2 | 1 | 2 | 2 | 0 | 1 | 2 | 1 | 0 |
Стягиваем вершину X7 с X4 и с базовой в первый корпус, т.к. вершина X7 также имеет функционал равный 7.
Таблица 3
| X1 | X3 | X5 | X6 | X8 | X9 | X10 | X11 | X12 | X13 | X14 | X15 | ||
| X1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 |
| X3 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 2 |
| X5 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 |
| X6 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 2 |
| X8 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 2 |
| X9 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 |
| X10 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 2 |
| X11 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 3 |
| X12 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 |
| X13 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 2 |
| X14 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 3 |
| X15 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 2 | 1 | 2 | 2 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 0 |
Так как К155ЛА4 содержит три модуля, элементы X2, X4, X7 помещаем в одну микросхему. Для оставшихся несвязанных элементов будем продолжать компоновку.
Таблица 4
| X1 | X3 | X5 | X6 | X8 | X9 | X10 | X11 | X12 | X13 | X14 | X15 | ||
| X1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 7 |
| X3 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 7 |
| X5 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 8 |
| X6 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 7 |
| X8 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 7 |
| X9 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 8 |
| X10 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 6 |
| X11 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 5 |
| X12 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 6 |
| X13 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 6 |
| X14 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 5 |
| X15 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 8 |
За базовую принимаем вершину X5, т.к. она имеет максимальное значение, равное 8, и минимальный порядковый номер. Она связана с вершинами X1, X3, X6, X9, X10, X11, X13, X14. Посчитаем для этих вершин функционалы:
L(X1)=7-1=6, L(X3)=7-1=6, L(X6)=7-1=6, L(X8)=7-0=7, L(X9)=8-1=7, L(X10)=6-1=5, L(X11)=5-1=4, L(X12)=6-0=6, L(X13)=6-1=5, L(X14)=5-1=4, L(X15)=8-0=8.
Стягиваем вершины X11, X14 с базовой во второй корпус, т.к. они имеют минимальный функционал, равный 4.
Таблица 5
| X1 | X3 | X6 | X8 | X9 | X10 | X12 | X13 | X15 | ||
| X1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 2 |
| X3 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 2 |
| X6 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 |
| X8 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 |
| X9 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 2 |
| X10 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 2 |
| X12 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 |
| X13 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 2 |
| X15 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 2 |
| 2 | 2 | 1 | 1 | 2 | 2 | 0 | 2 | 2 | 0 |
Так как К155ЛА4 содержит три модуля, элементы X5, X11, X14 помещаем в одну микросхему. Для оставшихся несвязанных элементов будем продолжать компоновку.
Таблица 6
| X1 | X3 | X6 | X8 | X9 | X10 | X12 | X13 | X15 | ||
| X1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 5 |
| X3 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 5 |
| X6 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 6 |
| X8 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 6 |
| X9 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 6 |
| X10 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 4 |
| X12 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 6 |
| X13 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 4 |
| X15 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 6 |
За базовую принимаем вершину X6, т.к. она имеет максимальное значение, равное 6, и минимальный порядковый номер. Она связана с вершинами X1, X3, X8, X9, X12, X15. Посчитаем для этих вершин функционалы:
L(X1)=5-1=4, L(X3)=5-1=4, L(X8)=6-1=5, L(X9)=6-1=5, L(X10)=4-0=4, L(X12)=6-1=5, L(X13)=4-0=4, L(X15)=6-1=5.
Стягиваем вершину X1, X3 с базовой в третий корпус, т.к. они имеют минимальный функционал, равный 4.
Таблица 7
| X8 | X9 | X10 | X12 | X13 | X15 | ||
| X8 | 0 | 1 | 1 | 1 | 1 | 0 | 2 |
| X9 | 1 | 0 | 1 | 1 | 0 | 1 | 2 |
| X10 | 1 | 1 | 0 | 0 | 0 | 1 | 1 |
| X12 | 1 | 1 | 0 | 0 | 1 | 1 | 2 |
| X13 | 1 | 0 | 0 | 1 | 0 | 0 | 2 |
| X15 | 0 | 1 | 1 | 1 | 0 | 0 | 3 |
| 2 | 2 | 1 | 2 | 2 | 3 | 0 |
Так как К155ЛА4 содержит три модуля, элементы X1, X3, X6 помещаем в одну микросхему. Для оставшихся несвязанных элементов будем продолжать компоновку.
Таблица 8
| X8 | X9 | X10 | X12 | X13 | X15 | ||
| X8 | 0 | 1 | 1 | 1 | 1 | 0 | 4 |
| X9 | 1 | 0 | 1 | 1 | 0 | 1 | 4 |
| X10 | 1 | 1 | 0 | 0 | 0 | 1 | 3 |
| X12 | 1 | 1 | 0 | 0 | 1 | 1 | 4 |
| X13 | 1 | 0 | 0 | 1 | 0 | 0 | 2 |
| X15 | 0 | 1 | 1 | 1 | 0 | 0 | 3 |
За базовую принимаем вершину X8, т.к. она имеет максимальное значение, равное 4, и минимальный порядковый номер. Она связана с вершинами X9, X10, X12, X13. Посчитаем для этих вершин функционалы:
L(X9)=4-1=3, L(X10)=3-1=2, L(X12)=4-1=3, L(X13)=2-1=1, L(X15)=3-0=3.
Стягиваем вершину X10, X13 с базовой в четвёртый корпус, т.к. они имеют минимальный функционал.
Таблица 9
| X9 | X12 | X15 | ||
| X9 | 0 | 1 | 1 | 2 |
| X12 | 1 | 0 | 1 | 2 |
| X15 | 1 | 1 | 0 | 1 |
| 2 | 2 | 1 | 0 |
Так как К155ЛА4 содержит три модуля, элементы X8, X10, X13 помещаем в одну микросхему.
Аналогично стягиванием оставшиеся вершины X9, X12, X15 в пятый корпус и помещаем в микросхему.
Выбираем микросхему К155ТВ1. В ней содержится только один модуль, поэтому процесс компоновки проводить не будем, а поместим каждый элемент первого блока в отдельную микросхему.
1.3.2 Компоновка второго блокаВторой блок состоит из пяти логических элементов 2И-НЕ, которые не связаны между собой. Поэтому четыре из них стягиваются в один корпус микросхемы К155ЛА3, а пятый в другой, т.к. микросхема К155ЛА3 содержит только 4 логических элемента.
1.3.3 Компоновка третьего блокаТретий блок состоит из одного JK-триггера, поэтому помещаем его в корпус микросхемы К155ТВ1, содержащей только один элемент.
В результате проведения процесса последовательной компоновки конструктивных узлов РЭА, получили схему электрическую принципиальную состоящую из пяти микросхем D2, D3, D4, D5, D6 типа К155ЛА4, двух микросхем D7, D8 типа К155ЛА3 и одной микросхемы D1 типа К155ТВ1. Схема электрическая принципиальная приведена в приложении 1. Перечень элементов к этой схеме в приложении 2.
По этой схеме построим граф (рис. 4).
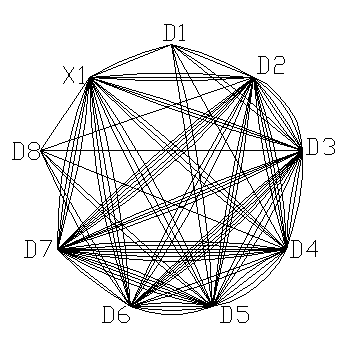
Рис.4
2. Размещение элементов 2.1 Краткое описание алгоритма последовательной установки элементов РЭА
Алгоритм последовательной установки РЭА не требует первоначального размещения элементов. Сущность этого этапа состоит в последовательном закреплении элементов РЭА на монтажной плате относительно каких-либо ранее закрепленных элементов. При этом из числа не размещенных элементов выбирается тот элемент, для которого характеристика, связанная с длиной связи относительно ранее размещенных элементов, оказывается наилучшей. В качестве первоначально закрепленных на монтажной плоскости конструктивных элементов обычно выбирают разъемы. В связи с этим на монтажной плате первыми размещаются элементы, имеющие максимальное количество связей с разъемами.
Вся площадь платы разбивается координатной сеткой на отдельные ячейки, линейные размеры которых больше или равны установочным размерам элементов. Вершины графа, соответствующие разъему, отображаются на подмножество мест, расположенных на одном из краев монтажной платы. Очередная вершина выбирается по максимальному количеству связей с уже размещенными вершинами и помещаются в свободную соседнюю позицию или в такую позицию из числа свободных, которая обеспечивает минимальную длину связей между размещаемой вершиной и уже размещенными вершинами графа.
В качестве исходных данных необходимо ввести данные о модели монтажной платы, ограничения на расположения элементов, на расположение разъема, а так же данные о связях между размещенными элементами.
В качестве критерия выбора очередного элемента, подлежащего установке на плате, используется коэффициент относительной взвешенности связности:
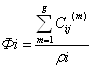 , (10)
, (10)
где ![]() –количество связей i-ого элемента с установленным ранее на
–количество связей i-ого элемента с установленным ранее на
плате j-ым элементом, порядковый номер которого-m;
g – количество уже закрепленных на плате элементов;
![]()
![]() – общее число связей i-ого элемента со всеми остальными
– общее число связей i-ого элемента со всеми остальными
элементами множества X.
2.1.1 Последовательность работы алгоритмаФормируется массив номеров элементов и подготавливается (обнуляется) массив установочных мест.
Выбираем за исходное размещение местонахождение разъема и элементов, закрепляемых на установочных местах платы по требованию разработчика.
Во множестве размещаемых элементов, обнуляем элементы размещенные по требованию разработчика.
Выбираем из множества N ещё не размещенный элемент ![]() для которого значение Фi максимально. Если ряд элементов имеет одинаковое значение Фi, то выбираем элемент с минимальным порядковым номером.
для которого значение Фi максимально. Если ряд элементов имеет одинаковое значение Фi, то выбираем элемент с минимальным порядковым номером.
Для множества незанятых позиций ряда определяем позицию, закрепление которой элемента Ni приводит к минимальному приращению функции цели
![]() , (11)
, (11)
где dij – элемент матрицы расстояний.
Общее суммарное расстояние от закрепляемого элемента к закрепленным будет минимальным. Проверяем, не является ли данная позиция областью, запрещенной для размещения элементов.
Производим закрепление элемента Ni за свободной позицией ряда, в которой обеспечивается минимальное приращение функции цели.
Проверяем все ли элементы размещены на плате, если нет, то процесс повторяется заново.
2.2 Выполнение размещенияПо графу (рис.4) строим матрицу смежности и определяем степень каждой вершины
Таблица 10
| D1 | D2 | D3 | D4 | D5 | D6 | D7 | D8 | X1 |
| |
| D1 | 0 | 2 | 2 | 1 | 2 | 0 | 0 | 0 | 2 | 9 |
| D2 | 2 | 0 | 5 | 4 | 3 | 3 | 6 | 1 | 3 | 27 |
| D3 | 2 | 5 | 0 | 3 | 3 | 6 | 4 | 1 | 3 | 27 |
| D4 | 1 | 4 | 3 | 0 | 4 | 2 | 6 | 1 | 3 | 24 |
| D5 | 2 | 3 | 3 | 4 | 0 | 4 | 5 | 2 | 3 | 26 |
| D6 | 0 | 3 | 6 | 2 | 4 | 0 | 2 | 2 | 4 | 23 |
| D7 | 0 | 6 | 4 | 6 | 5 | 2 | 0 | 0 | 4 | 27 |
| D8 | 0 | 1 | 1 | 1 | 2 | 2 | 0 | 0 | 1 | 8 |
| X1 | 2 | 3 | 3 | 3 | 3 | 4 | 4 | 1 | 0 | 23 |
Составляем модель монтажной платы
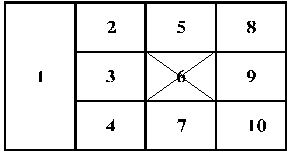 |
Рис. 5 Модель монтажной платы
Затем по модели монтажной платы составляем матрицу расстояний
Таблица 11
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 1 | 0 | 1 | 1 | 1 | 2 | 2 | 2 | 3 | 4 | 3 |
| 2 | 1 | 0 | 1 | 2 | 1 | 2 | 3 | 2 | 3 | 4 |
| 3 | 1 | 1 | 0 | 1 | 2 | 1 | 2 | 3 | 4 | 3 |
| 4 | 1 | 2 | 1 | 0 | 3 | 2 | 1 | 4 | 3 | 2 |
| 5 | 2 | 1 | 2 | 3 | 0 | 1 | 4 | 1 | 2 | 3 |
| 6 | 2 | 2 | 1 | 2 | 1 | 0 | 1 | 2 | 1 | 2 |
| 7 | 2 | 3 | 2 | 1 | 4 | 1 | 0 | 3 | 2 | 1 |
| 8 | 3 | 2 | 3 | 4 | 1 | 2 | 3 | 0 | 1 | 2 |
| 9 | 4 | 3 | 4 | 3 | 2 | 1 | 2 | 1 | 0 | 1 |
| 10 | 3 | 4 | 3 | 2 | 3 | 2 | 1 | 2 | 1 | 0 |
2.2.1 В качестве первого размещенного элемента принимаем разьем X1 (позиция 1). Рассчитываем коэффициенты относительной взвешенной связности по формуле (10)
ФD1= 2/9 = 0,222, ФD2= 3/27 = 0,111, ФD3= 3/27 = 0,111, ФD4= 3/24 = 0,125,
ФD5= 3/26 = 0,115, ФD6= 4/23 = 0,174, ФD7= 4/27 = 0,148, ФD8= 1/8 = 0,125.
На данном этапе будем размещать элемент с максимальным значением ![]() , т.е. элемент DD1.
, т.е. элемент DD1.
Рассчитываем приращение функции цели для незанятых ячеек печатной платы по формуле (11)
F2 = 2*1 = 2, F3 = 2*1 = 2, F4 = 2*1 = 2, F5 = 2*2 = 4,
F6 = 2*2 = 4, F7 = 2*2 = 4,F8 = 2*3 = 6,F9 = 2*4 = 8,F10 = 2*3 = 6.
Выбираем минимальное значение из ![]() . Это соответствует 2,3 и 4 позициям. Выбираем позицию с минимальным номером, т.е. вторую.
. Это соответствует 2,3 и 4 позициям. Выбираем позицию с минимальным номером, т.е. вторую.
2.2.2 В качестве размещенных элементов принимаем разьем X1 (позиция 1) и DD1 (позиция 2). Рассчитываем коэффициенты относительной взвешенной связности по формуле (10)
ФD2= (2+3)/27 = 0,185, ФD3= (2+3)/27 = 0,185,
ФD4= (1+3)/24 = 0,167, ФD5= (2+3)/26 = 0,192, ФD6= (0+4)/23 = 0,174,
ФD7= (0+4)/27 = 0,148, ФD8= (0+1)/8 = 0,125.
На данном этапе будем размещать элемент с максимальным значением ![]() , т.е. элемент DD5.
, т.е. элемент DD5.
Рассчитываем приращение функции цели для незанятых ячеек печатной платы по формуле (11)
F3 = 3*1+2*1 = 5,
F4 = 3*1+2*2 = 7, F5 = 3*2+2*1 = 8, F6 = 3*2+2*2 = 10,
F7 = 3*2+2*3 = 12,F8 = 3*3+2*2 = 13, F9 = 3*4+2*3 = 18,
F10 = 3*3+2*4 = 17.
Выбираем минимальное значение из ![]() . Это соответствует позиции 3.
. Это соответствует позиции 3.
2.2.3 В качестве размещенных элементов принимаем разьем X1 (позиция 1), DD1 (позиция 2) и DD5 (позиция 3). Рассчитываем коэффициенты относительной взвешенной связности по формуле (10)
ФD2= (2+3+3)/27 = 0,296, ФD3= (2+3+3)/27 = 0,296,
ФD4= (1+4+3)/24 = 0,333, ФD6= (0+4+4)/23 = 0,348,
ФD7= (0+4+5)/27 = 0,333, ФD8= (0+1+2)/8 = 0,375.
На данном этапе будем размещать элемент с максимальным значением ![]() , т.е. элемент DD8.
, т.е. элемент DD8.
Рассчитываем приращение функции цели для незанятых ячеек печатной платы по формуле (11)
F4 = 1*1+0*2+2*1 = 3, F5 = 1*2+0*1+2*2 = 6, F6 = 1*2+0*2+2*1 = 4,
F7 = 1*2+0*3+2*2 = 6,F8 = 1*3+0*2+2*3 = 9, F9 = 1*4+0*3+2*4 = 12,
F10 = 1*3+0*4+2*3 = 9.
Выбираем минимальное значение из ![]() . Это соответствует позиции 4.
. Это соответствует позиции 4.
2.2.4 В качестве размещенных элементов принимаем разьем X1 (позиция 1), DD1 (позиция 2), DD5 (позиция 3), DD8 (позиция 4). Рассчитываем коэффициенты относительной взвешенной связности по формуле (10)
ФD2= (2+3+1+3)/27 = 0,333, ФD3= (2+3+1+3)/27 = 0,333,
ФD4= (1+4+1+3)/24 = 0,375, ФD6= (0+4+2+4)/23 = 0,435,
ФD7= (4+5)/27 = 0,333.
На данном этапе будем размещать элемент с максимальным значением ![]() , т.е. элемент DD6.
, т.е. элемент DD6.
Рассчитываем приращение функции цели для незанятых ячеек печатной платы по формуле (11)
F5 = 4*2+0*1+4*2+2*3 = 22, F6 = 4*2+0*2+4*1+2*2 = 16,
F7 = 4*2+0*3+4*2+2*1 = 18,F8 = 4*3+0*2+4*3+2*4 = 32,
F9 = 4*4+0*3+4*4+2*3 = 38, F10 = 4*3+0*4+4*3+2*2 = 28.
Выбираем минимальное значение из ![]() . Это соответствует 6 и 7 позициям. Но позиция 6 запрещенная, поэтому выбираем позицию 7.
. Это соответствует 6 и 7 позициям. Но позиция 6 запрещенная, поэтому выбираем позицию 7.
Похожие работы
... Подставив значения, получим: . Таким образом, можно сказать, что спроектированное устройство на 44% защищено от вибрационных воздействий. 3.1 Разработка принципиальных схем синтезатора Цифровой синтезатор частотно – модулированных сигналов позволяет формировать л.ч.м. – сигналы и предназначен для работы в составе л.ч.м. – ионозонда в качестве возбудителя передатчика. На принципиальной ...
... т. д. Первый метод применяется в основном для изготовления односторонних печатных плат, комбинированные методы — для двухсторонних, а последние — для многослойных печатных плат. Проанализировав электрическую принципиальную схему автоматического телеграфного ключа, приходим к выводу, что наиболее рациональным будет применить односторонний печатный монтаж с без металлизации сквозных отверстий. В ...
... . Подставляя значение Н в (8.6), получим м. Округляем значение до L = 0,135 м. Полученные значения размеров ЛП соответствуют размерам корпуса блока управления электромеханическим замком, полученным в результате компоновочного расчета 9 Мероприятия по защите от коррозии, влаги, электрического удара, электромагнитных полей и ...
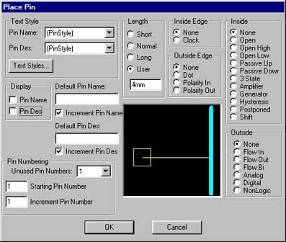
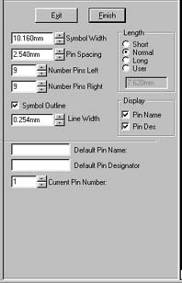
... - Text Style (Текстовый стиль). В этом диалоговом окне установки такие же, как в программе Symbol Editor. 4 РАЗРАБОТАТЬ КОНТАКТНЫЕ ПЛОЩАДКИ Во всех системах автоматизированного проектирования печатных плат информация о графике контактных площадок содержится отдельно от графики корпуса компонента. Это связано с тем, что при изготовлении фотошаблона требуется обеспечить сопряжение программных ...


0 комментариев