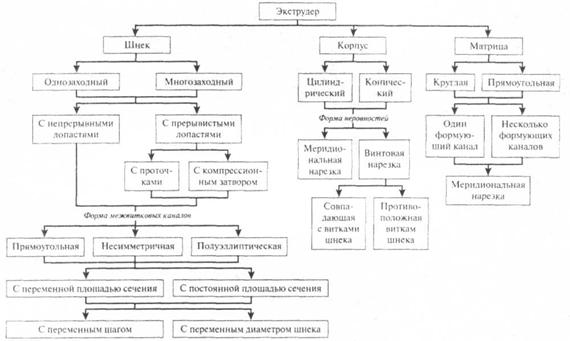
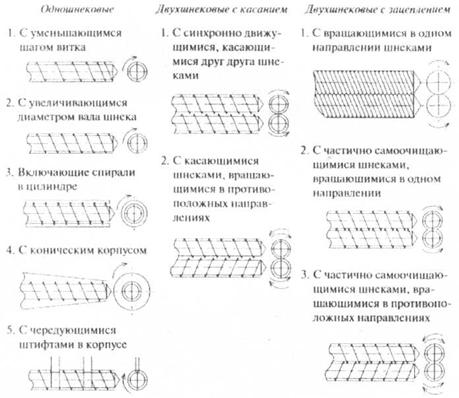
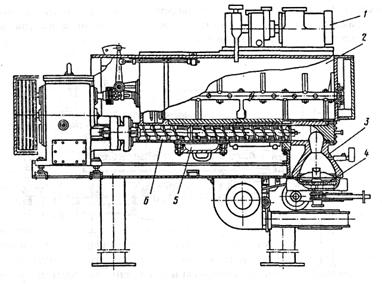
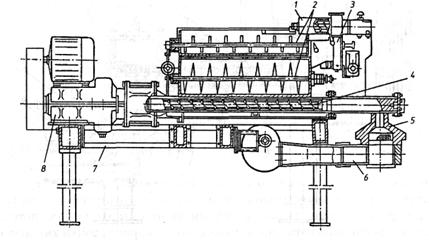
Навигация
Решетчатые фильтры для стационарных случайных процессов
Решетчатые фильтры для стационарных случайных процессов
1. Достоинства решетчатых фильтров
Построение АР модели или синтез АР фильтра требуют вычисления коэффициентов АР. Для этого необходимо обращать корреляционную матрицу, а эта операция, как правило, сопряжена с большим объемом вычислений.
Поиски эффективных алгоритмов вычисления коэффициентов АР привели к синтезу решетчатых структур. Решетчатые структуры могут быть реализованы в виде решетчатых фильтров (РФ). Параметрами РФ являются коэффициенты отражения и число звеньев фильтра. Коэффициенты отражения однозначно связаны нелинейными соотношениями с параметрами АР и определяются, в конечном счете, корреляционной функцией случайного процесса. Число звеньев РФ равно порядку АР модели. РФ, также как и АР фильтры, являются фильтрами предсказания, минимизирующими дисперсию ошибки предсказания.
Несмотря на то, что АР фильтры и РФ математически эквивалентны, между ними существует ряд различий, существенных с практической точки зрения. При цифровой реализации фильтров особое значение играет шум округления. Его появление связано с тем, что значения величин приходится представлять конечным числом разрядов. Как показывает опыт, в этом отношении РФ более эффективны. Объясняется это тем, что ошибки округления (i-1) – го звена в РФ частично компенсируются в i-м звене РФ, чего нет в АР фильтрах.
Другим существенным свойством цифровых фильтров является их чувствительность к квантованной форме представления параметров фильтра. Поэтому, естественно, возникает вопрос: насколько сильно зависят характеристики фильтра от отклонения величин параметров? Доказано, что РФ менее чувствительны к погрешностям квантования параметров по сравнению с фильтрами прямой реализации.
При синтезе РФ, состоящего из p звеньев, используются те же коэффициенты отражения, что и у (p-1) – звенного фильтра. В АР фильтре при увеличении числа звеньев фильтра приходится заново пересчитывать все коэффициенты АР фильтра. Следовательно, использование РФ для обработки случайных сигналов имеет ряд преимуществ, по сравнению с АР фильтрами.
2. Синтез решетчатого фильтра
Несмотря на близость РФ и АР фильтров, использование РФ требует введения новых понятий и соотношений, на основе которых выводится структура РФ. Прежде всего, необходимо остановиться на выводе рекуррентных соотношений, которые носят название алгоритма Левинсона-Дарбина. Алгоритм позволяет вычислять для р-го порядка коэффициенты АР и отражения РФ по найденным коэффициентам АР модели сигнала 1…р порядков.
По аналогии с фильтром прямого предсказания для сигнала, описываемого моделью АР р-го порядка, можно ввести фильтр обратного предсказания, описываемый выражением
![]() , (1)
, (1)
где![]() – коэффициенты фильтра обратного предсказания, состоящего из р звеньев,
– коэффициенты фильтра обратного предсказания, состоящего из р звеньев, ![]() – ошибка обратного предсказания на выходе р-го звена фильтра. Уравнение описывает регрессию значения случайного процесса
– ошибка обратного предсказания на выходе р-го звена фильтра. Уравнение описывает регрессию значения случайного процесса ![]() на последующие
на последующие ![]() .
.
Значения коэффициентов фильтра обратного предсказания находятся с помощью системы уравнений, аналогичной системе уравнений Юла-Уокера можно представить обобщенные уравнения Юла-Уокера в матричном виде
![]() , (2)
, (2)
где ![]() -квадрат СКО, равный дисперсии ошибки прямого предсказания, Rp – корреляционная матрица (p+1) – го порядка
-квадрат СКО, равный дисперсии ошибки прямого предсказания, Rp – корреляционная матрица (p+1) – го порядка
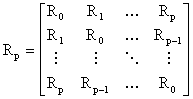 . (3)
. (3)
Чтобы не выходить за рамки общепринятых в теории решетчатых фильтров обозначений, в дальнейшем изложении будет использоваться замена ![]() и
и ![]() .
.
Умножив левую и правую части уравнения на![]() ,
, ![]() и усреднив, легко получить уравнение Юла-Уокера для фильтра обратного предсказания, аналогичное (3)
и усреднив, легко получить уравнение Юла-Уокера для фильтра обратного предсказания, аналогичное (3)
![]() , (4)
, (4)
где![]() – дисперсия ошибки обратного предсказания на выходе p-го звена фильтра обратного предсказания. Объединив матричные уравнения (2) и (4) можно записать общее уравнение
– дисперсия ошибки обратного предсказания на выходе p-го звена фильтра обратного предсказания. Объединив матричные уравнения (2) и (4) можно записать общее уравнение
 . (5)
. (5)
Очевидно, что для (р+1) – звенного фильтра должно так же выполняться соотношение типа
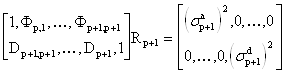 . (6)
. (6)
От матричного уравнения (5) можно перейти к матричному уравнению (6) лишь в том случае, если коэффициенты фильтров прямого и обратного предсказания p-го порядка связаны с коэффициентами фильтра (p+1) – го порядка следующим образом
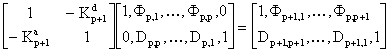 , (7)
, (7)
где![]() - некоторые, так называемые, коэффициенты отражения. Умножив справа левую и правую части матричного уравнения (7), на корреляционную матрицу
- некоторые, так называемые, коэффициенты отражения. Умножив справа левую и правую части матричного уравнения (7), на корреляционную матрицу ![]() можно показать, что коэффициенты отражения удовлетворяют соотношениям
можно показать, что коэффициенты отражения удовлетворяют соотношениям
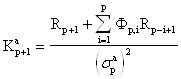 , (8а)
, (8а)
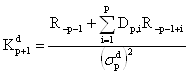 . (8б)
. (8б)
Величины, входящие в соотношения (8а) и (8б), описываемые выражениями
![]() , (9а)
, (9а)
![]() , (9б)
, (9б)
как будет показано ниже, интерпретируются как взаимная корреляция ошибок прямого и обратного предсказания при единичной задержке. Для скалярного случая справедливы равенства
![]() . (10)
. (10)
Используя соотношения (8а), (8б) и учитывая (7), алгоритм Левинсона-Дарбина, позволяющий вычислять коэффициенты АР по коэффициентам отражения, можно представить в виде
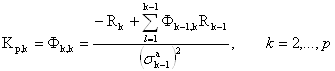 (11)
(11)
![]() , (12)
, (12)
![]() , (13)
, (13)
с инициацией
![]() ,
, ![]() . (14)
. (14)
Найденный алгоритм Левинсона-Дарбина позволяет получить структуру РФ. Формулы дают выражение
![]() , (15)
, (15)
которое с помощью (4) и учетом (15) для р-го звена приводится к виду
![]() . (16)
. (16)
Аналогично можно найти выражение для ошибки обратного предсказания в р звене
![]() . (17)
. (17)
Полученные выражения (16) и (17) дают возможность представить структуру РФ в виде, изображенном на рисунке 1.
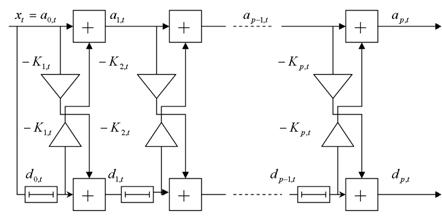
Рисунок 1. Обеляющий РФ
При поступлении сигнала на вход фильтра на выходе каждого звена фильтра появятся ошибки предсказания вперед и назад. Как видно из рисунка 3 ошибки предсказания вперед и назад связаны друг с другом соотношениями (14) и (15).
Можно показать, используя соотношение (17), что решение задачи минимизации дисперсии ошибки предсказания ![]() относительно коэффициента отражения Кp дает следующее выражение для коэффициента отражения
относительно коэффициента отражения Кp дает следующее выражение для коэффициента отражения
![]() . (18)
. (18)
К этому же соотношению можно придти путем несложных преобразований выражений (14) и (15). Таким образом, РФ, коэффициенты отражения которого определяются алгоритмом Левинсона-Дарбина, минимизирует дисперсию ошибки предсказания. Выражение (18) дает удобную оценку коэффициентов отражения РФ, позволяющее обновлять их при адаптации фильтра.
Из рисунка 1 видно, что текущий отсчет случайного процесса можно представить в виде
![]() ,
, ![]() , (19)
, (19)
т.е. взвешенным суммированием ошибок обратного предсказания в предшествующий момент времени с коэффициентами веса, равными коэффициентам отражения. Случайная величина хt, представленная в виде (19), полностью определяется коэффициентами веса, роль которых играют коэффициенты отражения. Таким образом, коэффициенты отражения полностью характеризуют случайный процесс в рамках модели АР. Это свойство коэффициентов отражения РФ позволяет использовать их в качестве информативного признака при распознавании и спектральном оценивании.
Похожие работы
... местные отсосы (предупреждение поступления вредных веществ в помещение путем их отсоса мокрыми пылеулавливающими устройствами); индивидуальной защиты (применение респираторов). Обслуживание оборудования для производства макарон характеризуется концентрацией внимания оператора следящего за выполнением различных процессов. Для снижение зрительных нагрузок применяется боковое естественное освещение ...
... 1 – «-» Причем 1-ый разряд слева – знаковый разряд. 16 14 12 10 8 6 4 2 Т 2Т 2. Связи между аналоговыми и дискретными сигналами. При обработке сигнала на ЭВМ необходимо в максимальной степени, чтобы дискретный или цифровой сигнал содержал все признаки аналогового сигнала. При дискретизации возможна потеря информации, которая ...
... изолировать себя от земли (стоять на сухих досках, деревянной лестнице и т.д.). Билет № 4. ИТР ответственные за безопасную эксплуатацию ТПУ и ТС 1. Требования к персоналу. Обучение и работа с персоналом Лица, принимаемые на работу по обслуживанию теплопотребляющих установок и тепловых сетей, должны пройти предварительный медицинский осмотр и в дальнейшем проходить его периодически в ...
... именно соседние в сигнальном пространстве точки, которые как раз более всего подвержены возможности «перепутаться» под действием помех. 4. Характеристики приема сигналов в телекоммуникационных системах 4.1 Вероятности ошибок различения M известных сигналов Под обнаружением сигнала в радиоэлектронике понимают анализ принятого колебания y(t), завершающийся вынесением решения о наличии или ...
0 комментариев