Розрахунок системи керування

3. Розрахунок системи керування

Напругу Uac обираємо рівною 10В. Для того, щоб струм на вході операційного підсилювача був 10мА обираємо резистори R₁, R₂ по 0,5 кОм кожний. Діоди вибираємо ВА607, що відповідають схемному рішенню. Операційний підсилювач обираємо МС34063.

Розрахунок RC-ланки:

Час імпульсу встановлюємо 10мкс, номінал резистора =5кОм, тоді ємність конденсатора обчислюється:

нФ.

Польовий транзистор VT1 вибираємо IRML2402.

Конденсатор С₂ повинен розрядитись за 0,47 мс струмом джерела струму в 0,1 мА визначається за формулою:

нФ.

Розрахунок резисторів R₄ ,R₅ ,R₆:

Обираємо напругу на резисторі R₄ рівною 1 В, кОмж

Обираємо напругу на резисторі R₆ рівною 1 В, опір R₆ = 1 кОм, тоді R₅= 1 1кОм.

Розрахунок резисторів R₇ ,R₈:

Резистори R₇ ,R₈ повинні забезпечити рівень компорирування на половини напруги живлення, їх номінали однакові, по 10кОм.

Розрахунок підсилювача на біполярному транзисторі VT3:

Біполярний транзистор VT3 вибираємо ВС848.

Резистор

Ом;

кОм.

Розрахунок підсилювача сигналу помилки:

Коефіцієнт підсилення обираємо рівним 20.

R₁₁= 100 кОм, R₁₂ = 20* R₁₁=2 МОм, R₁₃= R₁₁= 100 кОм

Розрахунок формувача опорної напруги:

Напруга на R₁₆:

;

Задаємося В, R₁₆= 5 кОм, тоді R₁₄= 31 кОм, а R₁₅= 0,1R₁₆= 500 Ом,

Ом.

Конденсатор С₃ обираємо 0,22 мкФ.

Діаграми роботи системи керування (для одного вентиля) зображено на рис. 3.1.

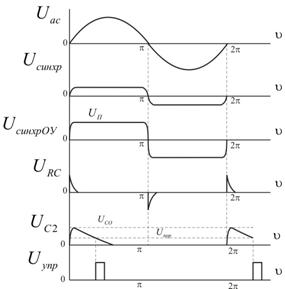
Рис. 3.1.

4. Моделювання перехідного процесу

Для моделювання процесів в схемі, ми маємо скласти диференційні рівняння, що описують роботу схеми. Перед тим як скласти систему рівнянь необхідно зобразити схему заміщення і обумовити спрощення моделей елементів. Всі ветилі мають однакові параметри та однаковий опір у відкритому стані, дросель замінюється індуктивністю та послідовно під’єднаним опором, напруга на всіх обмотках трансформатора однакова, лише зміщена по фазі, враховується опір обмоток, опір конденсатора не враховуємо.

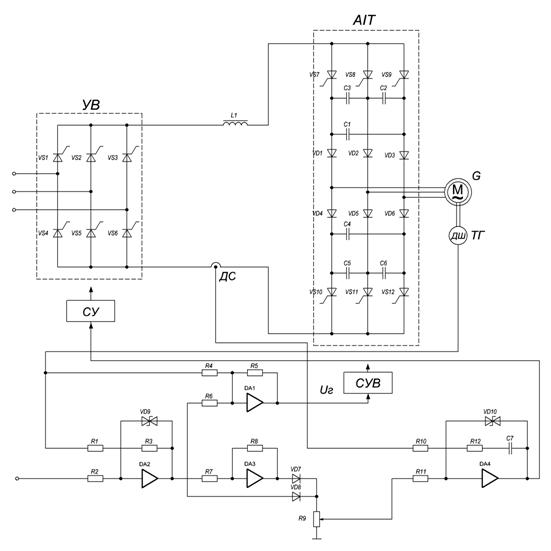
Схема заміщення зображена на рис.4.1.

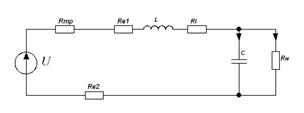
Рис.4.1.

Оскільки форма напруги періодична то достатньо дослідити лише два відрізки часу коли відкритими є два вентильних елемента протягом . Періодом Т будемо вважати сусідні моменти природної комутації. Кут керування обираємо номінальний . Для зручності перейдемо в області часу, кут  замінимо на с и в радіани .

Протягом періоду Т структура схеми заміщення не міняється, змінюється лише напруга U.

Система диференційних рівнянь має наступній вигляд:

;

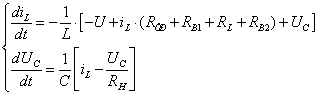В залежності від інтервалу напруга U буде рівною:

, .

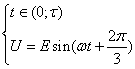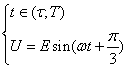Отриману систему рівнянь використаємо при моделюванні перехідних процесів у схемі. Моделювання будемо здійснювати за допомогою програми MathLab 7.5. Блок-схема програми моделювання перехідних процесів у схемі наведено у Додатку №1.

В результаті моделювання були отримані графіки струму індуктивності, напруги на ємності, випрямленої напруги та основних напруг системи керування: ГПН та сигналу помилки.

Графік перехідного процесу показано на рис. 4.2.

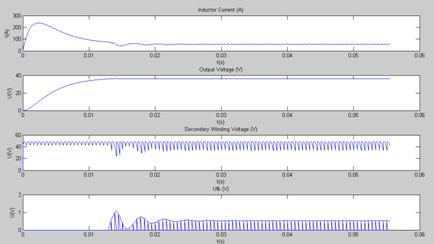
Рис. 4.2.

Більш детально графіки в момент пуску та для усталеного режиму показано на рис. 4.3 та 4.4 відповідно.

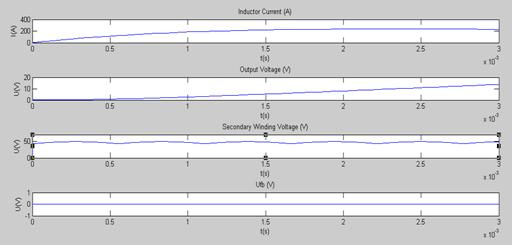
Рис. 4.3.

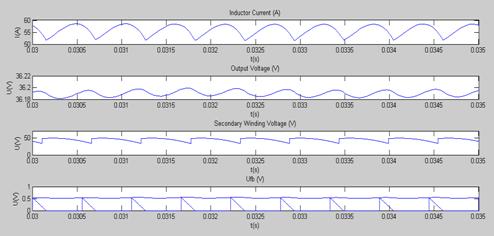
Рис. 4.4.

5. Дослідження стійкості

Дослідження стійкості будь-якої системи можна розбити на етапи:

1.  Складання рівнянь на окремих інтервалах роботи;

2.  Об’єднання отриманих рівнянь;

3.  Лінеаризація рівнянь відносно однієї із змінних стану;

4.  Знаходження розв’язку усталеного режиму;

5.  Дослідження стійкості по характеристичному рівнянню.

Рівняння для кожного інтервалу роботи схеми ми знайшли в попередньому пункті, при досліджені перехідного процесу:

Для зручності написання систем об’єднаємо послідовно підключені опори  Ом.

1. ;

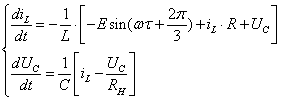2. .

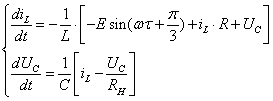Систему керування можна описати наступною системою рівнянь:

,

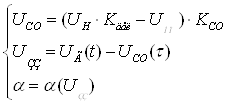де,  - сигнал помилки,  - вихідна напруга,  - опорна напруга,  - сигнал зворотнього зв’язку,  - коефіцієнт підсилення ,  - функція, що приймає значення 1 при високому рівні на виході СК, а 0 – при низькому.

Використаємо  для того, щоб об’єднати системи рівнянь для двох інтервалів роботи схеми.

.

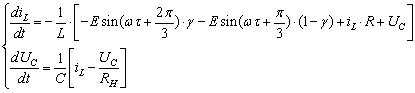Представимо отриману систему рівнянь у матричній формі:

,

де

, ,.

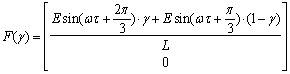Лінеаризуємо отриману систему в "малому". Знайдем диференціали по змінним стану від правої і лівої частин системи. Ввівши позначення , , отримаємо рівняння

,

де ,,.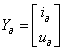

Оскільки матриця  не залежить від змінних стану та , то .

,

,

де  – -функція Дірака.

Використаємо наступну властивість -функції

,  ,

;

.

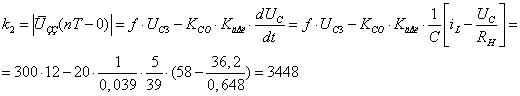оскільки , то можемо записати:

.

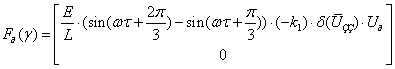Використовуючи властивість -функції , визначимо значення добутку:

.

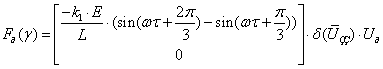Оскільки

 

то ;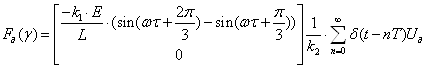

,

де матриця S має вигляд:

.

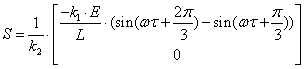Визначимо матриці А₁ та А₂:

, ,.

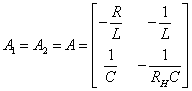Знайдемо розв’язок рівняння на інтервалі постоянства структури з використанням неперервного перетворення Лапласа на інтервалі .

,де .

Застосуємо неперервне перетворення Лапласа до лівої і правої частини рівняня:

.

Рішаючи отримане матричне рівняння отримаємо:

, де  – зворотня матриця;

,.

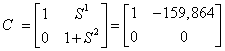Для переходу в часову область використаємо зворотнє перетворення Лапласа, в результаті чого отримаємо:

,

де .

Знайдемо розв’язок рівняння на інтервалі постоянства структури з використанням неперервного перетворення Лапласа на інтервалі :

,де .

Застосуємо неперервне перетворення Лапласа до лівої і правої частини рівняня:

.

Рішаючи отримане матричне рівняння отримаємо:

,

де  – зворотня матриця.

Для переходу в часову область використаємо зворотнє перетворення Лапласа, в результаті чого отримаємо:

;

де .

Підставимо в рівняння для інтервалу  значення часу , а в рівняння для інтервалу  – значення часу , після чого підставимо перше рівння у друге:

;

;

.

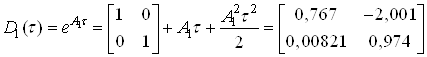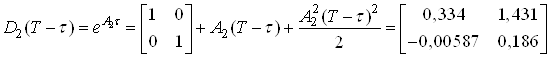Отримане рівняння визначає стійкість у "малому" початкової нелінійної системи в околі установившогося режиму .

Застосуємо дискретне перетворення Лапласа до отриманого рівняння:

,

де  – дискретне зображення Лапласа ;  – початкове значення вектору : . Перетворивши отримане рівняння отримаємо:

.

В результаті відкриття визначника , знаходимо характеристичний многочлен:

;

.

Зробимо заміну змінних ;

;

,.

Корені даного рівняння знаходяться в середині кола одиничного радіуса і тому можна зробити висновок, що дана схема являється стійкою.

6. Висновки

У даній курсовій роботі був виконаний розрахунок перехідного процесу, що виникає при включенні пристрою, і стійкості в "малому" сталому режимі, на прикладі трьохфазного мостового випрямляча із ШІМ першого роду. При виконанні курсової роботи була спроектована принципова схема пристрою. Схему такого випрямляча можна віднести до схем зі постійною структурою й аналізувати неї на інтервалах роботи, де змінюється напруга.. Для розрахунку перехідного процесу були складені диференціальні рівняння й по них побудовані графіки, елементи силової частини при цьому замінялися їхніми ідеалізованими моделями. Також був проведений розрахунок стійкості системи, що показав, що дана система є стійкою.

7. Література

 

1. Г.С. Найвельт и др. "Источники электропитания радиоэлектронной аппаратуры. Справочник". М.: Радио и связь, 1985

2. Перетворювальна техніка. Частина 1: Підручник./ В. С. Руденко, В. Я. Ромашко, В. Г. Морозов. – К.: ІСДО, 1996.– 262 с.

3. Замкнутые системы преобразования электрической энергии. Под ред. Д-ра техн. наук В.Я. Жуйкова. – Киев, "Техника", 1989.

4. Методические указания к курсовой работе по курсу "Преобразовательная техника" для студентов специальности "Промышленная электроника" всех форм обучения. Сост.: В. С. Руденко, В. Г. Морозов, В. Я. Ромашко. – Киев: КПИ, 1984. – 56с.

Додаток 1.

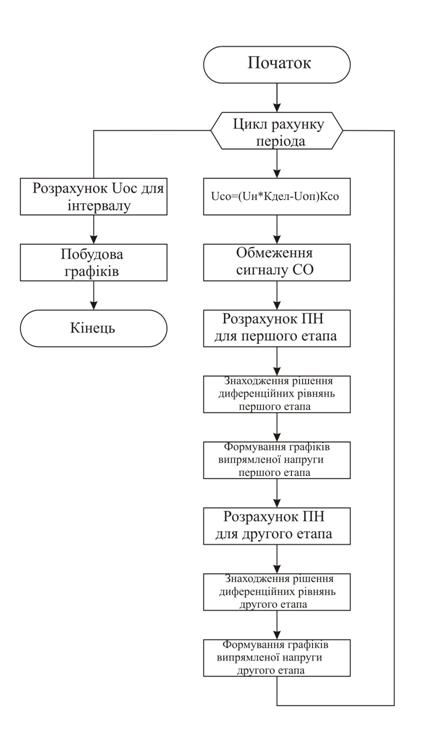
Додаток 2.

function main;

Rv1=37*10^(-3);

Rv2=Rv1;

Rdr=80*10^(-3);

Rd=0.648;

Ld=160*10^(-6);

C=39*10^(-3);

E=20*sqrt(6);

U0=0;

I0=0;

t=0;

K=-3500;

U_start=0;

Kfb=20;

Pi=3.1415;

L=Pi/7;

s=0;

Z=0;

Y=[0, 0];

t=0;

PhaseShift=2*Pi/3;

Ufb=0;

Uref=5;

D=0;

Dx=0;

Dt=0;

Dtx=0;

Ufb=0;

O=0;

P=0;

w=2*Pi*300;

for f=1:100

s=0;

Z=0;

Dtx=0;

Dx=0;

U_start=(Y(end,2)*5/36-Uref)*Kfb;

if (U_start<0)

U_start=0;

end

Dtx(1)=0;

Dtx(2)=-U_start/K;

if (Dtx(2)>((Pi/3)/w))

Dtx(2)=(Pi/3)/w;

end

Dx(1)=U_start;

Dx(2)=K*Dtx(2)+U_start;

Y0=[Y(end,1),Y(end,2)];

[s,Z]=ode113(@F_first, [0 (Dtx(2)+10^-8)], Y0);

s=s+t(length(t));

Y=[Y;Z];

t=[t;s];

n=0;

Ox=0;

Px=0;

for x=0:0.000001:Dtx(2)+10^-8

n=n+1;

Ox(n)=E*sin(w*x+PhaseShift);

Px(n)=x;

end

Px=Px+P(length(P));

P=[P, Px];

O=[O, Ox];

PhaseShift=PhaseShift-Pi/3;

PhaseShift=PhaseShift+(Dtx(2)+10^-8)*w;

Dtx(3)=(Pi/3)/w;

Dx(3)=0;

s=0;

Z=0;

Y0=[Y(end,1),Y(end,2)];

[s,Z]=ode113(@F_first, [0 (Dtx(3)-Dtx(2))+10^-8], Y0);

s=s+t(length(t));

Y=[Y;Z];

t=[t;s];

n=0;

Ox=0;

Px=0;

for x=0:0.000001:(Dtx(3)-Dtx(2))

n=n+1;

Ox(n)=E*sin(w*x+PhaseShift);

Px(n)=x;

end

Px=Px+P(length(P));

P=[P, Px];

O=[O, Ox];

PhaseShift=PhaseShift+(Dtx(3)-Dtx(2))*w;

Dtx=Dtx+Dt(length(Dt));

D=[D, Dx];

Dt=[Dt, Dtx];

end

for x=1:length(t)

Ufb(x)=(Y(x, 2)*5/36-Uref)*Kfb;

if (Ufb(x)<0)

Ufb(x)=0;

end

end

I=Y;

I(:, 2)=[];

subplot(4,1,1);

plot(t,I);

xlabel('t(s)');

ylabel('I(A)');

title('Inductor Current (A)');

hold on;

I=Y;

I(:, 1)=[];

subplot(4,1,2);

plot(t,I);

title('Output Voltage (V)');

xlabel('t(s)');

ylabel('U(V)');

subplot(4,1,3);

plot(P,O);

xlabel('t(s)');

ylabel('U(V)');

title('Secondary Winding Voltage (V)');

subplot(4,1,4);

plot(t,Ufb);

hold on;

plot(Dt, D);

title('Ufb (V)');

xlabel('t(s)');

ylabel('U(V)');

function G = F_first(t, y)

Ud=E*sin(w*t+PhaseShift);

G=[-1/Ld*(-Ud+y(1)*(Rv1+Rv2+Rdr)+y(2)); 1/C*(y(1)-y(2)/Rd)];

end

end