Навигация
0 q x
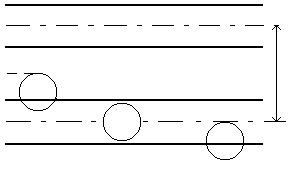
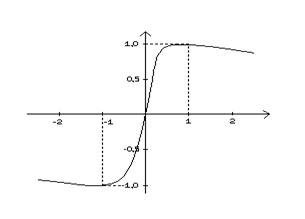
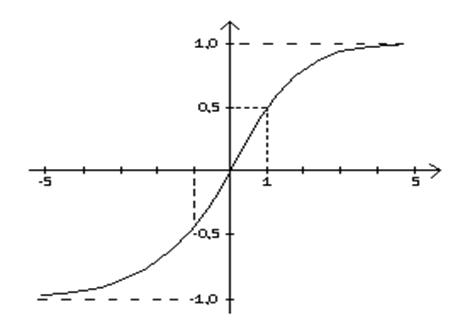
Рис. 2.2. Зависимость ПС от радиального положения пятна.
Для получения двухполярного сигнала ошибки, в котором знак определяет направление смещения, а амплитуда - величину смещения, применяются два дополнительных сканирующих пятна, которые проецируются на диск со смещением λ относительно дорожки в радиальном направлении. Аппроксимируем изменения ПС сигнала UПС функций косинуса в соответствии с равенством:
![]() ,
,
где а – уровень сигнала снимаемого с основного сканирующего пятна;
b – амплитуда переменной составляющей.
Тогда два пятна спутника, детектируемые двумя раздельными фотоприемниками, дадут следующие сигналы:
![]() ;
;
![]() ;
;
Разностный сигнал:
![]() ,
,
является нечетной функцией радиального положения x. Амплитуда и наклон UP(x) максимальны, если ![]() = 1 или
= 1 или ![]() .
.
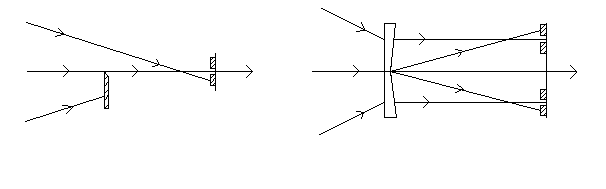
Пятна-спутники получаются с помощью (фазовой) дифракционной решетки, размещенной в диафрагме объектива. Смещение пятен-спутников в радиальном направлении составляет q/4 (см. рис.2.3), а в направлении дорожки гораздо больше (обычно 20 мкм.).
q
l |
Рис.2.3. Расположение пятен - спутников на диске.
Изменением углового положения решетки можно изменять смещение ![]() и тем самым оптимизировать сигнал ошибки радиального слежения UP. Такая схема достаточно проста и очень стабильна.
и тем самым оптимизировать сигнал ошибки радиального слежения UP. Такая схема достаточно проста и очень стабильна.
В методе двух пятен измеряется полная световая мощность пятна плоскости, сопряженной с поверхностью диска. При этом любое изменение интенсивности света в поперечном сечении отраженных лучей не играет роли.
В этом случае сигнал ошибки радиального слежения, как и в методе двух пятен, получается как разность сигналов с двух фотоприемников и определяется выражением
Up(x)=siny10×sin![]() .
.
Уравнение содержит сомножитель siny10, значение которого зависит от средней глубины пит. Питы со средней глубиной, близкой к четверти длины волны лазера и контрастные черно-белые структуры имеют значение y10»p и дают очень малый сигнал. Поэтому при использовании данного метода в процессе изготовления диска-оригинала при формировании глубины пит необходимо уходить из этой запрещенной области. Практически удается получить значения siny10=(0.5¸0.7), что вполне приемлемо для осуществления радиального метода.
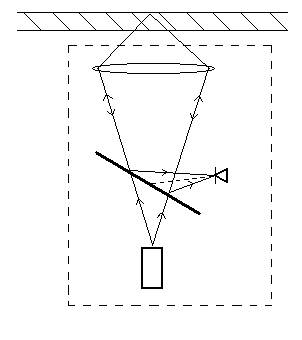
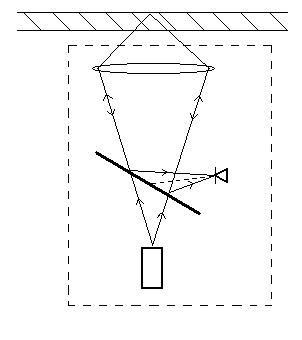
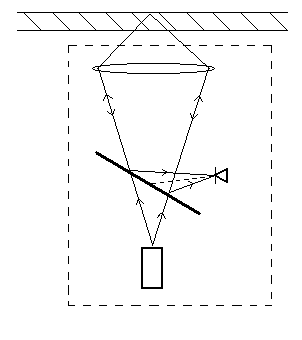
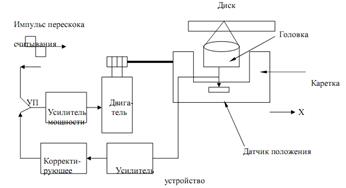
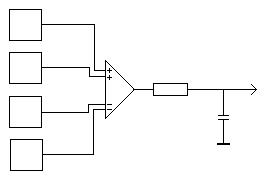
Схема, поясняющая работу датчика положения, показана на рис. 2.4.
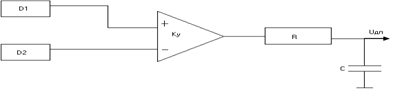
Рис 2.4. Схема датчика положения.
Уравнения имеют вид:
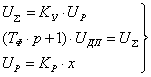
где kp – крутизна характеристики сигнала ошибки радиального слежения, которая определяется линеаризацией характеристики сигнала расфокусировки.
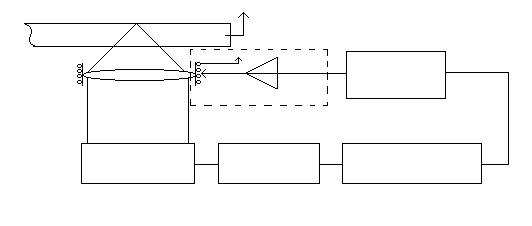
Схема датчика положения приведена на рис 2.5.

Рис. 2.5. Схема датчика положения.
Тогда передаточная функция будет выглядеть так:
![]()
где Ку – коэффициент передачи суммирующего усилителя; ![]()
Тф – постоянная времени фильтра низких частот и находится по формле:
![]()
где λ – максимальное расстояние между двумя переходами от пита к ленду в канальном ходе на дорожке диска.
f – скорость считывания канального хода потока данных.
f=14·F, f=2100 Кбайт/с=1,68·107 бит/с;
Тф=3,05·10-7 с;
Кр – находится путем линеаризации (см. Приложение 1)
![]() ,
,
тогда передаточная функция ![]()
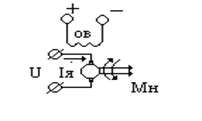
Расчет линейного электродвигателя
Далее сигнал выхода усилителя мощности поступает на исполнительный двигатель, как правило линейный электродвигатель (ЛЭД), работающий по принципу громкоговорителя. Составными частями такого двигателя являются: катушка, постоянный магнит и, возможно, магнитопровод из магнитномягкого железа.
Пригодные к применению конструкции ЛЭД могут быть разделены на две основные группы с подвижной катушкой и с подвижным магнитом.
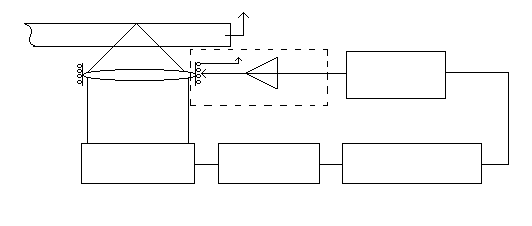
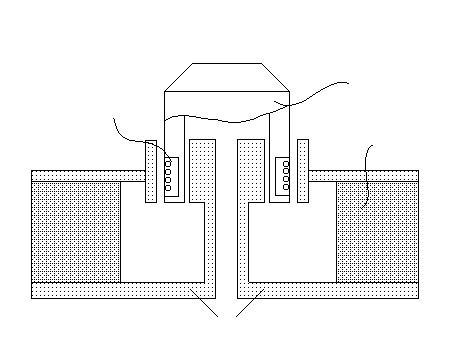 Конструкция с подвижной катушкой (рис.3.1) имеет ряд преимуществ и недостатков. Помимо проблем обрыва проводников, подводящих ток к катушке, движущая часть имеет обычно плохой тепловой контакт с окружающей средой (высокое тепловое сопротивление RT). Тепло, выделяющееся в подвижной катушке, приводит к росту температуры всей подвижной части, в частности объектива, что нежелательно. Это в конечном счете приводит к уменьшению среднего значения силы, развиваемой данным ЛЭД.
Конструкция с подвижной катушкой (рис.3.1) имеет ряд преимуществ и недостатков. Помимо проблем обрыва проводников, подводящих ток к катушке, движущая часть имеет обычно плохой тепловой контакт с окружающей средой (высокое тепловое сопротивление RT). Тепло, выделяющееся в подвижной катушке, приводит к росту температуры всей подвижной части, в частности объектива, что нежелательно. Это в конечном счете приводит к уменьшению среднего значения силы, развиваемой данным ЛЭД.
считывающая
головка
катушка
магнит
магнитопровод
Рис.3.1. Привод головки с подвижной катушкой.
Достоинством системы с подвижной катушкой является то, что стационарная магнитная система может быть увеличена и, следовательно, с ее помощью можно обеспечить более сильное магнитное поле (высокое значение магнитной индукции В).
Альтернативным решением может быть конструкция с подвижным постоянным магнитом и неподвижной катушкой. В этом случае отвод тепла от катушки не является серьезной проблемой (низкое RT) и максимально допустимая температура катушки Ткат maxможет быть выше, так как она изолирована от объектива. Но развиваемая ЛЭД сила будет меньше из-за ослабления магнитного поля (низкое В), поскольку объем магнита меньше. Увеличение же магнита нежелательно, так как приводит к возрастанию массы подвижной части, что ухудшает динамические свойства САРФ.
Поэтому в реальных конструкциях применяется ЛЭД с подвижной катушкой.
Поскольку оба типа ЛЭД являются одинаковыми по принципу действия и различаются лишь подвижностью составляющих их частей, уравнения, описывающие их поведение можно представить в виде:
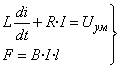 ,
,
где: L – индуктивность катушки;
R=Rк+Rум - сопротивление катушки и внутреннее сопротивление усилителя мощности;
I - ток катушки;
В – магнитная индукция;
l – длина проводника катушки в магнитном поле;
F – сила действующая на катушку;
UУМ – напряжение на выходе усилителя мощности,
или в операторной форме:
(Т·Р+1) F=LлэдUум; (2)
где ![]() - постоянная времени ЛЭД;
- постоянная времени ЛЭД;
![]() - коэффициент передачи ЛЭД;
- коэффициент передачи ЛЭД;
l = π dk W;
W – число витков катушки ЛЭД.
Переходя к изображению, получим передаточную функцию:
![]() ;
;
![]() ;
;
![]() ;
;
Клэд=2,355;
![]()
![]()
Расчет оптической системы
Основная цель, стоящая при разработке подвески, обеспечить движение головки только по жестко заданным направлениям. Подвески могут быть с помощью линейных подшипников механического или электромагнитного типа и пружинных гибких направляющих. В первом случае перемещение в направлении регулирования ничем не ограничивается, а в перпендикулярных направлениях предотвращается путем выбора соответствующих подшипников с минимально возможными допусками у механических и максимальной жесткостью у электромагнитных. Тогда с учетом демпфирования в подвесе и диссипации энергии в катушке, уравнения движения подвижной части имеют вид:
![]() ,
,
где ![]() - коэффициент вязкого трения,
- коэффициент вязкого трения,
или в операторной форме
![]() ,
,
где ![]()
![]() .
.
![]() , Т1=0,75 с;
, Т1=0,75 с;
![]()
Расчет корректирующего устройства
Для надежной работы устройства, необходимо включить в его схему еще один элемент, обеспечивающий заданное качество переходного процесса. Но перед этим нужно добиться требуемого качества установившегося режима. Система должна обеспечивать точность Xmax=0,2 мкм при входном воздействии gmax=500 мкм, отсюда можно найти суммарный коэффициент усиления всех звеньев системы.
![]()
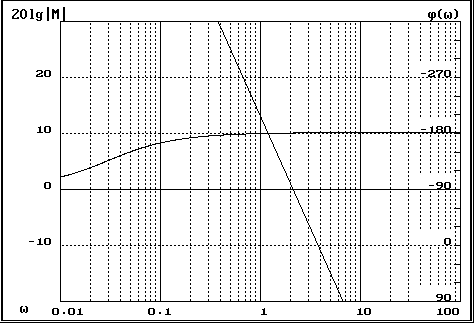
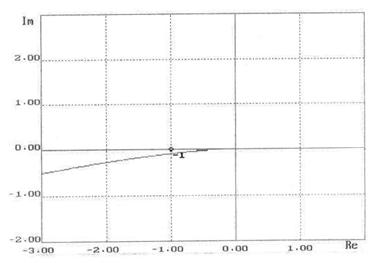
Необходимо построить при помощи программного пакета ТАУ, нескорректированные логарифмические амплитудно-частотные характеристики (ЛАЧХ) и логарифмические фазо-частотные характеристики (ЛФЧХ), определить частоту среза ω0 (см. Приложение 2).
После построения ω0=3000 1/с.
Рекомендуемый наклон скорректированной ЛАЧХ в области частоты среза -20 Дб на декаду. Т.к. одна из постоянных времени лежит ниже частоты среза, то наклон не скорректированный ЛАЧХ в этой области примерно -60 Дб/декаду. Следовательно, чтобы поднять на 40 Дб не скорректированную ЛАЧХ передаточная функция корректирующего устройства должна иметь вид:
![]()
Постоянные времени в данном случае выбираются по соотношению:
![]() ;
;
![]() ;
;
Выбираем τ=0,0006 с,
Т=0,0001 с.
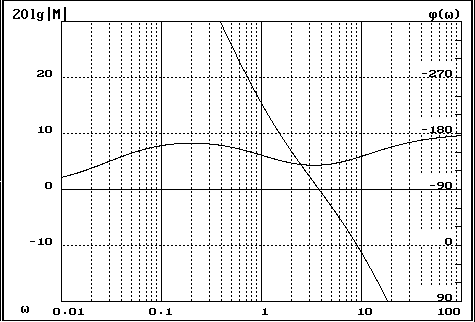
Таким образом мы получили следующую передаточную функцию:
W(s)=Wдп(s)·Wиэ(s)·Wоу(s) ·Wку(s)
![]()
Ввод данных:
![]() , где
, где
К=1; Т1=Т2=0,6; Т3=0,3; Т4=0,2; λ=1; τ=0
![]() , К=2500, Т=750 с
, К=2500, Т=750 с
Заключение
В ходе выполнения данной курсовой работы был проведен синтез системы автоматического регулирования радиального положения пятна. Скорректированная система получилась устойчивой.
Список литературы
1. Сапаров В.Е., Максимов Н.А. Системы стандартов в электросвязи и радиоэлектронике. М.: Радио и связь, 1985. 248 с.
2. Микропроцессорные системы автоматического управления./Под ред. Бесекерского В.А. Л., Машиностроение, 1988.
3. Бесекерский В.А., Изранцев В.В. Системы автоматического управления с микроЭВМ. М., Наука, 1987.
4. Бесекерский В.А., Попов Е.П. Теория систем автоматического регулирования. М., Наука, 1975.
5. Теория автоматического управления./Под ред. Воронова А.А. М., Высшая школа, 1986, Т.1, 2.
6. Основы автоматического регулирования и управления./Под ред. Пономарева В.М., Литвинова А.П. М., Высшая школа, 1974.
7. Сборник задач по теории автоматического регулирования и управления./Под ред. Бесекерского В.А. М., Высшая школа, 1978.
Похожие работы
... управления, одна из которых действует в вертикальном, а другая в горизонтальном, по отношении к диску, направлениях. Называются они соответственно системой автоматического регулирования фокусировки (САРФ) и системой автоматического регулирования радиального положения пятна относительно дорожки записи (САРД). В видео дисковых системах дополнительно используется система управления в тангенциальном ...
... которых действует в вертикальном, а другая в горизонтальном, по отношении к диску, направлениях. Называются они соответственно системой автоматического регулирования фокусировки (САРФ) и системой автоматического регулирования радиального положения пятна относительно дорожки записи (САРД). В видео дисковых системах дополнительно используется система управления в тангенциальном направлении (вдоль ...
... , а именно: –Вращения диска (САРВ); –Тангенциального слежения (САРТ); –Радиального слежения за дорожкой (САРД); –Радиального перемещения каретки (САРРП); – Вертикального слежения за фокусировкой (САРФ). 2. Описание работы САРРП Системы радиального слежения за дорожкой обычно имеют малый диапазон смещения пятна. Для считывающей головки это, как правило, электромеханические ограничения, ...
... вращающегося диска. В настоящее время оптические дисковые системы снабжены пятью системами автоматизированного регулирования, а именно: – Вращения диска (САРВ); – Тангенциального слежения (САРТ); – Радиального слежения за дорожкой (САРД); – Радиального перемещения каретки (САРРП); – Вертикального слежения за фокусировкой (САРФ). 1. Описание работы САР На рис.1. схематически ...
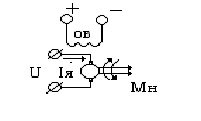


0 комментариев