Методы исследования структурной надежности радиотехнических систем

2. Методы исследования структурной надежности радиотехнических систем 2.1 Точный метод анализа структурной надежности радиотехнических систем

Надежность является одним из основных критериев, которым должны удовлетворять современные сети коммутации. Учесть непосредственно показатели надежности в ходе синтеза сети обычно не удается, поэтому, на этапе синтеза необходимые предпосылки для обеспечения надежности закладываются в косвенном виде, например как топологическое требование обеспечения между некоторыми подмножествами пар узлов не менее заданного числа независимых путей (требование v-связности). Получаемые варианты построения сети затем проверяются на соответствие заданным показателям надежности. Если при выбранном числе независимых путей не удается выполнить заданных требований, то повышают степень связности рассматриваемых в процессе синтеза вариантов структуры будущей сети.

Таким образом, задача построения надежной сети сводится к задаче анализа различных вариантов ее структуры по заданным показателям, которые зависят как от надежности ее элементов, так и от способа их взаимного соединения. Наибольшие трудности при расчете обычно сопряжены с учетом способа взаимного соединения элементов (структуры сети), поэтому в дальнейшем основное внимание мы уделим оценке именно структурной надежности.

Элементами сетей коммутации будем считать направления связи, а также технические средства, входящие в состав, узлов коммутации, концентраторов нагрузки и комплексов сетевого доступа абонентов. При этом основными компонентами, показатели надежности которых проектировщик сети изменить не может, являются каналы связи и процессоры. Связь между смежными узлами сети организуется с помощью последовательно и параллельно включенных каналов, а технические средства на узлах связи состоят из последовательно и параллельно включенных процессоров.

Обратимся сначала к определению показателей надежности компонентов сети. Для определения любого из них прежде всего необходимо сформулировать понятие отказа. Несмотря на кажущуюся очевидность этого понятия в ряде случаев его формулировка весьма затруднительна. Возьмем для примера канал связи. Зачастую качество канала ухудшается постепенно, и установить момент, начиная с которого следует констатировать отказ канала, довольно сложно. Более того, отдельные показатели качества канала (например, вероятность искажений) имеют статистическую природу, и требуется некоторое время наблюдения за каналом, прежде чем с определенной уверенностью можно будет объявить канал неисправным. Предположим только, что всегда можно задать некоторое время прерывания связи, по истечении которого канал признается неисправным. Обычно это время лежит в пределах от единиц до десятков секунд и зависит от назначения сети и выбранной системы ее контроля и управления.

Предположим, что понятие отказа сформулировано.

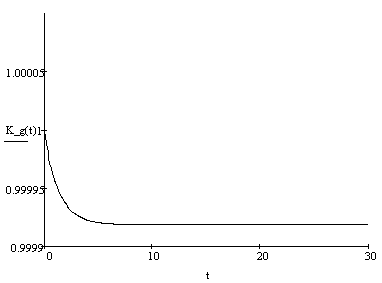
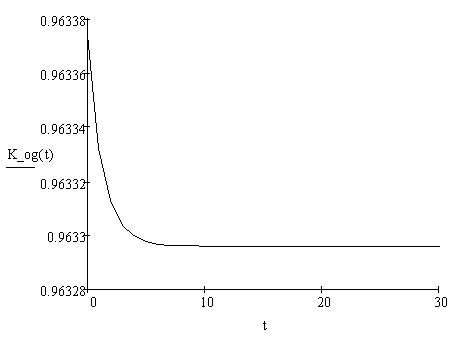
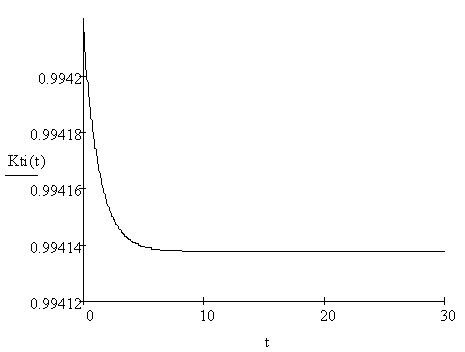
Тогда можно экспериментально определить среднее время пребывания компонента в исправном состоянии Т_и и среднее время его восстановления τ_в. Эти показатели надежности в большой степени зависят от выбранного временя перерыва связи, по истечении которого канал признается неисправным. По этим характеристикам можно определить вероятность того, что компонент находится в исправном состоянии, или его коэффициент готовности

Κ_г=T_и ∕ (T_и+τ_в) (2.1)

и коэффициент простоя

 

K_п=1-K_г=τ_{в ∕} (T_и+ τ_в). (2.2)

Опыт показывает, что коэффициенты готовности и простоя в значительно меньшей степени зависят от критического времени перерыва связи и, кроме того, допускают обобщения на сеть в целом. Поэтому при оценках структурной надежности в качестве исходных данных примем коэффициенты готовности (простоя) компонентов сети.

При последовательном соединении п компонентов сети, например каналов связи, результирующая цепочка будет исправна только в случае исправности всех ее составляющих. Предполагая независимость отказов последовательно соединенных компонентов, результирующий коэффициент готовности K_гр можно представить в виде

K_гр=K_гі, (2.3)

где K_гі - коэффициент. готовности i-ro компонента.

Для повышения надежности направлений связи и технических средств на узлах связи часто используется параллельное включение п каналов или процессоров, при котором результирующий элемент сети будет исправен, если исправен хотя бы один из входящих в него компонентов. Отказ такого составного элемента наступит лишь в случае отказа всех входящих в его состав компонентов, что случится с вероятностью

Κ_пэ=K_пі, (2.4)

где Κ_пэ-коэффициент простоя элемента; K_пі-коэффициент простоя i-го компонента. Если

 

K_пі= K_п, , то Κ_пэ=Кⁿ_п. (2.5)

Формулы (2.4) и (2.5) справедливы лишь в том случае, когда отказы всех рассматриваемых компонентов независимы. Это условие заведомо нарушается, если каналы связи одного направления проходят по одной линии связи или, тем более, находятся в одной системе передачи. Поэтому в дальнейшем будем считать, что все каналы связи каждого направления сети проходят по географически разнесенным линиям связи.

Выражение для результирующего коэффициента простоя элемента Κ_пэ, состоящего из п параллельно включенных идентичных. компонентов, можно получить и другим способом, пользуясь формулой Энгсета. Действительно, совокупность компонентов. можно рассматривать как п конечных источников, причем заявка на обслуживание - это требование ремонта (восстановления). Для определения коэффициента простоя элемента достаточно определить вероятность того, что все п источников будут находиться на обслуживании. Согласно формуле Энгсета эта вероятность

Κ_пэ=С_nⁿAⁿ ∕ C_nⁱAⁱ, (2.6)

где А=τ_в ∕ T_и. Легко установить эквивалентность выражений (2.6) и (2.5). Действительно,

С_nⁿAⁿ ∕ C_nⁱAⁱ= (τ_в ∕ T_и) ⁿ∕ (1-τ_в ∕ T_и) ⁿ= Кⁿ_п

Иногда производительности одного компонента недостаточно для нормальной работы элемента сети, и, чтобы обслужить поступающую нагрузку, необходима одновременная работа, но крайней мере, s компонентов. В этом случае элемент сети (например, направление связи) признается неисправным в случае отказа s+1 и более компонентов. Вероятность этого события можно сразу записать как вероятность того, что одновременно s+1 или более источников (компонентов) потребуют обслуживания (восстановления), исходя из формулы Энгсета

 

Κ_пэ (s) =C_nⁱAⁱ∕ C_nⁱAⁱ (2.7)

Если рассматриваемый элемент сети является узлом коммутации, состоящим из п параллельно включенных процессоров, причем минимально необходимую производительность узла могут обеспечить не менее чем s процессоров, то при отказе (s+l) - ro процессора узел коммутации может выключаться и ресурс оставшихся п-s-1 процессоров расходоваться не будет.д.ля нахождения коэффициента простоя такого элемента можно воспользоваться формулой Энгсета и мнемоническим правилом. Согласно этому правилу можно сразу записать коэффициент простоя интересующего нас элемента

 

Κ_пэ (s+1) = C_n^s+1A^s+1∕ C_nⁱAⁱ (2.8)

Здесь в числителе приводится число ситуаций, благоприятных для отказа элемента, а в знаменателе - общее число ситуаций, соответствующих отказу 0, 1,..., s+1 компонентов. Отказ более чем s+1 компонентов здесь не учитывается, так как по условию в этом случае узел коммутации отключается и ресурс оставшихся компонентов не расходуется. В дальнейшем мы уже не будем интересоваться внутренней структурой элементов сети, полагая, что их показатели надежности p=1 - Κ_пэ определены по одной из приведенных формул.

2.2 Приближенные методы анализа структурной надежности радиотехнических систем

Современные сети коммутации имеют весьма сложную структуру, которая в общем случае не сводится к последовательно-параллельным соединениям, поэтому для расчета надежности таких сетей нельзя применять методы, рассмотренные в §2.1 Прежде всего необходимо сформулировать критерий отказа сети. Через сеть обменивается информацией большое число пар абонентов, причем часто требуется, чтобы вероятность наличия связи между корреспондентами выделенной пары (r, l) была не менее заданной Р_rl. Под наличием связи понимается существование, по крайней мере, одного исправного пути между соответствующими узлами. Конечно, в сложной сети наличие исправного пути еще не гарантирует немедленного установления соединения, так как элементы этого пути могут быть заняты для обмена информацией других корреспондентов. Если, однако, предположить, что термин "наличие связи" относится только к информации высшей категории, доля которой в реальных сетях обычно весьма мала, и элементы любого исправного пути способны обеспечить обмен этой информацией в интересах всех корреспондентов, которые им могут воспользоваться, то возникает возможность рассматривать все пары корреспондентов независимо с точки зрения наличия связи между ними. В элементах сети, производительность которых недостаточна для обслуживания суммарной нагрузки высшей категории, можно предусмотреть согласно (2.7) или (2.8) большее число s рабочих компонентов.

Таким образом, сеть обладает заданной надежностью, если вероятность наличия связи или, как говорят, вероятность связности H_rl для каждой пары узлов не менее заданной Р_rl. В этих условиях расчет структурной надежности сети сводится к расчету вероятности связности между узлами. В дальнейшем рассмотрим и некоторые другие критерии надежности сети.

Итак, задана структура некоторой сети, состоящей из N элементов, причем надежность p_i каждого элемента известна (i=). Необходимо определить вероятность связности относительно выделенной пары узлов r,l. Каждый элемент сети может находиться только в двух состояниях - исправен (И) или неисправен (H). При этом сеть может, очевидно, находиться в любом из S=2^N состояний. В некоторых из этих состояний сеть будет связна (С_rl) относительно рассматриваемых узлов. Если обозначить черезE_s вероятность того, что сеть находится в состоянии s, s=l, S, то искомая вероятность связности сети

H_rl=E_s (2.9)

где E_s=p_i (1-p_i).

При этом по-прежнему предполагается, что отказы всех элементов сети - события независимые.

Рассмотренный метод расчета структурной надежности сети сопряжен с полным перебором ее состояний и при увеличении размеров сети быстро становится нереализуемым даже на современных быстродействующих ЭВМ.

2.2.1 Метод разложения

Несколько менее трудоемким является метод, основанный на разложении структуры сети относительно какого-нибудь ее элемента (метод разложения Шеннона-Мура). Идея этого метода заключается в том, чтобы свести анализируемую структуру к последовательно-параллельным соединениям и тем самым избежать полного перебора состояний. Для примера рассмотрим сеть простейшей структуры в виде мостика (рис.2.1).

Рисунок 2.1 Метод разложения

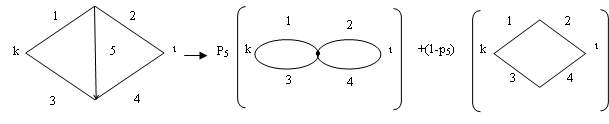
Для простоты положим, что узлы этой сети идеально надежны, а ветви имеют конечную надежность р_i, i=. Нумерация ветвей приведена на рисунке. Проделаем с элементом под номером 5 ("перемычка" мостика) два опыта - "короткого замыкания", соответствующий исправному состоянию элемента, и "холостого хода", соответствующий его неисправному состоянию. Если перемычка находится в исправном состоянии, что случается с вероятностью p₅, то соединяемые ею узлы можно "стянуть" в смысле надежности (см. рис.2.1) и сеть будет иметь вид двух последовательно соединенных и параллельно включенных пар ветвей. Если перемычка находится в неработоспособном состоянии, что случается с вероятностью 1-p₅, то оставшаяся сеть будет иметь вид параллельного соединения цепочек.

Таким образом, мы "разложили" сеть относительно элемента 5, в результате чего получили две подсети с числом элементов на единицу меньше, чем в исходной сети. Поскольку обе подсети представляют собой последовательно-параллельные структуры, то, пользуясь формулами (2.3) и (2.4), можно сразу записать искомое выражение для вероятности связности сети относительно узлов r, l, используя для компактности обозначениеq_i=1-p_i.

 

H_rl=p₅ (1-q₁q₃) (1-q₂q₄) +q₅ [1- (1-q₁q₂) (1-q₃q₄)].

В более сложных структурах может потребоваться неоднократное применение теоремы разложения. Так, на рис.2.2 показано разложение относительно элемента 7 (верхняя строка), а затем по элементу 8 (нижняя строка). Получившиеся четыре подсети имеют последовательно-параллельные структуры и больше не требуют разложений. Легко видеть, что на каждом шаге число элементов в получающихся подсетях уменьшается на единицу а число подсетей, требующих дальнейшего рассмотрения удваивается. Поэтому описанный процесс в любом случае конечен, а число результирующих последовательно-параллельных структур составит 2^m, где т - число элементов, по которым пришлось провести разложение. Трудоемкость этого метода можно оценить величиной 2^m, что меньше трудоемкости полного перебора, но тем не менее все еще неприемлемо для расчета надежности реальных сетей коммутации.

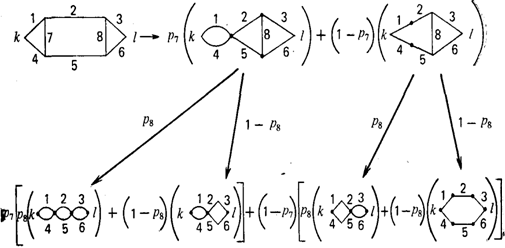
Рисунок.2.2 Последовательное разложение сети

 

2.2.2 Метод сечений или совокупности путей

Рассмотрим еще один метод расчета структурной надежности сетей. Предположим, как и ранее, что необходимо определить вероятность связности сети между заданной парой узлов A,B. Критерием исправной работы сети в данном случае является наличие хотя бы одного пути передачи информации между рассматриваемыми узлами. Предположим, что имеется список возможных путей в виде перечня элементов (узлов и направлений связи), входящих в каждый путь. В общем случае пути будут зависимы, поскольку любой элемент может входить в несколько путей. Надежность R_s любого s-ro пути можно вычислить по формуле последовательного соединения R_s=p_1sp_2s…p_ts, где p_is-надежность i-го элемента s-ro пути.

Искомая надежность H_AB зависит от надежности каждого пути и вариантов их пересечений по общим элементам. Обозначим надежность, которая обеспечивается первыми r путями, через H_r. Добавление очередного (r+1) - го пути с надежностью R_r+1, очевидно, приведет к увеличению структурной надежности, которая теперь будет определяться объединением двух событий: исправен хотя бы один из первых r путей или исправен (r+1) - й путь. Вероятность наступления этого объединенного события с учетом возможной зависимости. отказов (r+1) - го и остальных путей

 

H_r+i=H_r+R_r+i-R_r+1H_{r/ (r+1),} (2.10)

где H_{r/ (r+1) -} вероятность исправности хотя бы одного из первых r путей при условии, что исправен (r+1) - й путь.

Из определения условной вероятности H_{r/ (r+1)} следует, что при ее расчете вероятность исправной работы всех элементов, входящих в (r+1) - й путь, необходимо положить равной единице. Для удобства дальнейших расчетов представим последний член выражения (2.10) в следующем виде:

 

R_r+1H_{r/ (r+1)} = R_r+1¤ H_r (2.11)

где символ (¤) означает, что при перемножении показатели надежности всех элементов, входящих в первые r путей и общих с (r+l) - м путем, заменяются единицей. С учетом (2.11) можно переписать (2.10):

 

∆H_r+1= R_r+1 ¤ Q_r (2.12)

где ∆H_r+1=H_r+1-H_r-приращение структурной надежности при введении (r+1) - го пути; Q_r=1 - H_r вероятность того, что произойдет одновременный отказ первых r путей.

Учитывая, что приращение надежности ∆H_r+1 численно равно уменьшению ненадежности ∆Q_r+1 получаем следующее уравнение в конечных разностях:

 

∆Q_r+1=R_r+1¤ Q_r (2.13)

Легко проверить, что решением уравнения (2.13) является функция

Q_r= (1-R₁) ¤ (1-R₂) ¤…¤ (1-R_r) (2.14)

В случае независимых путей операция символического умножения совпадает с обычным умножением и выражение (2.14) аналогично (2.4) дает коэффициент простоя системы, состоящей из параллельно включенных элементов. В общем случае необходимость учета общих элементов путей заставляет производить умножение согласно (2.14) в алгебраическом виде. При этом число членов в результирующей формуле с умножением на каждый очередной двучлен удваивается и окончательный результат будет иметь 2^r членов, что эквивалентно полному перебору совокупности всех r путей. Например, при r=10 число членов в окончательной формуле превысит 1000, что уже выходит за рамки ручного счета. С дальнейшим увеличением числа путей довольно быстро исчерпываются и возможности современных ЭВМ.

Однако свойства введенной выше операции символического умножения позволяют резко сократить трудоемкость расчетов. Рассмотрим эти свойства более подробно. Согласно операции символического умножения для показателя надежности p_i любого элемента справедливо следующее правило:

 

p_i¤p_i=p_i. (2.15)

Напомним, что второй сомножитель (2.15) имеет смысл вероятности исправной работы i-го элемента при условии его исправности, которая, очевидно, равна единице.

Для сокращения дальнейших выкладок введем следующее обозначение ненадежности i-го элемента:

 

=1-p_i (2.16)

С учетом (2.15) и (2.16) можно записать следующие простые правила преобразования выражений, содержащих р и р:

p_i¤ _i=0

¤ =

p_i¤p_i=p_i (2.17)

¤  =

p_ip_j¤  =p_ip_j-p_ip_s

-p_i=

Для примера использования этих правил при расчете надежности рассмотрим простейшую сеть связи, изображенную на. рис.2.3 Буквы, стоящие у ребер графа, обозначают показатели надежности соответствующих линий связи.

Узлы для простоты будем считать идеально надежными. Предположим, что для связи между узлами А и В можно использовать все пути, состоящие из трех и менее последовательно включенных линий, т.е. следует учесть подмножество путей {μ} = {ab, cdf, cgb, ahf}. Определим приращение надежности, обеспечиваемое каждым последующим путем, по формуле (2.12) с учетом (2.14):

∆Η_r+1=R_r+1¤ (¤₁¤…¤) (2.18),

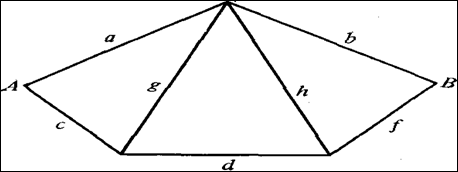
Рисунок.2.3 - Пример сети расчета на ограниченном подмножестве путей

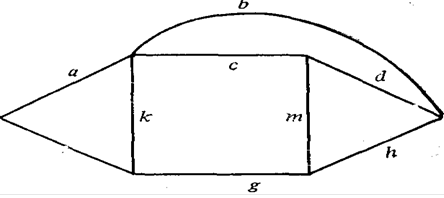
Рисунок 2.4 - Пример сети для расчета надежности по полной совокупности путей, где R_i=1-R₁ аналогично (2.16).

Применяя последовательно формулу (2.18) и правила символического умножения (2.17). к рассматриваемой сети, получаем

∆Η₁=;

∆Η₂=cdf¤ () =cdf*;

∆Η₃=cgb¤ (¤) =cgb**;

∆Η₄=ahf¤ (¤¤) =ahf**.

При расчете последнего приращения мы использовали правило 4, которое можно назвать правилом поглощения длинных цепей короткими; в данном случае его применение дает b¤cgb=b. Если разрешено использование других путей, например пути cdhb, то не представляет труда рассчитать обеспечиваемое им приращение надежности ∆H₅=cdhb¤ (a¤ f¤ g¤ af) = =cdfb*a*f*g. Результирующую надежность сети можно теперь вычислить как сумму приращений, обеспечиваемых каждым из рассмотренных путей:

H_R=∆H_{i (}2.19)

Так, для рассмотренного примера в предположении, что надежность. всех элементов сети одинакова, т.е. a=b=c=d=f=h=g=p, получаем H₅=p²+p³ (1-p²) + +2p³ (1-p) (1-p²) +p⁴ (1-p) ³. При машинной реализации в основу расчета можно также положить формулу (2.13), с учетом того, что

Q_r=∆Q_i (2.20)

Согласно (2.13) имеем следующее рекуррентное соотношение

Q_r+i=Q_r-R_r+1¤Q_r. (2.21)

При начальном условии Q₀=l на каждом последующем шаге из полученного ранее выражения для Q_r следует вычесть произведение надежности очередного (r+1) - го пути на это же выражение, в котором только показатели надежности всех элементов, входящих в (r+1) - й путь, нужно положить равными единице.

В качестве примера рассчитаем надежность сети, изображенной на рис.2.4, относительно узлов А и В, между которыми имеется 11 возможных путей передачи информации. Все расчеты сведены в табл.2.1: перечень элементов, входящих в каждый путь, результат умножения надежности данного пути на значение Q_r, полученное при рассмотрении всех предыдущих путей, и результат упрощения содержимого третьего столбца по правилам (2.17). Окончательная формула для q_AB содержится в последней колонке, если ее читать сверху вниз. В таблице полностью приведены все выкладки, необходимые для расчета структурной надежности рассматриваемой сети.

Таблица 2.1 Результаты расчета надежности сети, изображенной на рис.2.4

Номер пути.	Rr+1	Rr+1Qr	Qr+1
1	ab
2	fgh		-
3	acd	acd*b*	acd* * -
4	frb	frb* *gh	frb* * -
5	argh	argh (*-cd**)	argh** -
6	acmh	acmh (b*-d**-rg* *)	acmh (fg-rg*) -
7	frcd	frcd (**-*gh-b**)	frcd** * -
8	fgmd	fgmd (*-ac**-rb* *-rc***)	fgmdh (-ac*-rb*-rc*) -
9	argmd	argmd [*-c**-h* * - f (-c)]	argmd* * * -
10	frcmh	frcmh (*-ad* *-b* - a* *c-d** *)	frcmh****-
11	fgmcd	fgmcd [*-r**-d* (-r)]	fgmcd*** *

Для уменьшения объема вычислений не следует без необходимости раскрывать скобки; если промежуточный результат допускает упрощения (приведение подобных членов, вынесение за скобку общего множителя и т.д.), их следует выполнить.

Поясним несколько шагов расчета. Поскольку Q₀= 1 (при отсутствии путей сеть разорвана), то для Q₁ из (2.21) Q₁=1-ab=ab. Делаем следующий шаг (6.21) для Q₂=ab-fghab==ab*fgh и т.д.

Рассмотрим подробнее шаг, на котором учитывается вклад пути 9. Произведение показателей надежности составляющих его элементов, записанное во втором столбце табл.2.1, переносится в третий. Далее в квадратных скобках записана вероятность разрыва всех предыдущих восьми путей, накопленная в четвертом столбце (начиная с первой строки), с учетом правила (2.15), согласно которому показатели надежности всех элементов, вошедших в путь 9, заменяются единицами. Вклад четвертой, шестой и седьмой строк оказывается равным нулю по правилу 1. Далее выражение, стоящее в квадратных скобках, упрощается по правилам (2.17) следующим образом: b [fh-cfh-hfc-fhc] =b (fhc-hfc-fhc) =bc (h-fh) =bchf. Аналогично производится расчет относительно всех других путей.

Использование рассматриваемого метода позволяет получить общую формулу структурной надежности, содержащую в рассмотренном случае всего 15 членов вместо максимального числа 2¹¹=2048, получающегося при непосредственном перемножении вероятностей отказов этих путей. При машинной реализации метода удобно представить все элементы сети в позиционном коде строкой бит и использовать встроенные булевы функции для реализации логических элементов преобразований (2.17).

До сих пор мы рассматривали показатели структурной надежности сети относительно выделенной пары узлов. Совокупность таких показателей для всех или некоторого подмножества пар может достаточно полно характеризовать структурную надежность сети в целом. Иногда используется другой, интегральный, критерий структурной надежности. По этому критерию сеть считается исправной, если имеется связь между всеми ее узлами и задается требование на вероятность такого события.

Для расчета структурной надежности по этому критерию достаточно ввести обобщение понятия пути в виде дерева, соединяющего все заданные узлы сети. Тогда сеть будет связана, если существует, по крайней мере, одно связывающее дерево, и расчет сводится к перемножению вероятностей отказа всех рассматриваемых деревьев с учетом наличия общих элементов. Вероятность. Q_s отказа s-го дерева определяется аналогично вероятности отказа пути

Q_s=1-p_is,

где p_is - показатель надежности i-ro элемента, входящего в s-e дерево; n_s число элементов в s-м дереве.

Рассмотрим для примера простейшую сеть в виде треугольника, стороны. которого взвешены показателями надежности а, b, с соответствующих ветвей. Для связности такой сети достаточно существования, по крайней мере, одного из деревьев аb, bс, са. Используя рекуррентное соотношение (2.12), определяем вероятность связности этой сети H. _cb=ab+bca+cab. Если а=b=с=р, получаем следующее значение вероятности связности, которое легко проверить перебором: H. _cb=3р²-2р³.

Для расчета вероятности связности достаточно разветвленных сетей вместо перечня связывающих деревьев, как правило, удобнее пользоваться перечнем сечений {σ} которые приводят к потере связности сети по рассматриваемому критерию. Легко показать, что для сечения справедливы все введенные выше правила символического умножения, только вместо показателей надежности элементов сети в качестве исходных данных следует использовать показатели ненадежности q=1-p. Действительно, если все пути или деревья можно считать включенными "параллельно" с учетом их взаимозависимости, то все сечения включены в этом смысле "последовательно". Обозначим вероятность того, что в некотором сечении s нет ни одного исправного элемента, через π_s. Тогда можно записать

 

π_s=q_1sq_2s…q_ms, (2.22)

где q_{is -} показатель ненадежности i-ro элемента, входящего в s-e сечение.

Вероятность Н_cb связности сети можно тогда представить аналогично (2.14) в символическом виде

 

Н_cb= (1-π₁) ¤ (1-π₂) ¤…¤ (1-π_r) (2.23)

где r - число рассматриваемых сечений. Другими словами, для того чтобы сеть была связна, необходимо, чтобы одновременно были исправны хотя бы по одному элементу в каждом сечении с учетом взаимной зависимости сечений по общим элементам. Формула (2.23) является в некотором смысле двойственной по отношению к формуле (2.14) и получается из последней заменой путей на сечения и вероятностей исправной работы на вероятности пребывания в состоянии отказа. Аналогично двойственным по отношению к формуле (2.21) является рекуррентное соотношение

 

H_r+1=H_r - π_r+1¤ H_r (2.24)

Рассчитаем для примера вероятность связности рассмотренной выше треугольной сети с набором сечений ab, bc, ca. Согласно (2.23) при начальном условии H₀=1 имеем H_cd=ab-bca-cab. При одинаковых показателях ненадежности элементов сети a=b=c=q получаем H_cb=1-q²-2q² (1 - q). Этот результат совпадает с ранее полученным по методу перечисления деревьев.

Метод сечений можно, конечно, применять и для расчета вероятности связности сети относительно выделенной пары узлов, особенно в тех случаях, когда число сечений в рассматриваемой сети значительно меньше числа нулей. Однако наибольший эффект в смысле сокращения трудоемкости вычислений дает одновременное использование обоих методов, которое будет рассмотрено дальше.

 

2.2.3 Метод итераций (двухсторонней оценки)

При проектировании реальных сетей пакетной коммутации обычно отсутствует необходимость точного расчета надежности сети, так как исходные данные по надежности элементов задаются, как правило, с некоторой конечной точностью. Проектировщикам необходимо лишь убедиться в том, что надежность сети, с одной стороны, не ниже заданной и, с другой стороны, не имеет экономически необоснованного запаса. Другими словами, на практике достаточно гарантировать, что истинное значение надежности H₀ находится в некоторых пределах H_min<H₀<H_max.

Можно ожидать, что оценка надежности сети с заданной конечной точностью дозволит сократить трудоемкость расчетов в тем большей мере, чем ниже требуемая точность оценки. Действительно, при расчете надежности по совокупности путей добавление каждого следующего пути приводит к увеличению надежности, а при расчете по совокупности сечений добавление каждого следующего сечения приводит к уменьшению структурной надежности, что создает предпосылки для двусторонней оценки структурной надежности с гарантированной точностью по ограниченным наборам путей и сечений. Рассмотрим эту возможность более подробно.

Обозначим через Q_μ ^(r) результат, полученный при перемножении вероятностей отказов 1-R_s первых r из общего числа n путей. Тогда с учетом следующего (r +1) - го пути получим согласно (2.21) уточненную оценку Q_μ ^(r+1):

Q_μ ^(r+1) = Q_μ ^{(r) -} R_r+1* Q_μ ^{(r) (}2.25)

Функция H_μ ^(r) = l - Q_μ ^(r) является монотонно неубывающей с возрастанием r и при r=n дает точное значение H₀=H_μ ^(n). Промежуточные значения H_μ ⁽ⁿ⁾ при r<n можно рассматривать, как оценки H₀ снизу. Аналогично, исходя из формулы (2.23), можно получить монотонно не возрастающую последовательность H_σ ^(R+1), которую можно рассматривать, как последовательность оценок H₀ сверху. Характер зависимости H_μ ^(r) и H_σ ^(r) от r представлен на рис.2.5 Опыт показывает, что рассматриваемые зависимости при малых r меняются весьма круто, а с дальнейшим увеличением r очень медленно приближаются к общему пределу H₀. Это свойство можно использовать для сокращения трудоемкости оценок надежности с заданной точностью. Действительно, для решения задачи достаточно последовательно просматривать пути μ, пока не выполнится условие H_μ ^(m) ≥H_min и затем просматривать сечения σ, пока не выполнится условие H_σ ^(r) ≤H_min. Если для некоторого m окажется, что H_μ ^(m) >H_max, то можно прекратить расчеты и принять решение, что в сети заложена излишняя избыточность, а если для некоторого r окажется, что H_σ ^(r) <H_min, то это значит, что требования к надежности сети не выполняются. Число требующих просмотра путей m и сечений r обычно гораздо меньше общего числа путей n и общего числа сечений k (m<<n, k<<r) чем и достигается сокращение трудоемкости оценки. Одновременно гарантируется, что истинное значение надежности сети лежит в заданных пределах H_min≤H₀≤H_max

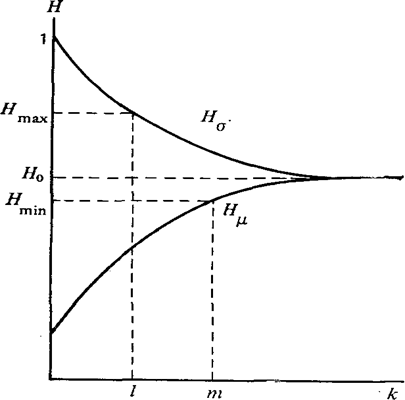
Рисунок 2.5 Характер изменения оценок структурной надежности по совокупности путей и сечений

Точность оценки может быть задана в виде допустимых отклонений от истинного значения H_-b^+a. В этом случае просмотр путей и сечений следует вести до тех пор, пока не выполнится условие. | H_μ ^{(m) -} H_σ ^(r) |≤a+b. В частности, если a=b, то условие прекращения расчетов имеет вид |H_μ ^{(m) -} H_σ ^(r) |≤ ≤2a, а в качестве оценки надежности следует принять величину H= (H_μ ^{(m) -} H_σ ^(r)) /2. В ходе расчетов решения о рассмотрении на следующем шаге очередного пути или сечения целесообразно принимать по критерию большего абсолютного приращения надежности по соответствующему параметру (m или r).

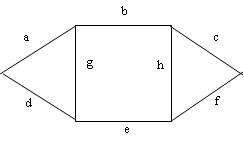
Пример. Пусть необходимо оценить надежность сети, представленной графом на рис.2.6, с точностью H±0,01. Узлы сети идеально надежны. Линии, обозначенные буквами имеют одинаковую надежность p_a=p_b=…p_k=p=0.9.

Выпишем первые несколько путей и сечений, которые могут потребоваться для расчета:

М' = {аЬс, def, abhf, dgbc... };

S' = {ad, be, cf, age... }.

Полные множества путей М и сечений S для рассматриваемого метода можно не выписывать. При необходимости, если на начальном подмножестве М', S' но удается достичь необходимой точности, эти подмножества можно будет расширить по ходу расчетов.

Поскольку первые два пути из М' независимы, можно сразу записать на чальную нижнюю оценку вероятности несвязности сети Q ⁽²⁾ _μ=abc*def= (1-p³) ² ≈0,073. Переходя к оценке надежности, H ⁽²⁾ _μ=1 - Q ⁽²⁾ _μ получаем H ⁽²⁾ _μ=0,927. Начальную верхнюю оценку надежности можно получить по первым трем независимым сечениям множества S':

H_σ ⁽³⁾ =ad*be*cf. (2.26)

При рассмотрении сечений запись вида xyz интерпретируется как наличие, по крайней мере, одного исправного элемента в сечении, поэтому при подстановке исходных данных в (2.26) получим H_σ ⁽³⁾ = [l- (1-p) ²] ³≈0,970. Разница между полученными верхней и нижней оценками составляет |H_σ ^{(3) -} H ⁽²⁾ _μ|=0.044>0.02, поэтому необходимо продолжить расчет.д.обавление следующего пути дает большее абсолютное приращение надежности, чем добавление следующего сечения. Поэтому вводим в рассмотрение очередной путь abhf из множества М' согласно формуле (2.25) Q ⁽³⁾ _μ =abc*def-abhfcde= = (l-p³) ²-p⁴ (1-p) (1-p²). Отсюда получаем очередную оценку надежности снизу. H ⁽³⁾ _μ=1 - Q ⁽³⁾ _μ≈0,939.

Убеждаемся, что заданная точность еще не достигнута и добавление очередного пути снова даст большее абсолютное приращение надежности, поэтому вводим следующий путь dgbc из множества М' для уточнения нижней границы надежности Q ⁽⁴⁾ _μ =Q ⁽³⁾ _μ - dgbcaef= Q ⁽³⁾ _{μ -} p⁴ (1-p) (l-p²) ≈0,049, что соответствует H ⁽⁴⁾ _μ=1 - Q ⁽⁴⁾ _μ≈0,951.

Разница между верхней и нижней оценками надежности теперь составляет-| H_σ ^{(3) -} H ⁽⁴⁾ _μ |=0,019<0,02, что позволяет прекратить расчеты, так как заданная точность H±0,01 достигнута. В качестве оценки надежности рассматриваемой сети принимаем среднеарифметическое H= (H_σ ^{(3) -} H ⁽⁴⁾ _μ) /2=0,962 с гарантией, что 0,961<H₀< 0,963. При этом из полного множества, включающего девять сечений и восемь путей, нам удалось ограничиться рассмотрением всего трех сечений и четырех путей.

Рисунок 2.6 - Пример сети для двусторонней оценки надежности

Для разветвленных сетей связи использование предлагаемого метода позволяет значительно сократить трудоемкость расчетов по сравнению с методом полного перебора путей или сечений. При этом метод гарантирует любой заданный уровень точности оценки вероятности связности сети.

2.2.4 Метод статистической оценки структурной надежности

Широко распространенным методом оценки надежности сложных технических систем является метод статистических испытаний. Однако для получения статистически достоверных результатов, особенно при высокой исходной надежности элементов системы и ее большой структурной избыточности, требуются значительные затраты машинного времени.

Опыт показывает, что основные затраты времени при статистических испытаниях сложной системы сопряжены с проверкой ее работоспособности в каждой реализации. При высокой исходной надежности p_i элементов или большой структурной, избыточности, характерной для разветвленных сетей коммутации, проверка на работоспособность подавляющего большинства реализации дает положительный результат, что обусловливает их малую информативность. Поэтому возникает естественное желание найти некоторое преобразование сети, позволяющее искусственно уменьшить исходную надежность ее элементов, чтобы быстрее набрать необходимую статистику отказов и получить обратное преобразование, позволяющее пересчитывать получаемые результаты на реальные показатели надежности элементов сети. Покажем, что такая возможность действительно существует.

Назовем разрезом подмножество элементов системы, удаление которых приводит к потере работоспособности. Рассмотрим некоторый разрез u, в который входит ровно z элементов. Частота выпадения такого разреза при статистических испытаниях стремится по ходу испытаний к ее вероятности:

P_u=p_i (1-p_j).

Если обозначить через N общее число элементов сети, то вероятность Р_u можно записать в виде

P_u= (p_i)  (1-p_j) /p_j.

Изменим исходные показатели надежности системы таким образом, чтобы каждый сомножитель (1-p_i) /p_j второго произведения увеличился в γ раз. Другими словами, вместо элемента с надежностью p_j введем элемент с надежностью p'_j такой, чтобы удовлетворялось условие

(1-p'_j) /p'_j=γ (1-p_j) /p_{j (}2.27)

При этом из (2.27) надежность нового элемента

p'_j= p_j [p_j+ γ (1 - p_j)] ^-1 (2.28) '

Если произвести преобразование (2.27) для всех элементов сети, то вероятность выпадения разреза u в процессе испытаний изменится и составит

P_u= p_j [p_j+ γ (1 - p_j)] ^-1 γ (1-p_j) /p_j

Введем коэффициент δ увеличения частоты выпадания разреза

δ=P'_u/P_u (2.29)

Подставляя в (2.29) старое и новое значения частоты выпадания разреза u, получаем

δ= p_j [p_j+ γ (1 - p_j)] ^-1 γ.

Если в разрез u входит ровно z элементов, то

δ= γ^z p_j [p_j+ γ (1 - p_j)] ^-1,

где второй сомножитель p_j [p_j+ γ (1 - p_j)] ^-1=K константа для исходной системы. Коэффициент убыстрения можно представить в виде δ=γ^zK. Отсюда следует, что предлагаемое преобразование показателей надежности не приводит к нарушению относительной частоты появления разрезов фиксированного веса z, так как коэффициент убыстрения для всех этих разрезов одинаков. Однако относительная частота появления разрезов веса z+w по сравнению с разрезами веса z увеличивается в γ^w раз. Поэтому в ходе статистических испытаний преобразованной системы можно набрать достаточную статистику по разрезам большего веса, вероятность появления которых в исходной системе бывает обычно очень малой.

Пересчет вероятности появления разреза u из преобразованной системы в исходную производится в соответствии с (2.29):

P_u=P'_u/δ=P'_uγ^-zK^-1 (2.30)

Для выполнения обратного преобразования (2.30) кроме факта отказа системы необходимо фиксировать и вес z соответствующего разреза.

Из (6.30) следует, что каждый случай появления разреза u с весом z в преобразованной системе соответствует γ^-zK^-1 случаям появления такого же разреза в исходной системе. При этом если; д преобразованной системе за время испытаний произошло m отказов, то для исходной системы эквивалентное число отказов.

m_экв=K^-1γ^-zi,

где z_i - число элементов, вышедших из строя при i-м отказе системы.

При возникновении очередного m-го отказа в преобразованной системе оценки надежности Р_m исходной системы уточняются в соответствии с выражением.

P_m=1-m_экв/M=1- (MK) - ¹ γ^-zi,

где М - общее число просмотренных реализации состояний преобразованной системы.

Возникает вопрос, каким следует выбирать параметр преобразования γ для максимального убыстрения. процесса статистических испытаний конкретной системы? Из (2.28) следует, что при γ=1 изменение исходной надежности не происходит и убыстрение отсутствует. Если выбрать γ слишком большим, то в преобразованной системе будут в основном возникать разрезы большого веса, не характерные для исходной системы, причем их вклад в результирующую надежность при больших z в соответствии с (2.30) будет невелик. Поэтому параметр γ следует выбирать таким образом, чтобы максимизировать вероятность возникновения наиболее "вероятных" разрезов.

Рассмотрим этот вопрос более подробно.

Для простоты положим, что показатели надежности всех элементов системы одинаковы и равны р. Обозначим через P (z) вероятность возникновения отказовых состояний веса z. Очевидно, что вероятность потери работоспособности системы

Q=  P (z). (2.31)

Обычно для реальных систем значение P (z) достаточно плавно меняется с увеличением веса разреза, поэтому в качестве наиболее вероятного разреза можно выбрать класс разрезов среднего веса.

Z_cp= [zP (z)] /P (z).

Для надежных систем в выражении (2.31) можно пренебречь всеми членами, кроме первого ненулевого, соответствующего минимальному разрезу веса z₀, который и будет наиболее вероятным. Таким образом, задача состоит в том, чтобы максимизировать коэффициент убыстрения для наиболее вероятного разреза, т.е. найти максимум функции δ _(γ) при z=z_0, p_i=p, (i=1,2,…,N):

δ _(γ) =γ^z0 [p+γ (1-p)] ^-N. (2.32)

Из условия ∂δ _(γ) /∂γ=0 получаем оптимальное значение

γ₀=z₀p [ (N-z₀) / (1-p)] ^-1 (2.33)

Подставляя (2.33) в (2.28), нетрудно убедиться, что оптимальное значение γ₀ соответствует пересчитанному значению надежности элемента системы p'=1-z₀/N. Другими словами, для максимального убыстрения процедуры статистических испытаний необходимо таким образом пересчитать надежность элементов системы, чтобы средний вес отказов в преобразованной системе соответствовал весу наиболее вероятного разреза.

Убыстрение темпа набора статистики отказов в соответствии с (6.32) составит

δ_m={z₀/ [ (1-p) N] }^z0 [ (N-z₀) / (pN)] ^N-z0.

Так, для системы с параметрами p=0,99, N=20, z₀=3 время испытаний можно сократить приблизительно в 150 раз для достоверности получаемых результатов не хуже, чем в случае прямого набора статистики отказов системы.

Проведенные на ЭВМ сравнительные статистические испытания конкретных сетей по обычному и предлагаемому методам показали, что убыстрение сходимости результатов испытаний соответствует приведенным теоретическим оценкам.

3. Исследования структурной надежности радиотехнических систем методом статистического моделирования 3.1 Критерии оценки структурной надежности радиотехнических систем методом статистического моделирования

Критерием оценки структурной надежности сетей связи методом статистического моделирования является вероятность наступления события - сеть связана.

На сегодняшний день в литературе известно несколько методов проверки сетей на связность: “поиск в глубину”, “разрастания” и “свертки”.

Известно, что метод “свертки” позволяет уменьшить до 50% (по сравнению с другими методами) затраты времени ЭВМ для данной процедуры. Суть данного метода заключается - одновременное соединение инцидентных вершин с произвольно выбранной вершиной до тех пор, пока сеть не представится в виде одной точки (если сеть связна) или множество точек (если сеть несвязна).

Однако методу, как и другим, присущ недостаток - резкое (нелинейное) увеличение затрат времени ЭВМ (по сравнению с другими методами) на процедуру проверки графа сети на связность.

Метод “разбиения". Суть метода “разбиения” состоит в следующем. Граф сети разбивается на подграфы, каждый из которых отдельно проверяется на связность методом “свертки". В результате получаем новый граф - суперграф, который в свою очередь проверяется на связность. Если суперграф связен, то делается вывод, что исходный граф сети связен. За счет “разбиения” исходного графа сети на подграфы появляется возможность работать на пологом участке кривой, отображающей зависимость затрат времени ЭВМ от размерности графа.

Оценка сложности метода “разбиения". Рассмотрим граф сети в виде квадратной решеткою Конечно, едва ли следует ожидать, что граф реальной сети будет иметь структуру с квадратной ячейкой. Однако оценки, полученные для данной ситуации, дадут представления о сложности предлагаемого метода проверки графа сети на связность. Вложим данный граф в прямоугольную систему координат.д.опустим, число вершин по осям x и y одинаково и равно L. Общее число вершин в графе будет равно S=L²

В данном случае по методу “свертки” достаточно выполнить

L-1=

итераций для определения связности графа. Тогда сложность метода “свертка” будет определятся

Q=M (),

где M - степень каждой вершины графа.

Допустим, что граф разбит на n равных подграфов, тогда сложность

проверки каждого подграфа составит

G₁=M (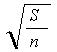-1)

Учитывая проверку на связность полученного суперграфа, размерность которого равна n, получим оценку сложности метода “разбиения"

Q_n=M (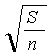-1) +M (-1).

3.2 Разработка алгоритма оценки структурной надежности радиотехнических систем методом статистического моделирования

Сеть связи задают в виде вероятностной матрицы смежности

P=||pij||s,s, где Pij=kg (i,j) (i,j=1…S; i¹j).

Осуществляет NO независимых испытаний, каждое из которых состоит из двух этапов. На первом этапе выбирают m независимых, равномерно распределенных в интервале (0,1) чисел X_i. Затем, значения X_i последовательно сравнивают с величинами k_г (i,j) по следующему алгоритму:

Если xi ³ k_г (i,j), то элемент сети считается отказавшим (Aij=0);

Если xi < k_г (i,j), то элемент сети находится в исправном состоянии (Aij=1).

Второй этап - проверка структуры, полуученой в результате выхода ее элементов из строя, на связность. Если сеть связана, то исход испытаний относится к числу благоприятных. Отношения числа благоприятных исходов к общему числу испытаний NO и будет оценкой структурной надежности анализируемой сети связи.

Процедура проверки сети на связность состоит в следующем. На анализируемой сети связи выбирается произвольный узел коммутации. Далее одновременно соединяют соседние узлы коммутаций к первоначально выбранному. Эта процедура осуществляется до тех пор, пока сеть не представится в виде одинокой точки (в случаи, если сеть связна) или множество точек (если сеть не связна). Данный метод получил названия метода ’’Соединения’’.

Алгоритм проверки сети на связность методом “свертки", состоит из следующих операций:

Выбор произвольного узла коммутаций (вектор-строки a_p) матрицы A=║a_ij║_s,s.

Запись выбранного номера узла коммутаций a_p в одномерный массив P (1), который имеет размерность S.

Определение соседних узлов коммутаций: a₁,...,a_R, где R - степень узлов коммутаций. Если соседних узлов коммутаций нет, то переходим к шагу 7.

Проверка наличия номеров соседних узлов коммутаций в массиве P (1). Отсутствующие номера записываем в массив P (1).

Формируем новый вектор-строку a¹_p=a₁Úa₂Ú...Úa_RÚa_p.

Проверяем: a_p=1→сеть считается связной; a_p¹≠1→возвращяемся к шагу номер 3.

Проверяем: массив Р (1) заполнен весь? Если да, то сеть считается связной. В противном случае сеть несвязна.

Изобразим алгоритм оценки структурной надежности радиотехнических систем методом статистического моделирования.

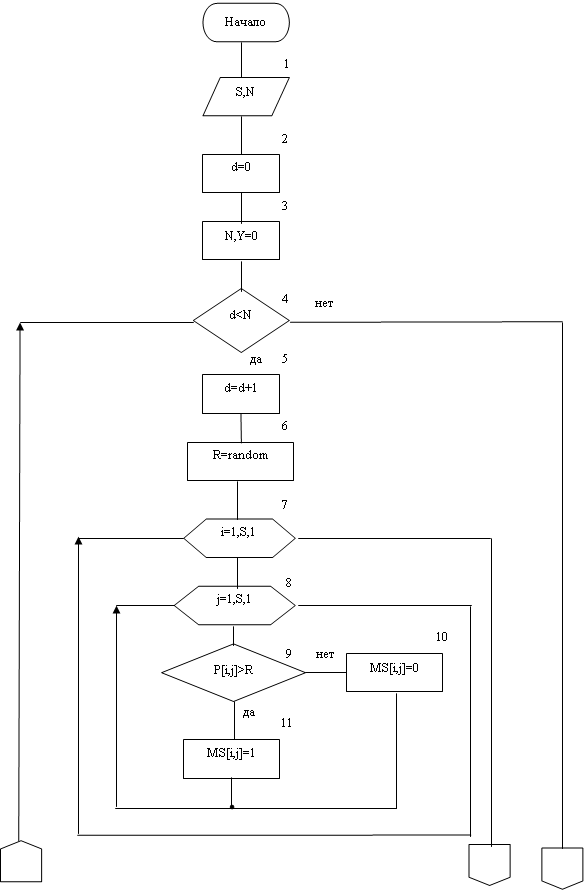
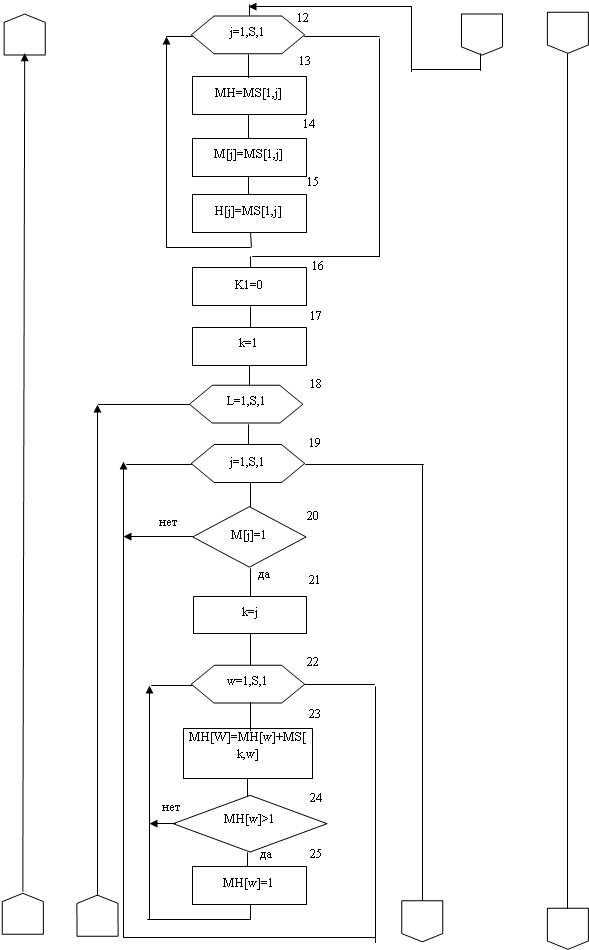
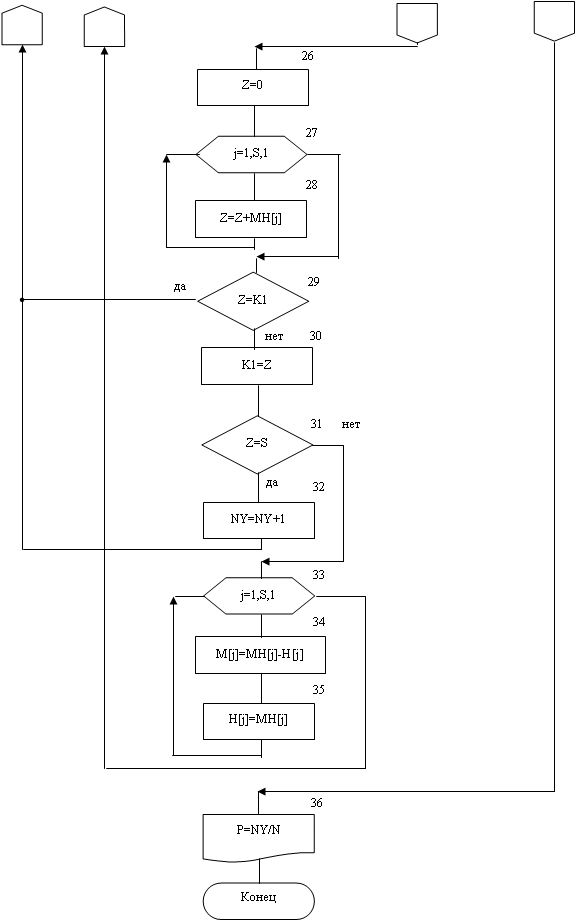
3.3 Разработка программы оценки структурной надежности радиотехнических систем методом статистического

Начинаем программу с описания переменных, которые мы будем использовать походу программы. Задаем два двухмерных массива, которые понадобятся нам для описания матрицы ”смежности” и три одномерных массива, которые будем использовать при процедуре ”свертки".

С помощью процедуры ” kol_node ” мы осуществляем ввод количества узлов анализируемой системы. А с помощью процедуры ”kol_attemp ” задаем необходимое количество испытаний.

Процедуру ” number_attemp ” начинаем с обнуления всех используемых массивов т.к программа хранит данные о испытаниях. Далее мы при помощи двух циклов for, задаем матрицу ”смежности” двумя способами: автоматически (param=1) или вручную (param=2). Цикл ”while d<N" выполняется до тех пор, пока не выполнятся все испытания. Потом, с помощью генератора случайных чисел задаем переменную ”R” в интервале от 0 до 1, затем сравниваем значения ”R” с элементами матрицы ”смежности”. Если R больше элемента, то значению элемента матрицы смежности присваевается единица, а если R меньше, то элементу присваевается ноль. Далее проводим процедуру проверки сети на ”связность”. Если при сложений элементов первой строки матрицы, мы получим ноль, то проводить процедуру свертки не надо т.к сеть ”несвязна". Переходим к следующему испытанию. Но, а если при сложение всех элементов строки получим сумму равную количеству элементов, то тогда сеть связна. При наличие в строке как нулевых, так и единичных элементов, мы проводим процедуру свертки. В первой строке находим единичный элемент, по положению которого определяем с номером какой строкой строки мы будем складывать первую строку. Полученную в результате строку проверяем на связность. Если она несвязна, то повторяем операцию сложения (полученную строку складываем со следующей строкой). Операцию проводим до тех пор, пока все элементы в строке не будут равны единицы или пока все строки не будут стянуты в одну. При проверки сети на связность, мы используем три одномерных массива. В массиве ”h” мы храним информацию о строках стянутых на предыдущем шаге, в массив ”mh" заносятся номера всех строк которые стянуты, а массив ”m” мы используем как промежуточный, в нем записана информация о еще не стянутых строках.

Далее мы описываем процедуру MENU. Которая обеспечивает доступ к соответствующим процедурам, отвечающим за ввод данных и ввывод результатов.

Тело программы включает в себя только обращение к процедуре MENU.

4. Расчет себестоимости

В данном проекте разработано программное обеспечение лабораторной работы на тему ” Исследование структурной надежности РТС". Ввиду отсутствия информации о подобных разработках осуществить сравнение данного продукта с аналогом не представляется возможным. Поэтому произведём расчёт себестоимости программы.

Себестоимость программного обеспечения можно определить по формуле 4.1:

С= (З / m) K (t₁+t₂) (1+K_н) + 8 t₃ С_м, (4.1)

где С - себестоимость программного обеспечения;

З - среднемесячная заработная плата разработчика программы, (руб);

m - среднее количество рабочих дней в месяце;

К - коэффициент, учитывающий отчисления во внебюджетные фонды:

Пенсионный-28%.

Фонд занятости-1.5%

Фонд страхования-5.4%

Фонд мед. страхования-3.6%

Итого 38.5%, К=1.385

t₁ - время, затраченное разработчиком в днях: