Навигация
Модель відгуку плоскої ЦАР
2.2. Модель відгуку плоскої ЦАР
Відгук плоскої ЦАР для варіанта 2-координатної процедури оцінювання можна формалізувати за допомогою “натягнення” вектора А комплексних амплітуд М сигналів на діагональ одиничної матриці: ![]() [29]. Згідно [29], аналітична модель відгуку плоскої решітки у матричній формі при одновідліковому вимірі напрямку на М сигналів має вигляд:
[29]. Згідно [29], аналітична модель відгуку плоскої решітки у матричній формі при одновідліковому вимірі напрямку на М сигналів має вигляд:
![]() , (13)
, (13)
де ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() - матриці ПХ каналів ЦАР у напрямках М сигналів, відповідно в вертикальній і горизонтальній площинах,
- матриці ПХ каналів ЦАР у напрямках М сигналів, відповідно в вертикальній і горизонтальній площинах,
![]() ,
, ![]() - матриці КВВ, відповідно в вертикальній і горизонтальній площинах.
- матриці КВВ, відповідно в вертикальній і горизонтальній площинах.
З урахуванням впливу шуму та (12), аналітичну модель відгуку плоскої ЦАР за умови взаємного впливу АЕ (13) можливо записати за виразом:
![]() , (14)
, (14)
де ![]() - адитивний шум.
- адитивний шум.
Однак, зі збільшенням розмірності прийнятої моделі сигналів формалізація істотно ускладнюється, що істотно впливає на можливість практичної реалізації вказаної моделі відгуку антенної решітки. Для вирішення цього питання в разі проведення багатокоординатних (наприклад: три, чотири координати) необхідно застосовувати більш розвинутий матричний апарат - сімейство торцевих добутків матриць, який був запропонований в [29].
Згідно [29], торцевим добутком hxg–матриці V (![]() ) і
) і ![]() – матриці W, що представлена як блок–матриця строк [
– матриці W, що представлена як блок–матриця строк [![]() ] (W=[
] (W=[![]() ],
], ![]() ), є hxgd–матриця V□W, що визначається рівністю:
), є hxgd–матриця V□W, що визначається рівністю:
V □ W = [![]() ]
(15)
]
(15)
Приклад. 1
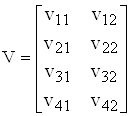 ,
,  ,
,
V□W =  .
.
Відгук плоскої ЦАР у випадку незалежності КВВ від напрямку приходу сигналів і проведення 2-координатних (наприклад, за двома кутами) вимірів можна представити аналогічно лінійній ЦАР (12) [28]:
![]() , (16)
, (16)
де ![]() □
□![]() ,
,
A - вектор оцінок комплексних амплітуд М сигналів,
U - блок-вектор комплексних напруг приймальних каналів ЦАР,
![]() ,
, ![]() - матриці ПХ каналів ЦАР, відповідно в вертикальній та горизонтальній площинах, наприклад:
- матриці ПХ каналів ЦАР, відповідно в вертикальній та горизонтальній площинах, наприклад:
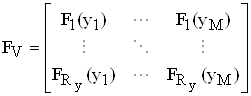 ,
, 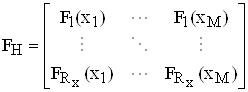 ,
,
![]() ,
, ![]() - матриці КВВ, що не залежать від кутової координати, відповідно в вертикальній і горизонтальній площинах,
- матриці КВВ, що не залежать від кутової координати, відповідно в вертикальній і горизонтальній площинах,
![]() ,
, ![]() - кількість просторових каналів плоскої ЦАР відповідно по вертикалі та горизонталі (див. рис.1.6),
- кількість просторових каналів плоскої ЦАР відповідно по вертикалі та горизонталі (див. рис.1.6),
![]() ,
, ![]() - кутові координати напрямку приходу m-го сигналу,
- кутові координати напрямку приходу m-го сигналу,
М - кількість сигналів,
□ - торцевий добуток матриць.
Крім (15), слід розглянути його транспоновану модифікацію [29]. Транспонованим торцевим добутком (ТТД) ![]() –матриці V (
–матриці V (![]() ) і
) і ![]() –матриці W, що представлена як блок–матриця стовпців [
–матриці W, що представлена як блок–матриця стовпців [![]() ] (W=[
] (W=[![]() ],
], ![]() ), є
), є ![]() –матриця V■W, що визначається рівністю:
–матриця V■W, що визначається рівністю:
V■W = [![]() ]
(17)
]
(17)
Приклад. 2
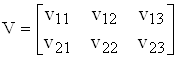 ,
, 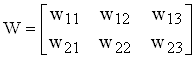 ,
,
V■W = 
Згідно [29], для (15) та (17) дійсно: ![]() □
□![]() =
=![]() ■
■![]() . В частковому випадку, коли V та W - вектори, має місце властивість:
. В частковому випадку, коли V та W - вектори, має місце властивість:
![]() □
□![]() =
=![]() , (18)
, (18)
де ![]() - кронекеровський добуток.
- кронекеровський добуток.
Вираз (17) також має назву операції Khatri-Rao [29].
Матриця Р у виразі (16) при використанні ТТД має вигляд:
![]() , (19)
, (19)
де ![]() ■
■![]() .
.
Без втрати спільності, відгук антенної решітки можна розвинути на випадок трьох, чотирьох і більше координат (параметрів). При цьому буде змінюватися лише представлення матриці Р, що дуже спрощує застосування та узгодження відомих однокоординатних процедур у більш складних завданнях.
0 комментариев