Выдача сигнала на ЦАП, вычисление спектра сигнала с высоким разрешением по частоте, графическое представление результатов обработки

6. Выдача сигнала на ЦАП, вычисление спектра сигнала с высоким разрешением по частоте, графическое представление результатов обработки.

4.3 Расчет выходных эффектов тракта

Сформированный указанным выше способом сигнал на элементах антенны «нарезается» на временные фрагменты длиной n=512 точек с учетом перекрытия, которое вводится в модель тракта как параметр. Каждый фрагмент подвергается процедуре БПФ, в результате чего получаются спектры процессов на выходе приемных элементов. Из получившегося набора частот в дальнейшую обработку берутся только номера частот fk, соответствующие заданной полосе обработки (fнчfв).

Как было показано выше, вырезание полосы фильтром с прямоугольной частотной характеристикой вносит дополнительные искажения в восстановленный сигнал. Поэтому в модели предусмотрено расширение полосы обработки от значения (0,3-4,5) кГц до (0,05-5) кГц.

На следующем этапе происходит формирование канала наблюдения в частотной области путем сложения спектров реализаций с приемных элементов АР, умноженных на заранее рассчитанные фазирующие коэффициенты на это направление.

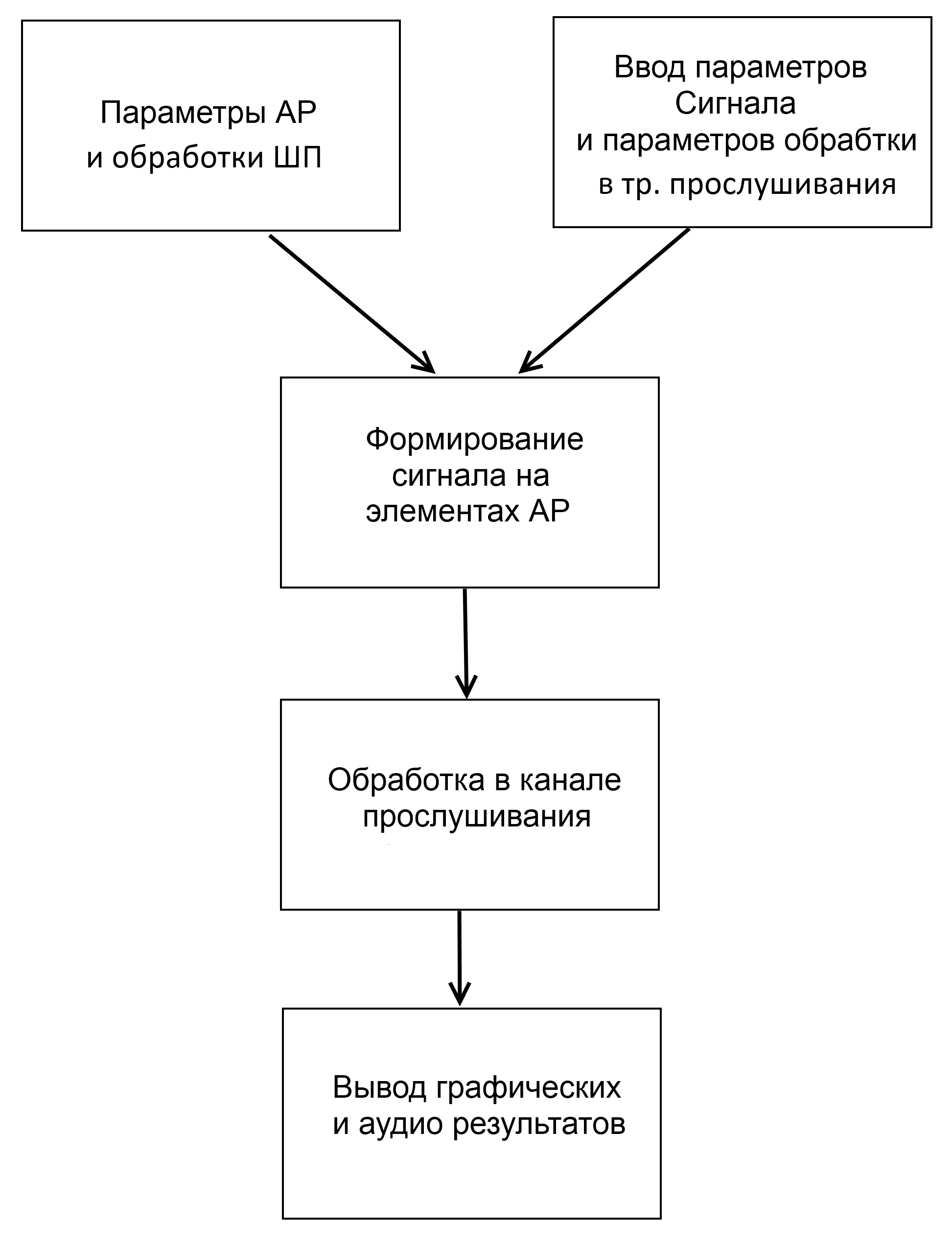
Рис. 19 Структурная схема программного макета тракта прослушивания

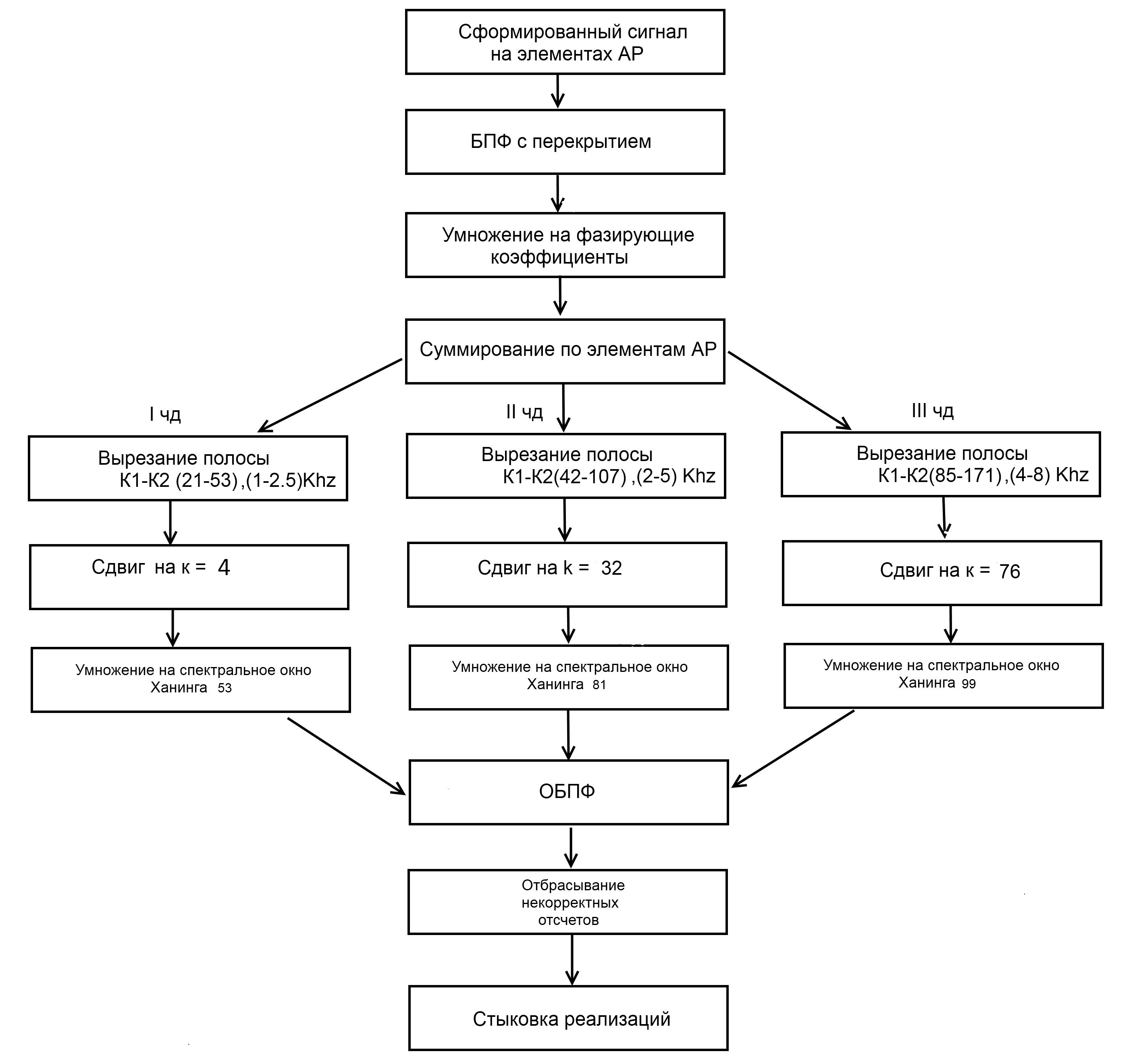
Рис.20 Обработка в канале прослушивания

После ФХН выполняется вырезание полосы частот выбранного частотного диапазона и сдвиг ее на заранее рассчитанное для каждого ЧД число спектральных отсчетов. Затем проводится процедура ОБПФ, на выходе которой получаем временную реализацию. Как было показано ранее, для устранения эффектов, вызванных вырезанием полосы частот, необходимо перед восстановлением сигнала во временную область ввести частотное окно, вид которого в модели можно выбирать из заранее созданных файлов либо из имеющегося в системе MatLab банка частотных фильтров, а также задавать их параметры. В модели тракта прослушивания параллельно формируются и обрабатываются сигналы, восстановленные с применением частотного окна и без него.

Восстановленный сигнал содержит в себе некорректные отсчеты. Фазирующие коэффициенты, используемые при формировании веера пространственных каналов, таковы, что длительность “испорченных” фрагментов реализации в начале и в конце ее приблизительно одинакова. Поэтому из реализации исключаются некорректные отсчеты в начале и в конце кусочка реализации длиной n отсчетов.

Для сокращения времени моделирования, а также экономии внутренней памяти MatLab сигнал на приемных элементах АР моделируется на ограниченном временном интервале, причем длина этого интервала должна быть достаточной для формирования оценки спектральной плотности мощности процесса с требуемым частотным разрешением. Длина такой реализации в программе определяется автоматически с учетом необходимого количества точек перекрытия и количества точек.

5 Результаты расчетов

Чтобы сформировать сигнал на элементах АР нужно рассчитать задержки на каждом элементе и сымитировать их.

Исходя из заданных нами параметров, система формирует приходящий на АР сигнал под определенным углом.

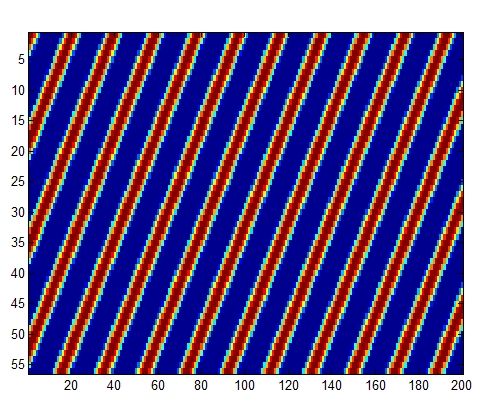
Рис.22 Приход сигнала под углом на элементы АР

Обработка в канале прослушивания

Блок основных вычислительных операций подробно будет рассмотрен далее.

Вывод графических и аудио результатов

После обработки мы можем прослушать и наглядно увидеть графики сигналов, изначально пришедших на элементы АР, и вычисляем спектры восстановленных сигналов с высоким частотным разрешением, частное разрешение системы определяется длительностью реализации взятой в обработку.

По сформированным входным воздействиям реализуется обработка в канале прослушивания .

Сформированный сигнал на элементах АР

Исходя из заданных нами параметров, система формирует приходящий на АР сигнал под определенным углом.

БПФ с перекрытием

Выполняется БПФ с перекрытием, перекрытие задается произвольным, либо кратно числу точек БПФ (как и выяснилось в результате моделирования), но задать перекрытие мы можем произвольно. Выполняется перекрытие на каждом приемном элементе АР.

Умножение на фазирующие коэффициенты

Этап процедуры формирования. внесение задержек в частотной области

Суммирование по элементам АР

Вырезание полосы

Поскольку у нас частотное окно имеет спады на краях диапазона, мы расширяем полосу сигнала, чтобы не сильно зарезать энергетику сигнала.

Сдвиг

В первом частотном диапазоне полоса частот 1-2,5 кГц это соответствует спектральным отсчетам: К нижнее =21, К верхнее =53. В соответствии с такой закономерностью сдвигать при выбранной величине перекрытия мы можем только порциями по 4Δf значит первый спектральный отсчет ,для того чтобы попасть в полосу 3-3.5 кГц должен быть сдвинут на 4 отсчетов . Соответственно для второго диапазона 2-5 кГц : К нижнее =42, К верхнее =107 , 32 отсчетов. Для третьего 4-8 Кгц: К нижнее =85, К верхнее =171, 76 отсчетов.

Рассчитывать коэффициент сдвига будем проводить по формуле

Где нижнее значение частотного диапазона,

= коэффициент фильтра,- число сдвига спектральных отсчетов.

7 – коэффициент минимальной частоты переноса спектра = 300 ГЦ

Умножение на спектральное окно

Для каждого из трех диапазонов мы выбираем свои параметры фильтра . В данной случае будем менять лишь параметры фильтра Ханна (53 81 99). Полученные по формуле:

K=kB-kH+2*kl+1

ОБПФ

Обратное преобразование Фурье с количеством точек равным в БПФ

Отбрасывание некорректных отсчетов

Формирование делалось таким образом, чтобы некорректные отчеты равномерно распределялись вначале и в конце реализации поэтому половину отчетов мы убираем из начала реализации и из конца.

Стыковка реализаций

В результате получаем реализацию большой длительности, которая подвергается преобразованию Фурье.

MATLAB - это интерактивная система, в которой основным элементом данных является массив. Это позволяет решать различные задачи, связанные с техническими вычислениями, особенно в которых используются матрицы и вектора, в несколько раз быстрее, чем при написании программ с использованием "скалярных" языков программирования, таких как Си или Фортран.

В результате работы программы мы получаем следующие результаты :

Для первого частотного диапазона (1-2.5) Khz

Каждый частотный диапазон соответствует спектральным отсчетам k1=[21] k2=[53]

Угол прихода сигнала берем равный Pi/4

Сдвиг полосы в область от 0.3 , 4Δf = 187 Гц

Умножение на спектральное окно K=53

Частота сигнала 2000 Гц

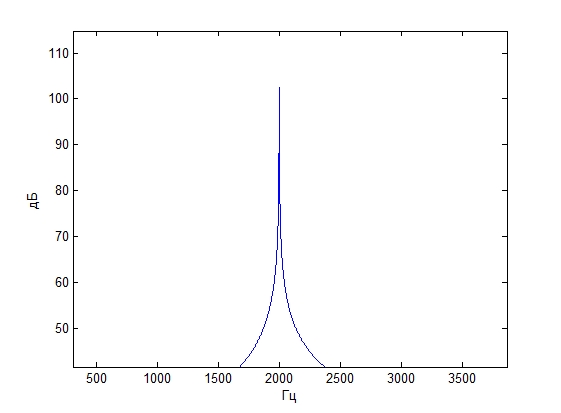
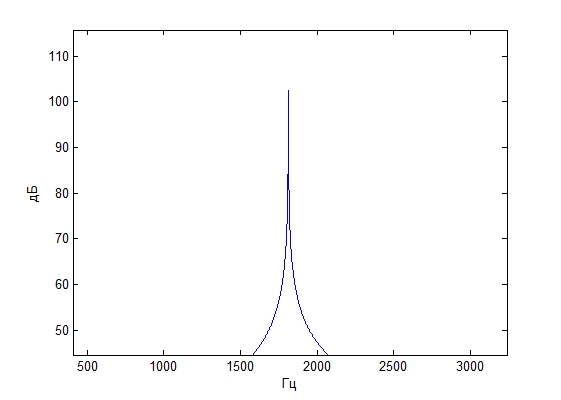
Спектр исходного сигнала Спектр восстановленного сигнала

со сдвигом

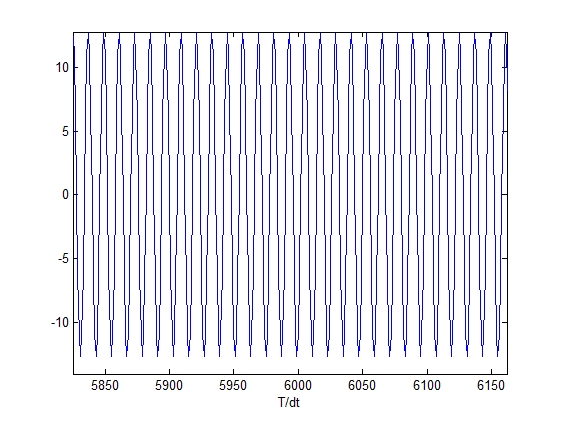
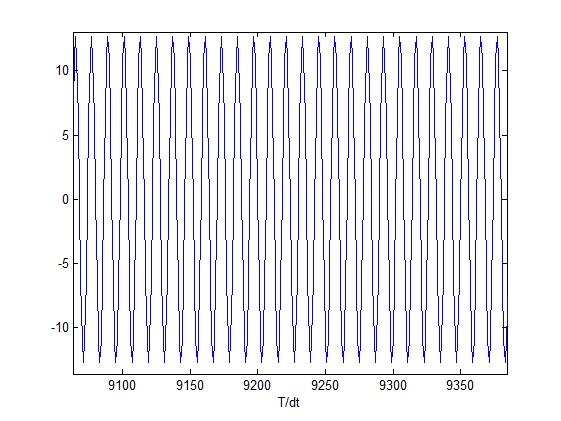
Исходный сигнал во временной области Восстановленный сигнал во

временной области

Для второго частотного диапазона (2-5) Khz

Каждый частотный диапазон соответствует спектральным отсчетам k2=[42] k2=[107]

Угол прихода сигнала берем равный Pi/4

Сдвиг полосы в область от 0.3 , 32Δf = 1500 Гц

Умножение на спектральное окно K=81

Частота сигнала 3500 Гц

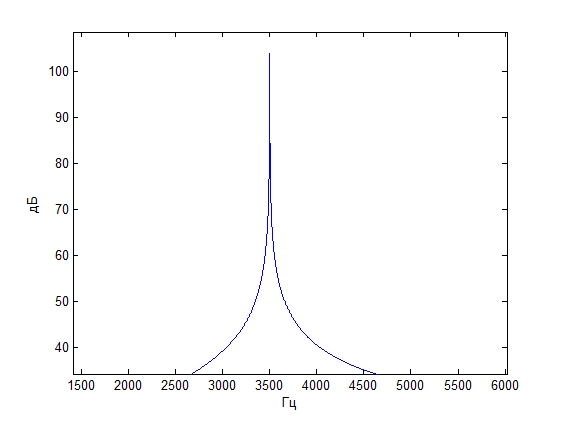
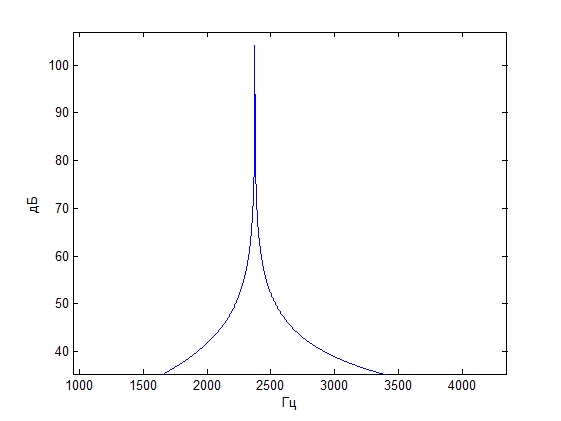
Спектр исходного сигнала Спектр восстановленного

сигнала со сдвигом

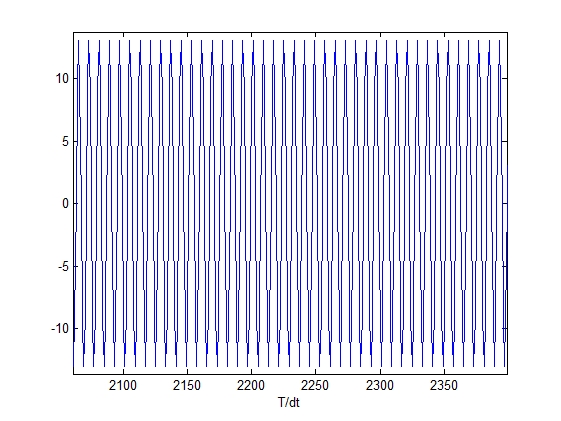
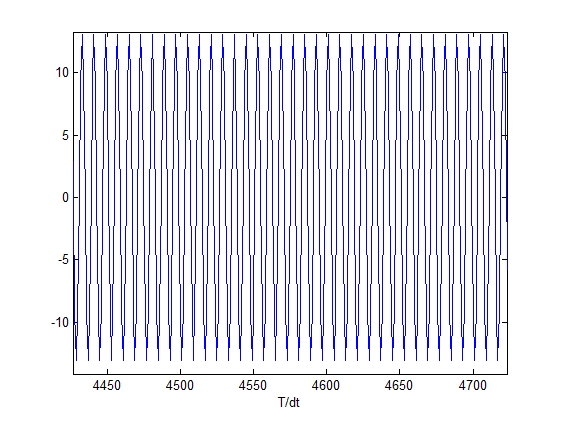
Исходный сигнал во Восстановленный сигнал

временной области во временной области

Для третьего частотного диапазона (4-8) Khz

Каждый частотный диапазон соответствует спектральным отсчетам k2=[85] k2=[171]

Угол прихода сигнала берем равный Pi/4

Сдвиг полосы в область от 0.3 , 76Δf = 3570 Гц

Умножение на спектральное окно K=99

Частота сигнала 5000 Гц

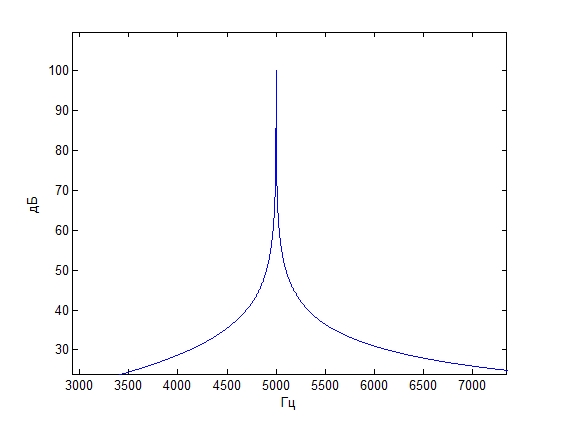
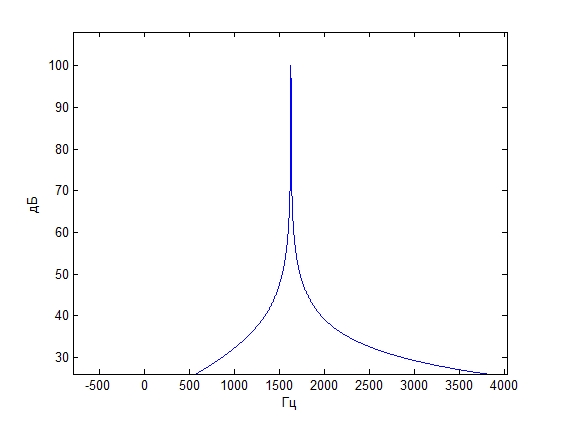
Спектр исходного сигнала Спектр восстановленного

сигнала со сдвигом

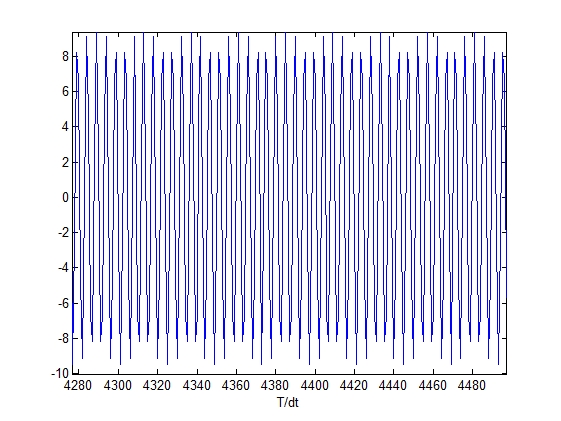
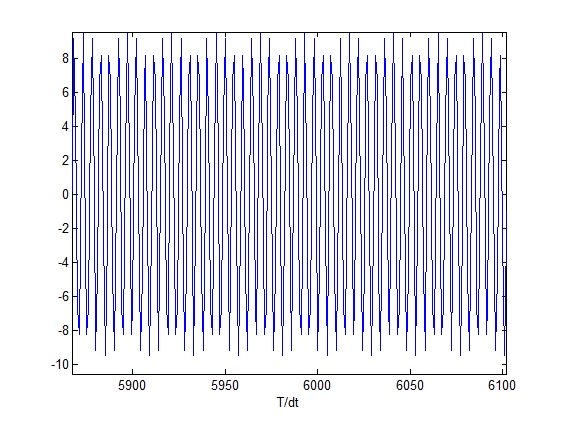
Исходный сигнал во временной Восстановленный сигнал

области во временной области

Виды частотных окон Ханна ИПХ фильтров Ханна

для трех диапазонов для трех диапазонов

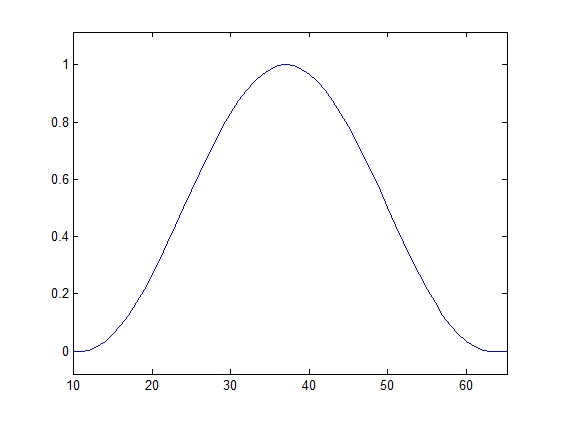
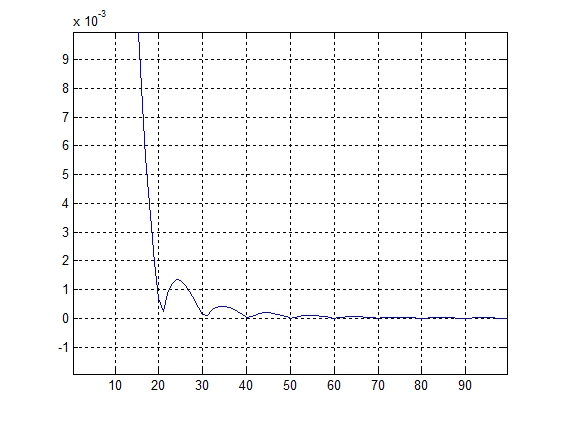
Для первого диапазона (1-2.5) кГц

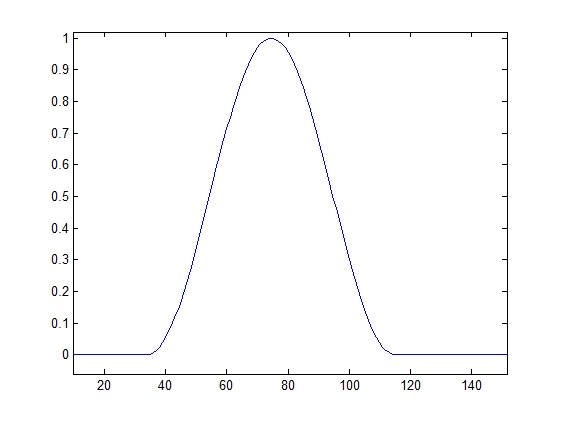
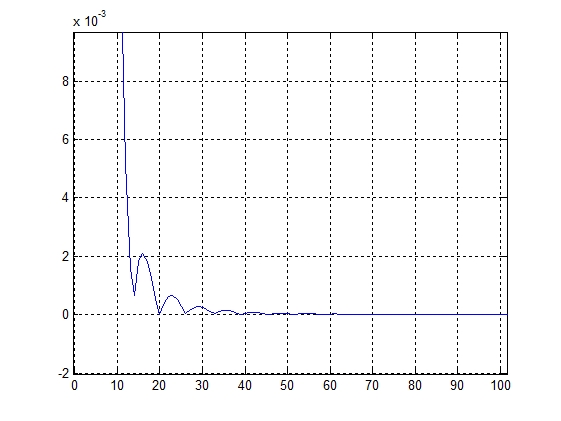
Для второго диапазона (2-5) кГц

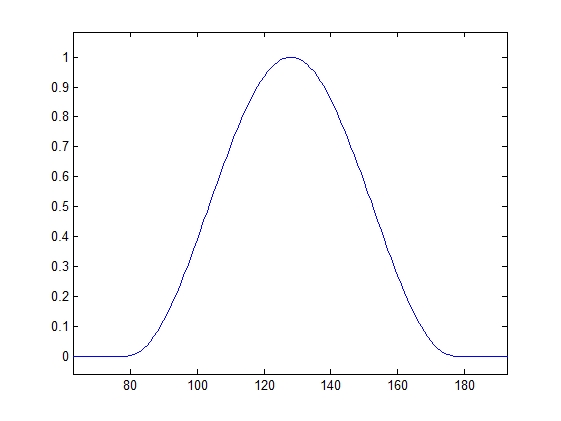
Для третьего диапазона (4-8) кГц.

Заключение

В данной работе была разработана структура тракта прослушивания гидроакустических сигналов на выходе сформированного пространственного канала (канала наблюдения) в тракте шумопеленгования с использованием многоэлементной антенной решетки для трех частотных диапазонов.

Разработан программный макет тракта прослушивания, удовлетворяющий всем требования для моделирования сигналов и процессов их обработки в тракте ШП.

Установлена взаимосвязь основных параметров тракта прослушивания с базовыми параметрами тракта ШП.

Требования задания полностью выполнены и подтверждены графиками, полученными в результате моделирования.

Список литературы

Липатов В.В. Электромагнитные поля в морской воде [Книга]. - Ленинград : ГМТУ, 1990.

Рогожников К. И. Морские информационные системы [Книга]. - Санкт-Петербург : АМУР-ПРЕСС, 2002. - стр. 106.

Лоскутова Г.В., Полканов К.И. Пространственно-частотные и частотно – волновые методы описания и обработки гидроакустических полей. [Книга]. - Санкт-Петербург .: Наука, 2007.-239с.

Ю.А.Корякин, С.А. Смирнов, Г.В.Яковлев. Корабельная гидроакустическая техника: состояние и актуальные проблемы.- СПб.:Наука.-410с.

Марпл-мл.С.Л. Цифровой спектральный анализ и его приложения. М.: Мир, 1990.

Смарышев М.Д. Направленность гидроакустических антенн. Л. Судостроение, 1973.

Гусев В.Г. Системы пространственно-временной обработки гидроакустической информации. Л.: Судостроение, 1988 г.

Дьяконов В.П., MATLAB 6 универсальная интегрированная система компьютерной математики. С-Пб: Питер, 2001 г.

Лазарев Ю.А. Моделирование процессов и систем в MATLAB. СПб.: Питер, 2005 г

Поршнев С.В. MATLAB 7. Основы работы и программирования. М.: Бином-Пресс, 2006 г.

Сергиенко А.Б. Цифровая обработка сигналов. СПб.: Питер, 2003 г.

Приложение 1. Текст программы в Matlab

fd=24000;

dt=1/fd;

t=(0:dt:2);

d=0.1;

c=1500;

n=512;

M=30;

jk=sqrt(-1);

df=fd/n;

fk=df*(0:n-1);

f=input ('введите частоту сигнала (1-2.5)kHz-I чд,(2-5)kHz-II чд,(4-8)kHz-III чд =');

fk0=floor(f/df+0.5);

nd=input('Введите номер диапазона=');

k1=[21 42 85];

k2=[53 107 171];

k0_=[7 10 7];

kl_=[10 8 6];

kH=k1(nd);

kB=k2(nd);

kl=kl_(nd);

k0=k0_(nd);

fm=5;

am=0.0;

al=-pi/4;

s=cos(2*pi*f*t);

s=cos(2*pi*f*t).*(1+am*cos(2*pi*fm*t));

tau0=d/c*sin(al);

tau=(0:M-1)'*tau0;

Ttau=repmat(tau,1,size(t,2));

%sound (s,fd)

T=repmat(t,M,1);

x=cos(2*pi*f*(T-Ttau)).*(1+am*cos(2*pi*fm*(T-Ttau)));

fk1=[fk(1:n/2+1) fk(n/2+2:n)-fd];

kolf=exp(jk*2*pi*tau*fk1);

fo=zeros(1,n);

fo(kH-kl:kB+kl)= hann (kB-kH+2*kl+1);

Ro=repmat(fo,M,1);

Per=1*n/2;

n_per=n-Per;

K=Per/2+1;

for i=1:100;

In=(i-1)*n_per+1;

Ik=In+n-1;

Y0=fft(x(:,In:Ik),n,2);

Y=Y0.*Ro;

z=sum(Y.*kolf,1);

V=zeros(1,n);

V(k0:k0+kB-kH+2*kl)=z(kH-kl:kB+kl);

U=ifft(z,n);

Ik1=i*n_per; In1=(i-1)*n_per+1;

w(In1:Ik1)=real(U(K:K+n_per-1));

U=ifft(V,n);

w1(In1:Ik1)=real(U(K:K+n_per-1));

end

nBCE=size(w,2);

figure,plot(fd/nBCE*(0:nBCE-1),20*log10(abs(fft(w))));

xlabel('Гц')

ylabel('дБ')

figure, plot (w)

xlabel('T/dt')

sound (w,fd);

figure,plot(fd/nBCE*(0:nBCE-1),20*log10(abs(fft(w1))));

xlabel('Гц')

ylabel('дБ')

figure, plot (w1)

xlabel('T/dt')

sound (w1,fd);

figure,plot(abs(ifft(fo,512))),grid on;

figure,plot (fo);

fd=24000;
dt=1/fd;
t=(0:dt:2); %массив времен
d=0.1;% шаг между приемниками АР
c=1500;

n=512; % число точек БПФ
M=30; %кол во элементов АР (линейная)
jk=sqrt(-1); %мнимая еденица
df=fd/n; %частотное разрешение системы
fk=df*(0:n-1); %массив частот после преобр фурье

f=input ('введите частоту сигнала (1-2.5)kHz-I чд,(2-5)kHz-II чд,(4-8)kHz-III чд =');
fk0=floor(f/df+0.5);
nd=input('Введите номер диапазона=');
k1=[21 42 85];%Начальные номера диапазонов
k2=[53 107 171];%Конечные номера длиапазона
k0_=[7 10 7];
kl_=[10 8 6];
kH=k1(nd);
kB=k2(nd);
kl=kl_(nd);
k0=k0_(nd);
fm=5;
am=0.0;
al=-pi/4; % угол прихода сигнала
s=cos(2*pi*f*t); % сигнал в поле в точке значения
s=cos(2*pi*f*t).*(1+am*cos(2*pi*fm*t));
tau0=d/c*sin(al); %Задержка сигнала между соседними приемными элементами
tau=(0:M-1)'*tau0;% массив задержек

Ttau=repmat(tau,1,size(t,2)); %формируем массив задержек размножаем на все моменты времени на 1 сек
%sound (s,fd)
T=repmat(t,M,1);% размножили время на M приемных элементов
x=cos(2*pi*f*(T-Ttau)).*(1+am*cos(2*pi*fm*(T-Ttau))); %сигнал на элементах АР приходящий с направления альфа
%figure,image(x(:,1:200)*70), shading interp;
fk1=[fk(1:n/2+1) fk(n/2+2:n)-fd];
kolf=exp(jk*2*pi*tau*fk1);
fo=zeros(1,n);
fo(kH-kl:kB+kl)= hann (kB-kH+2*kl+1); % вырезание полосы
Ro=repmat(fo,M,1); %Размножение матрицы
Per=1*n/2;%144%перекрытие
n_per=n-Per;
K=Per/2+1;

for i=1:100;
In=(i-1)*n_per+1;
Ik=In+n-1;
Y0=fft(x(:,In:Ik),n,2);
Y=Y0.*Ro;%вырезание полосы частот
z=sum(Y.*kolf,1); %Процедура формирования канала наблюдения
% сдвиг полосы частот
V=zeros(1,n);
V(k0:k0+kB-kH+2*kl)=z(kH-kl:kB+kl);
%Восстановление сигнала
U=ifft(z,n);
Ik1=i*n_per; In1=(i-1)*n_per+1; % изменить
w(In1:Ik1)=real(U(K:K+n_per-1));
U=ifft(V,n);
w1(In1:Ik1)=real(U(K:K+n_per-1));
end


nBCE=size(w,2); % число отсчетов в реализации
figure,plot(fd/nBCE*(0:nBCE-1),20*log10(abs(fft(w))));
xlabel('Гц')
ylabel('дБ')
figure, plot (w)
xlabel('T/dt')
sound (w,fd);
figure,plot(fd/nBCE*(0:nBCE-1),20*log10(abs(fft(w1))));
xlabel('Гц')
ylabel('дБ')
figure, plot (w1)
xlabel('T/dt')
sound (w1,fd);

figure,plot(abs(ifft(fo,512))),grid on;
figure,