Решеточное поглощение

4. Решеточное поглощение

Полупроводниковые соединения, состоящие из атомов различного типа, можно рассматривать как набор электрических диполей. Эти диполи могут поглощать энергию электромагнитного поля; наиболее сильное взаимодействие с излучением имеет место, если частота излучения равна частоте колебаний диполя. Это происходит в далекой инфракрасной области спектра. Обычно колебания являются сложными, включающими несколько типов нормальных колебаний (эмиссия многих фононов). Импульс фотона h/l пренебрежимо мал, тогда как фононы могут обладать квазиимпульсом вплоть до величины h/а (а — постоянная решетки).

Поэтому для выполнения закона сохранения квазиимпульса должны быть испущены два или более фононов. В полупроводниках имеются две поперечные оптические (ТО) ветви колебаний, две поперечные акустические (ТА), одна продольная оптическая (LO) и одна продольная акустическая (LA). Иногда две поперечные ветви колебаний обладают сходными кривыми дисперсии Е_р(k). Далее, некоторые комбинации фононов запрещены согласно правилам отбора. Тем не менее число возможных комбинаций всех этих типов колебаний чрезвычайно велико, и именно это обусловливает сложность обычно наблюдаемой структуры. На рисунке 4.1 показана часть спектра поглощения GaAs n-типа, связанного с колебаниями решетки [2].

В гомеополярных полупроводниках нет диполей. Однако спектры решеточного поглощения наблюдаются. Очевидно, имеет место процесс второго порядка: излучение индуцирует диполь, который сильно взаимодействует с излучением, и в результате возникают фононы. На рисунке 4.2 показан для примера спектр решеточного поглощения гомеополярного полупроводника Si, соответствующая идентификация фононов приведена в таблице 4.1. Для объяснения поглощения в области больших энергий привлекались процессы еще более высокого порядка, соответствующие одновременному испусканию четырех фононов [2].

Интересно отметить, что введение в гомеополярный полупроводник дефектов (например, путем облучения нейтронами) создает локальные поля, которые делают возможными однофононные переходы (в нормальных условиях запрещенные).

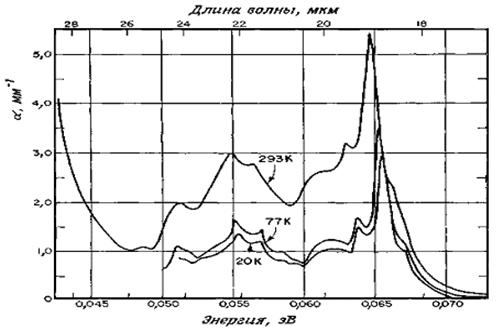
Рисунок 4.1. Спектр поглощения, связанного с колебаниями решетки, высокоомного GaAs n-типа в области энергий 0,04 — 0,07 эВ (нижняя шкала) при 20, 77 и 293 К.

Таблица 4.1. Фононы, участвующие в поглощении в кремнии

Волновое число, мм-1	Энергия пика, эВ	Тип фононов *
144,8	0,1795	3TO
137,8	0,1708	2TO + LO
130,2	0,1614	2TO + LO
		2TO + LA
96,4	0,1195	2ТО
89,6	0,1111	TO + LO
81,9	0,1015	TO + LA
74,0	0,0917	LO + LA
68,9	0,0756	ТО + ТА
61,0	0,0702	LO + TA

* ТО = 0, 0598 эВ, LO = 0 0513 эВ, LA = 0, 0414 эВ, ТА = 0, 0158 эВ.

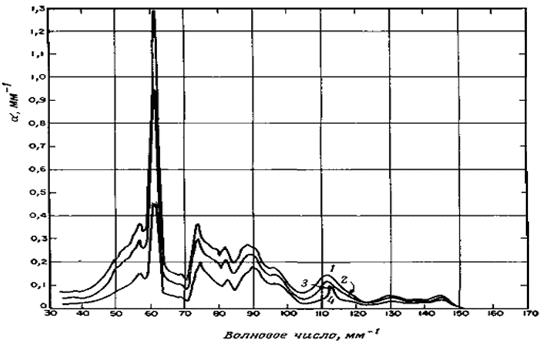
Рисунок 4.2. Решеточное поглощение в Si, выращенном в вакууме.

Кривая 1 — 365 К, кривая 2 — 290 К, кривая 3 — 77 К, кривая 4 — 20 К.

5. Методы определения коэффициента поглощения

Методы определения коэффициента поглощения можно разделить на несколько типов:

1.  Измерение коэффициента отражения и/или коэффициента отражения.

·  Если пленка не прозрачна (Т = 0), то выполняется равенство:

(5.1)

Следовательно, по данным измерений спектральной зависимости коэффициента отражения рассчитывается спектральная зависимость коэффициента поглощения [3].

·  Если пленка прозрачна, то равенство (5.1) преобразится в:

(5.2)

Таким образом из (5.2) следует, что по данным измерений спектральной зависимости коэффициентов отражения и пропускания можно рассчитать спектральную зависимость коэффициента поглощения.

2.  Расчеты по известным оптическим константам.

Оптические свойства веществ характеризуют, указывавшимся выше, комплексным показателем преломления. Зная его, можно вычислить коэффициент отражения любого материала. Один из методов рассчета описан Борном и Вольфом в [4].

3.  Прямые методы измерения коэффициента поглощения.

Например метод Табора и Стейнбергера [3]. На одной стороне образца находится исследуемая поверхность, а другая покрыта слоем с известным коэффициентом поглощения (например черной краской). Стороны попеременно подвергаются циклам облучения. Очевидно, что если подобрать подходящий температурный цикл, то тепловые потери скомпенсируются и можно будет определить отношение известного коэффициента поглощения к неизвестному.

6. Пример расчета спектральной зависимости коэффициента поглощения селективно поглощающего покрытия в видимой и ИК части спектра

Более полные теоретические выкладки с пояснениями вы можете найти в [4].

Зададим толщину мультипленки и количество пленок входящих в ее состав:

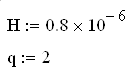
Определим комплексный показатель преломления (в мультипленке две пленки - q):

Определим характеристическую матрицу-функцию для одного слоя:

Введем характеристическую матрицу мультипленки, как произведение характеристических матриц пленок входящих в ее состав:

Энергетический коэффициент прозрачности будем вычислять по:

Энергетический коэффициент отражения будем вычислять по:

На рисунках 6.1, 6.2, 6.3 приведены рассчитанные программой MathCAD спектральные зависимости энергетических коэффициентов пропускания, отражения и поглощения.

Из этих рисунков видно, что чем тоньше мультиплека, тем более в коротковолновую часть спектра, в силу интерференции, сдвигается пересечение кривых спектральных зависимостей энергетических коэффициентов поглощения и отражения.

Можно заметить, что мультислой, спектральные зависимости энергетических коэффициентов которого представлены на рисунке 6.3, наиболее подходит для применения в качестве покрытий для тепловых коллекторов. При уменьшении толщины мультислоя и увеличении разницы в действительных частях комплексного коэффициента преломления можно достигнуть лучших спектральных зависимостей, т.е. больших значений коэффициента отражения в средней ИК части спектра и коэффициента поглощения в видимой области спектра.

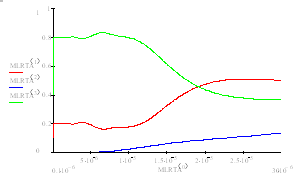
Рисунок 6.1 Рассчитанные спектральные зависимости энергетических коэффициентов поглощения (зеленая), пропускания (синяя) и отражения (красная) при N₁ = 2.0 + 1.0i N₂ = 4.0 + 1.5i d_{мультипленки} = 2 мкм.

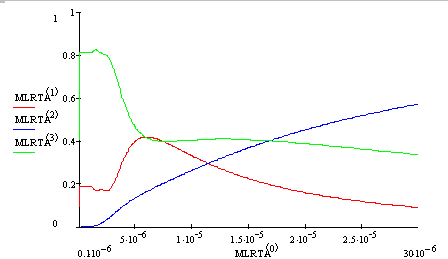
Рисунок 6.2 Рассчитанные спектральные зависимости энергетических коэффициентов поглощения (зеленая), пропускания (синяя) и отражения (красная) при N₁ = 1.8 + 1.0i N₂ = 3.0 + 1.0i d_{мультипленки} = 0.6 мкм.

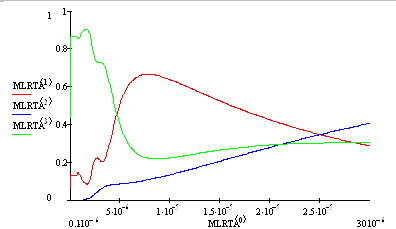
Рисунок 6.3 Рассчитанные спектральные зависимости энергетических коэффициентов поглощения (зеленая), пропускания (синяя) и отражения (красная) при N₁ = 1.6 + 0.8i N₂ = 5.0 + 1.0i d_{мультипленки} = 0.6 мкм.

Перечень ссылок

1.  В.Л. Бонч-Бруевич, С.Г. Калашников «Физика полупроводников», М.:«Наука», 1977.

2.  Ж. Панков «Оптические процессы в полупроводниках», перевод с англ. под ред. Ж.И. Алферова, М.:«Мир», 1973.

3.  Л.Ф. Друмметер, Г. Хасс «Поглощение солнечного излучения и тепловое излучение напыленных покрытий», в книге «Физика тонких пленок», том 2, перевод с англ. под ред. М.И. Елинсона, М.:«Мир», 1967.

4.  М. Борн, Э. Вольф «Основы оптики», перевод с англ. под ред. Г.П. Мотулевич, М.:«Наука», 1973.