Академия России
Кафедра Физики
Лекция
Переходные процессы в колебательных контурах
Орел 2009Содержание
Вступление
Переходные колебания в параллельном контуре
Свободные колебания в параллельном контуре
Режимы переходных колебаний в колебательных контурах
Переходные колебания при гармоническом воздействии
Литература
Вступление
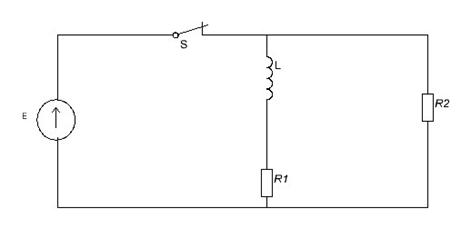
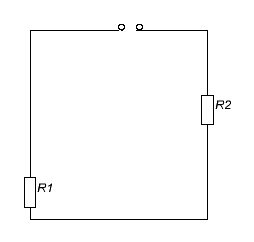
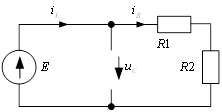
Колебательные контуры составляют значительную часть аппаратуры связи. Они могут выполнять самые различные функции: например, участвовать в выделении гармонических колебаний из последовательности видеоимпульсов, в формировании прямоугольных импульсов заданной длительности и др. На практике довольно распространен случай, когда на контур действует прямоугольный импульс (рис. 1).
 Рис. 1
Рис. 1 Если предположить ![]() , то нетрудно видеть, что при
, то нетрудно видеть, что при ![]() в контуре будет наблюдаться режим переходных колебаний, а с момента
в контуре будет наблюдаться режим переходных колебаний, а с момента ![]() – свободные колебания за счет запасенной реактивными элементами энергии. Рассмотрим оба этих случая на примере параллельного контура.
– свободные колебания за счет запасенной реактивными элементами энергии. Рассмотрим оба этих случая на примере параллельного контура.
Переходные колебания в параллельном контуре
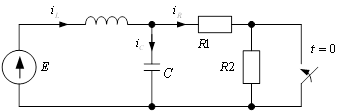
Пусть на параллельный контур, находящийся при ННУ, в момент ![]() действует перепад тока величиной
действует перепад тока величиной ![]() . Требуется определить реакцию – временную зависимость напряжения на контуре (рис. 2а).
. Требуется определить реакцию – временную зависимость напряжения на контуре (рис. 2а).
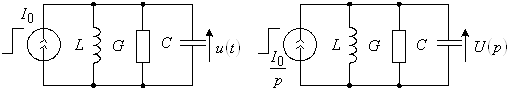
а) б)
Рис. 2
Для нахождения ![]() воспользуемся операторной схемой замещения, показанной на рис. 2,б. Найдем
воспользуемся операторной схемой замещения, показанной на рис. 2,б. Найдем ![]() :
:
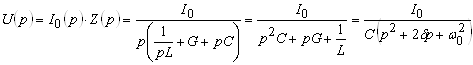
где ![]() – есть коэффициент затухания;
– есть коэффициент затухания;
![]() – частота собственных незатухающих колебаний.
– частота собственных незатухающих колебаний.
Воспользуемся таблицей соответствий (Л.0.1, стр. 222):
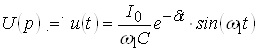 ,
,
где ![]() – частота собственных затухающих колебаний.
– частота собственных затухающих колебаний.
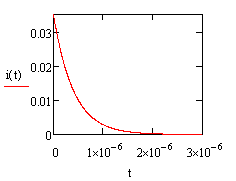
График имеет вид:

Рис. 3
Свободные колебания в параллельном контуре
Пусть в момент ![]() в схеме, показанной на рисунке 4а гасится источник тока
в схеме, показанной на рисунке 4а гасится источник тока ![]() . Требуется определить временную зависимость напряжения на контуре.
. Требуется определить временную зависимость напряжения на контуре.
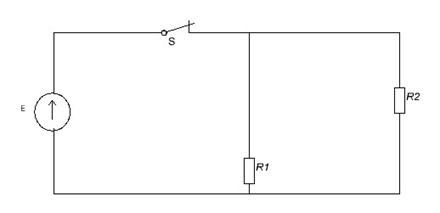
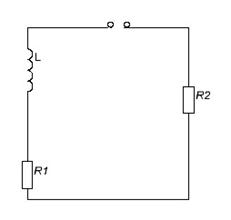
Примечание: Такая задача возникает после окончания действия прямоугольного импульса (рис. 1) на контур.
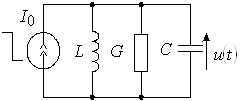
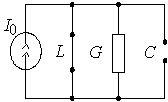
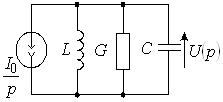
а) б) в)
Рис. 4
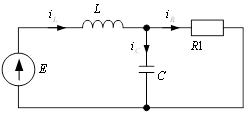
Для определения начальных условий изобразим эквивалентную схему (рис. 4б) для момента времени, непосредственно предшествующего коммутации. При этом для постоянного тока индуктивность представляется коротким замыканием, а емкость – обрывом цепи. Легко видеть, что до момента гашения весь ток источника будет проходить через индуктивность. Поэтому ![]() ,
, ![]() .
.
В операторной схеме (рис. 4б) индуктивность отображена схемой замещения с источником тока. Нахождение здесь ![]() отличается от предыдущего случая (рис. 2б) лишь направлением операторного источника тока. Следовательно, можно записать:
отличается от предыдущего случая (рис. 2б) лишь направлением операторного источника тока. Следовательно, можно записать:
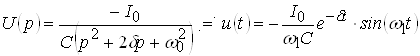 .
.
График данной зависимости будет зеркальным отображением зависимости (*), полученной для переходного процесса (рис. 5).
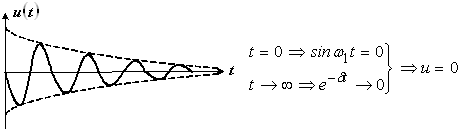
Рис. 5
Можно показать, что аналогичные результаты получаются при анализе переходных и свободных колебаний в последовательном контуре.
Отметим две особенности полученных выражений:
– во-первых, колебания носят гармонический характер, на что указывает множитель гармонической функции ![]() ;
;
– во-вторых, амплитуда полученных колебаний изменяется во времени по экспоненциальному закону ![]() .
.
Очевидно, что вид графиков найденных функций будет зависеть от величины коэффициента затухания ![]() и его соотношения с
и его соотношения с ![]() поскольку последним определяется величина
поскольку последним определяется величина ![]() .
.
Поэтому в зависимости от ![]() и
и ![]() различают несколько режимов колебаний. Рассмотрим их подробней применительно к параллельному контуру.
различают несколько режимов колебаний. Рассмотрим их подробней применительно к параллельному контуру.
Режимы переходных колебаний в колебательных контурах
Ранее было получено выражение для напряжения на контуре при ступенчатом воздействии:
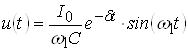 ,
,
где ![]() .
.
Для удобства изложения последующего материала выразим коэффициент затухания и частоту ![]() , через добротность:
, через добротность:
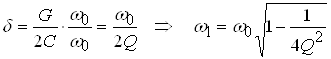 .
.
В зависимости от величины ![]() (или добротности
(или добротности ![]() ) будем различать четыре режима колебаний: колебательный, квазиколебательный, критический и апериодический.
) будем различать четыре режима колебаний: колебательный, квазиколебательный, критический и апериодический.
а) Колебательный режим.
Этот режим получается в контуре без потерь (идеальный контур), т. е. в чисто теоретическом случае: ![]()
![]() .
.
Выражение ![]() принимает вид:
принимает вид:
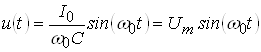 .
.
График полученного выражения показан на рисунке 6.

Рис. 6
б) Квазиколебательный режим.
Режим, который используется в подавляющем большинстве случаев.
Он получается при ![]()
![]() .
.
Для построения графика (рис. 7) используем выражение:
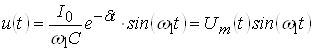 ,
,
где 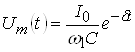 – амплитуда напряжения, убывающая по экспоненциальному закону.
– амплитуда напряжения, убывающая по экспоненциальному закону.
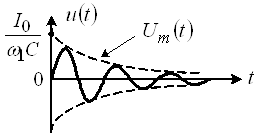
Рис. 7
Длительность переходных колебаний может быть найдена из условия, что амплитуда напряжения будет менее 5% от своего максимального значения, т. е.:
![]() , откуда
, откуда  .
.
Отсюда можно сделать вывод, что чем выше добротность контура ![]() (или чем меньше полоса пропускания
(или чем меньше полоса пропускания ![]() ), тем более длительным будет переходный процесс.
), тем более длительным будет переходный процесс.
Частота затухающих колебаний ![]() , однако это отличие незначительно. Действительно при средней добротности (
, однако это отличие незначительно. Действительно при средней добротности (![]() ), например
), например ![]() , имеем:
, имеем: 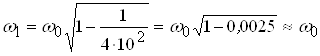 .
.
в) Критический режим.
Он возникает, когда ![]()
![]() .
.
В этом случае ![]() и получается неопределенность
и получается неопределенность ![]() .
.
Раскроем ее:
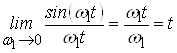 .
.
Выражение для ![]() принимает вид:
принимает вид:
![]() .
.
График этой функции начинается и заканчивается нулем, не пересекает ось времени. Исследуем его на экстремум:
![]() .
.
Экстремальные точки найдем из условия:
![]() ,
,
при этом:
![]() .
.
График напряжения в рассматриваемом режиме показан на рисунке 8.
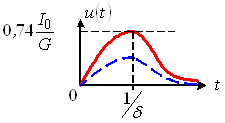
Рис. 8
г) Апериодический режим.
Такой режим получается при ![]() (
(![]() ), откуда следует, что
), откуда следует, что ![]() будет комплексной и не имеет физического смысла. График напряжения при этом будет менее выраженным, чем при критическом режиме (пунктир на рисунке 8).
будет комплексной и не имеет физического смысла. График напряжения при этом будет менее выраженным, чем при критическом режиме (пунктир на рисунке 8).
Вывод: изменяя добротность контура (например, с помощью шунтирующего сопротивления) можно изменять длительность и вид колебательного процесса.
Задание: Самостоятельно начертить график квазиколебательного процесса при воздействии на контур прямоугольного импульса.
Переходные колебания в параллельном контуре при гармоническом воздействии
Пусть на параллельный контур с резонансной частотой ![]() (рис. 9,а) находящийся при нулевых начальных условиях, в момент
(рис. 9,а) находящийся при нулевых начальных условиях, в момент ![]() действует гармоническое колебание, частота которого совпадает с
действует гармоническое колебание, частота которого совпадает с ![]() :
:
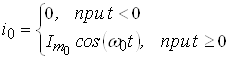 .
.
Требуется определить закон изменения напряжения на контуре.
Задачу решим в операторной форме, для чего перейдем к схеме замещения, показанной на рисунке 9,б.

а) б)
Рис. 9
По таблице соответствий воздействие ![]() имеет изображение:
имеет изображение:
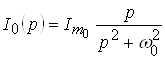 .
.
Определим операторную проводимость контура:
 ,
,
где ![]() и
и ![]() определены ранее.
определены ранее.
По закону Ома в операторной форме имеем:
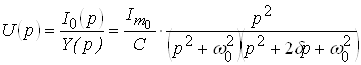 .
.
Поскольку в таблице соответствий нет нужной формулы для перехода во временную область, то данное выражение следует преобразовать.
Для этого воспользуемся теоремой разложения и методом неопределенных коэффициентов. Представим правильную дробь 4‑го порядка в виде суммы двух правильных дробей 2‑го порядка:
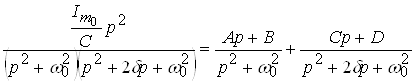 ,
,
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() — коэффициенты, подлежащие определению.
— коэффициенты, подлежащие определению.
Если данное выражение привести к общему знаменателю, раскрыть скобки в числителе и приравнять коэффициенты при одинаковых степенях ![]() , то получим систему 4‑х уравнений с 4‑мя неизвестными.
, то получим систему 4‑х уравнений с 4‑мя неизвестными.
Решая систему уравнений имеем: 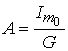 ;
; ![]() ;
; 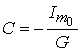 .
.
Теперь полученное выражение можно записать в виде:

и использовать таблицу соответствий.
По таблице соответствий находим оригинал:
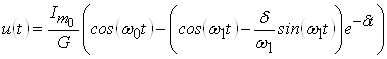 .
.
Предполагая, что контур имеет добротность, при которой ![]() ,
, 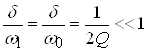 и, пренебрегая произведением
и, пренебрегая произведением 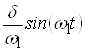 как очень малой величиной, получим:
как очень малой величиной, получим:
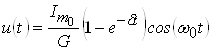 .
.
Из формулы следует, что процесс установления гармонического напряжения в контуре до амплитудного значения ![]() происходит не мгновенно, а за конечное время, определяемое множителем
происходит не мгновенно, а за конечное время, определяемое множителем ![]() .
.
Если процесс установления колебаний в контуре считать законченным при достижении напряжением величины более 95% от максимальной, то можно определить ![]() :
:
![]() ;
; ![]() .
.
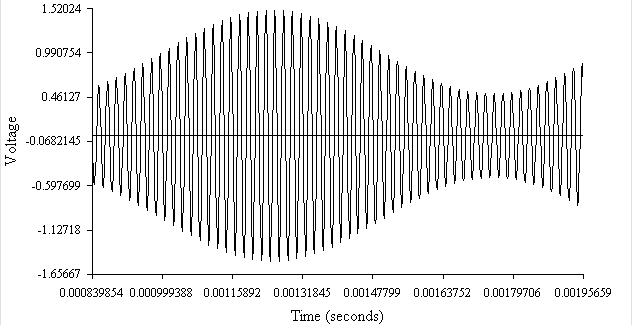
Видно, что время установления зависит от добротности контура: чем выше добротность, тем дольше происходят в контуре переходные процессы. На рисунке 10 показаны графики переходных колебаний при различных добротностях контура.
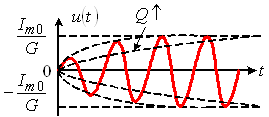 Рис. 10
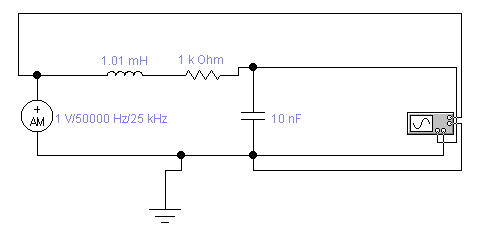
Рис. 10 В радиотехнических устройствах (например, в радиоприемниках) на параллельный контур обычно действуют гармонические колебания в виде радиоимпульсов с прямоугольной огибающей.
При этом чтобы напряжение на контуре достигло своего максимального значения, необходимо выполнять условие: 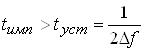 .
.
Отсюда, зная длительность радиоимпульсов, можно рассчитать минимальную полосу пропускания контура:
 , или его добротность:
, или его добротность: ![]() .
.
Литература
Белецкий А. Ф. Теория линейных электрических цепей. - М.: Радио и связь, 1986,
Шалашов Г. В. Переходные процессы в электрических цепях. – Орел: 1981
Похожие работы
... i(t) либо постоянная величина i0, либо синусоидальные токи in, то для их определения применяют известные методы расчета цепей постоянного и переменного синусоидального токов. Рассчитать формы и спектры сигналов при нелинейных преобразованиях Исходные данные: U0=0,5 В, U1=1 В, Um=1,5 В, S=16 мА/В, T=11 мкс 1. Рассчитаем угол отсечки θ в радианах и градусах cos θ= ...
... . В линейной цепи – это линейные дифференциальные уравнения (ЛДУ). Существуют различные методы решения таких уравнений, и соответственно различают различные методы расчета переходных процессов. 2 Способы получение характеристического уравнения Классический метод Классический метод основан на решении ЛДУ методом вариации произвольных постоянных. Любая система ЛДУ может быть сведена к одному ...
... увеличивается. Коэффициент модуляции mвых выходного АМ колебания через одиночный колебательный контур и систему связанных колебательных контуров уменьшается при увеличении модулирующей частоты. Перемодуляция АМ колебания возможна при коэффициенте модуляции большем единицы. Прохождение радиоимпульса через одиночный и систему связанных колебательных контуров Лабораторная работа по дисциплине ...
... регулировки усиления АРУ, а также специальные типы усилителей. Усилители имеющие логарифмическую зависимость выходного напряжения от входного называются логарифмическими. В настоящее время в приёмниках радиолокационных станций, предназначенных для обнаружения объектов применяются именно логарифмические усилители. Приёмники радиолокационных станций сопровождения объектов имеют АРУ. Частота ...
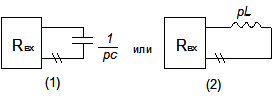
0 комментариев