Навигация
Муниципальное образовательное учреждение
«Средняя общеобразовательная школа № 24 с углубленным изучением предметов художественно-эстетического направления»
Школьная научно-практическая конференция
Реферат на тему: «Роль сил поверхностного натяжения в физике»
Выполнил:
Онохин Дмитрий Алексеевич, ученик 10 «А» класса,МОУ «СОШ № 24 с углубленным изучением предметов художественно-эстетического направления».
Научный руководитель:
Вольхин Николай Иванович,учитель физики,МОУ «СОШ № 24 с углубленным изучением предметов художественно-эстетического направления».
г. Архангельск, 2009
Оглавление
Введение
Метод пузырька
Метод проволочной
Метод капли
Опыт «Пробирка»
Опыт «Плато»
Роль поверхностного натяжения в жизни
Заключение
Библиография
Приложения
Введение.
Такие силы, как тяготение, упругость и трение, бросаются в глаза; мы ощущаем их непосредственно каждый день. Но в окружающем нас мире повседневных явлений действует еще одна сила, на которую мы обычно не обращаем никакого внимания. Сила эта сравнительно невелика, ее действия никогда не вызывают мощных эффектов. Она даже в последнее время исключена из программ приемных экзаменов для поступающих в вузы. Тем не менее мы не можем налить воды в стакан, вообще ничего не можем проделать с какой-либо жидкостью без того, чтобы не привести в действие силы, о которых у нас сейчас пойдет речь. Это силы поверхностного натяжения.
Сила поверхностного натяжения – это сила, обусловленная взаимным притяжением молекул жидкости, направленная по касательной к ее поверхности.
Действие сил поверхностного натяжения приводит к тому, что жидкость в равновесии имеет минимально возможную площадь поверхности. При контакте жидкости с другими телами жидкость имеет поверхность, соответствующую минимуму ее поверхностной энергии.
Понятие «поверхностное натяжение» впервые ввел Я. Сегнер (1752 год).
К вызываемым поверхностным натяжением эффектам мы настолько привыкли, что не замечаем их, если не развлекаемся пусканием мыльных пузырей. Однако в природе и нашей жизни они играют немалую роль.
Существует достаточно много различных методов определения поверхностного натяжения: метод капель, метод проволочной рамки, метод кольца, метод капиллярных волн, метод капли и пузырька и др. Метод проволочной рамки и метод кольца применяются для грубых измерений поверхностного натяжения.
1. Метод пузырька.
«Выдуйте мыльный пузырь и смотрите на него: вы можете заниматься всю жизнь его изучением, не переставая извлекать из него уроки физики», – писал великий английский физик лорд Кельвин.
В частности, мыльная пленка является прекрасным объектом для изучения поверхностного натяжения. Сила тяжести здесь практически роли не играет, так как мыльные пленки чрезвычайно тонки и их масса совершенно ничтожна. Поэтому основную роль играют силы поверхностного натяжения, благодаря которым форма пленки всегда оказывается такой, что ее площадь минимально возможная в данных условиях. Почему пленка обязательно мыльная? Все дело в структуре мыльной пленки. Мыло богато так называемыми поверхностно-активными веществами, концы длинных молекул которых по-разному относятся к воде: один конец охотно соединяется с молекулой воды, другой к воде безразличен. Поэтому мыльная пленка обладает сложной структурой: образующий ее мыльный раствор как бы «армирован» частоколом упорядоченно расположенных молекул поверхностно-активного вещества, входящего в состав мыла.
Вернемся к мыльным пузырям. Наверное, каждому доводилось не только наблюдать эти удивительно красивые творения, но и пускать их. Они сферичны по форме и долго могут свободно парить в воздухе. Давление внутри пузыря оказывается больше атмосферного. Избыточное давление обусловлено тем обстоятельством, что мыльная пленка, стремясь еще больше уменьшить свою поверхность, сдавливает воздух внутри пузыря, причем чем меньше его радиус, тем большим оказывается избыточное давление внутри пузыря.
Свободная поверхность жидкости стремится сократиться. Это можно наблюдать в случае, когда жидкость имеет форму тонкой пленки. Примером такого состояния могут служить мыльные пленки, подобные тем, которые вы получили в детстве, выдувая мыльные пузыри. Так как толщина мыльных пленок очень мала, жидкость в пленке можно рассматривать как два поверхностных слоя, не учитывая влияния молекул, находящихся между слоями. Получив мыльный пузырь от трубки, с помощью которой он был получен. Вы заметите, что пузырь уменьшается. Это свидетельствует о сокращении поверхности мыльной пленки.
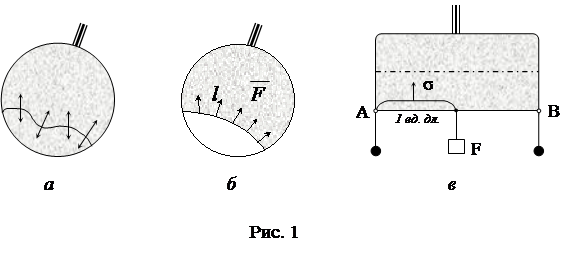
2. Метод проволочной рамки.
Возьмите проволочный четырехугольный каркас и соедините его противоположные вершины тонкой ненатянутой нитью. Опустив каркас в мыльную воду, вы заметите, что вытянутый из воды каркас затянут мыльной пленкой. Проколов пленку по одну сторону нити, вы увидите, что нить примет форму дуги. Опыт свидетельствует о том, что поверхность мыльной пленки сокращается.
Свойство поверхности жидкости сокращается можно истолковать как существование сил, стремящихся сократить эту поверхность. Эти силы называют силами поверхностного натяжения.
С помощью описанного ниже опыта можно найти способ измерения сил поверхностного натяжения. Если опустить в мыльную воду проволочный каркас, вынув его из воды, легко заметить, что верхняя часть каркаса (до упора) затянута мыльной пленкой. Если потянуть за подвижную сторону этой рамки вниз, то пленка растянется, а если подвижную сторону отпустить, то пленка сократится.
Пленка, образовавшаяся на рамке, представляет собой тонкий слой жидкости и имеет две свободные поверхности.
Поверхностное натяжение измеряется силой, с которой поверхностный слой действует на единицу длины того или иного контура на свободной поверхности жидкости по касательной к этой поверхности. В Международной системе единиц эта величина измеряется в ньютонах на метр (1 Н/м).
3. Метод капли.
Проще всего уловить характер сил поверхностного натяжения, наблюдая образование капли у плохо закрытого или неисправного крана. Пока капля мала, она не отрывается: ее удерживают силы поверхностного натяжения (поверхностный слой выполняет роль своеобразного мешочка). Чем больше капля, тем большую роль играет потенциальная энергия силы тяжести. Всмотритесь внимательно, как постепенно растет капля, образуется сужение – шейка, и капля отрывается.
Отрыв капли происходит в тот момент, когда ее вес становится равным равнодействующей сил поверхностного натяжения, действующих вдоль окружности шейки капли. Не нужно много фантазии, чтобы представить себе, что вода как бы заключена в эластичный мешочек, и этот мешочек разрывается, когда вес превысит его прочность.
В действительности, конечно, ничего, кроме воды, в капле нет, но сам поверхностный слой воды ведет себя как растянутая эластичная пленка.
А видели вы когда-нибудь очень большие капли?
В обычных условиях таких капель нет. И это не случайно – капли большого диаметра неустойчивы и разрываются на маленькие.
Похожие работы
... равновесия определяется конкурентной адсорбцией на поверхности растворенных компонентов. Связь поверхностного натяжения с адсорбцией Рассмотрим соотношение между адсорбцией и поверхностным натяжением в рамках теории регулярных растворов. Для обсуждения адсорбции растворенного вещества на поверхности жидкость-воздух необходимо определить, что такое поверхность. Первое определение поверхности ...
... , и начинаем отпускать его до момента образования плёнки. Отмечая новую тягу Р2, мы найдём для поверхностного натяжения s значение: . (8) §3. Определение коэффициента поверхностного натяжения методом компенсации давления Лапласа Молекулы жидкости взаимодействуют между собой силами притяжения и отталкивания, которые проявляются заметно в ...
... 0,428 0,2526 Расчеты по формуле (2) также предполагают 2 этапа исследований. На первом этапе определяется радиус пипетки по стандартному раствору, а на втором - измерение поверхностного натяжения исследуемой пробы. Расчеты по определению радиуса пипетки усложняется поправкой F, которая зависит от V/R3. Трудность состоит в том, что в формуле (2) радиус фигурирует в 2-х местах. Вычислять его ...
усаков, Н.М.Лубман, ЖФХ, 27, вып. 12, стр. 1887, 1953г. Следуя выводам авторов, можно утверждать, что поверхностное натяжение вычисляется следующим образом (см. рисунок): = d2 g /H, где d - диаметр пузырька; - плотность исследуемой среды; g - ускорение свободного падения; 1/H - параметр, зависящий от d/2h. Вычисляется с помощью таблицы. В сокращенном ...
0 комментариев