Навигация
Полый провод квадратного сечения
4. Полый провод квадратного сечения.
На низких частотах
![]() .
.
На высоких частотах
![]() ,
,
где l – длина провода; а – внешняя сторона контура поперечного сечения; t - толщина стенки (![]() ).
).
Система прямолинейных проводов:
1. Два параллельных провода (прямой и обратный):
а) для проводов круглого сечения одинакового диаметра на низких частотах
![]() .
.
На высоких частотах
![]() ,
,
где t – расстояние между осями проводов; d – диаметр провода; l – длина провода.
б) для одинаковых проводов прямоугольного сечения на низких частотах
L = 4*10-3![]() ,
,
где t – расстояние между центрами сечений; a и b – стороны сечения.
в) для проводов различных сечений
L = L1 + L2 – 2M,
где L1 и L2 – индуктивности каждого провода; М – взаимная индуктивность.
2. Проводник – земля. Индуктивность определяют по формулам параллельных проводов; значение ее вдвое меньше, чем вычисленное для системы прямого и обратного проводов при t = 2h (h – расстояние до поверхности земли).
Формулы справедливы при h »λ3 (λ3 – длина электромагнитных колебаний в земле).
Для приближенных расчетов
L = 2*10-3 l![]() .
.
3. Коаксиальный кабель:
L = 2*10-3 l![]() ,
,
где l – длина кабеля; D – внутренний диаметр наружного цилиндра; d – внешний диаметр внутреннего цилиндра; k – коэффициент, зависящий от частоты.
4. Пучок равноудаленных параллельных проводов (ориентировочно):
L=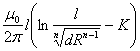 ,
,
где n – число проводов; d – диаметр отдельного провода; R – радиус размещения проводов (расстояние от центра пучка до центра любого провода);
K =![]() .
.
Значение К в зависимости от числа проводов n приведены в табл. 4
Табл. 4. Зависимость К от числа проводов n.
| n | 2 | 3 | 4 | 5 | 7 | 10 | 12 | 15 |
| K | 0,56 | 0,49 | 0,44 | 0,41 | 0,36 | 0,31 | 0,30 | 0,28 |
Конденсаторные секции.
1. Плоская конденсаторная секция:
![]() ,
,
где l – длина электрода; d – толщина диэлектрода; b – ширина диэлектрода.
Предполагается, что b»d»a (а – толщина электрода).
Если имеет место только неравенство d«b»a, то
![]() .
.
2. Плоская конденсаторная секция, состоящая из нескольких параллельно соединенных элементов:
![]() ,
,
где l – длина секции (в направлении между торцами обкладок); ![]() , где a и b – ширина и толщина секции.
, где a и b – ширина и толщина секции.
3. Цилиндрическая намотанная секция с выступающими обкладками (так называемая безындукционная намотка). Расчет индуктивности можно проводить по формуле для провода круглого сечения, принимая, что l – длина секции (в направлении между торцами обкладок), d – наружный диаметр секции.
Провод кругового сечения, изогнутый по дуге окружности:
![]() ,
,
где R – радиус окружности, по дуге которой изогнут провод; Ө - центральный угол, соответствующий длине провода; 0≤Ө≤2π; d – диаметр провода; k1 – коэффициент, которого на рис. 4; k2 = 1,02 для низких и средних частот; k2 = 0,77 для высоких частот.
В частном случае, когда
![]() «1,
«1,
![]()
Катушки индуктивности на замкнутых сердечниках
Сердечники тороидальной формы
1. Обмотка на каркасе. При массивных измерениях магнитных параметров сердечников иногда используют разъемные обмотки, вмонтированные в каркас прямоугольного сечения, внутрь которого помещают тороидальные сердечники (табл. 5.).
Табл. 5. Расчет индуктивности катушек на сердечниках тороидальной формы.
| Вариант геометрии сечения | |
| Приближенные формулы | |
|
|
|
| Уточненные формулы | |
|
|
|
| Отношение величин h, вычисленных по приближенным формулам, к величинам, вычисленным по уточненным формулам. | |
Связь между магнитной проницаемостью материала сердечника μrи индуктивностью катушки L в этом случае устанавливает формула
![]() ,
,
где S и SК – площади поперечных сечений сердечников и каркаса;
![]() ,
,
где DK и dK – наружный и внутренний диаметры каркаса.
3. Неполная обмотка (рис. 4.).
 ;
;
![]() ;
;
где S – сечение магнитопровода; lср – длина средней линии магнитопровода; pср – периметр среднего витка.
Катушки индуктивности на разомкнутых сердечниках
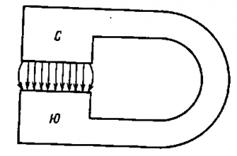
Катушки на сердечниках с малыми зазорами.
Приведенные формулы справедливы при условии δ « а, где δ – ширина зазора; а – любой линейный размер поперечного сечения магнитопровода:
![]() ; μr > 1;
; μr > 1;
![]() ;μr » 1;
;μr » 1;
![]() ; μr→ ∞,
; μr→ ∞,
где N – коэффициент размагничивания.
Сердечники с большими воздушными зазорами.
Формулы для случая малых зазоров были выведены в предположении, что поле в зазоре близко к однородному и величина потоков рассеяния пренебрежимо мала по сравнению с рабочим потоком. Если же магнитопровод содержит воздушный зазор, для которого не выполняется условие δ « а, то с целью сохранения формы записи соотношений для расчета магнитной цепи, справедливых при малых зазорах, целесообразно ввести понятие об эквивалентном зазоре.
Наиболее удобным, оказалось, определить эквивалентный зазор как такой, который имеет ту же проводимость, что и реальный; а геометрия его определяется сечением полюсов магнитопровода и некоторой эквивалентной длиной δЭ. при этом все формулы для сердечников с зазором остаются справедливыми при подстановке в них δЭ вместо δ.
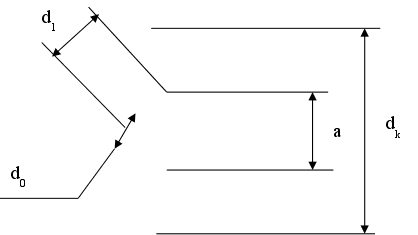
На практике часто встречаются полюса магнитопровода в виде двух прямоугольных призм, расположенных друг против друга. Выражение для δЭ в этом случае имеет вид
![]()
(обмотка не перекрывает зазора) или
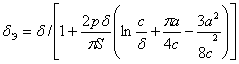
(обмотка перекрывает зазор), где δ – геометрическая длина зазора; p – периметр сечения магнитопровода у зазора; S – сечение магнитопровода у зазора (т. е. сечение полюса); 2с – высота обмотки; а – расстояние от сердечника до средней линии продольного сечения обмотки (т. е. приближенно полуширина обмотки).
Катушки индуктивности с немагнитными сердечниками
Немагнитные сердечники в катушках индуктивности используются в качестве элементов подстройки при работе в области высоких частот. Влияние таких сердечников на параметры катушек аналогично влиянию экрана, т.е. приводит к уменьшению индуктивности и добротности и к увеличению вносимого сопротивления и емкости.
Экран и немагнитный сердечник могут в известном приближении рассматриваться как короткозамкнутый виток, индуктивно связанный с катушкой.
Потери в катушках индуктивности. Добротность
Определение потерь в катушках индуктивности является существенны, главным образом, с точки зрения их влияния их (потерь) на характеристики схемы, в которую катушки входят. Значительно реже вычисление потерь представляет интерес с точки зрения мощности, дополнительно затрачиваемой источником питания (или источником сигнала); эта мощность может, кроме того, привести к нежелательному изменению теплового режима элементов.
Общая формула для добротности имеет вид
![]() ,
,
где Rэ – эквивалентное сопротивление, учитывающее потери в катушке (в обмотке и сердечнике).
В связи с тем, что катушки обладают собственной емкостью, существует некоторая частота ƒ0 (собственная, или резонансная), вблизи которой емкость оказывает существенное влияние на добротность (из-за изменений действующих индуктивности и сопротивления).
Влияние собственной емкости на добротность катушки описывается формулой
∆Q = -Q (ƒ / ƒ0)2,
где ∆Q – уменьшение добротности Q при работе на частоте ƒ < ƒ0.
Из-за приближенного характера формул для определения ƒ0 и для учета его влияния на добротность практически величиной ∆Q можно пренебречь уже при ƒ ≤ ƒ0 / 3.
Потери в катушках складываются из следующих составляющих: потери в проводе; диэлектрические потери в каркасе и изоляции провода; потери в сердечнике.
Похожие работы
... конструкции и технологии изготовления таких изделий. 1. АНАЛИЗ ТЕХНИЧЕСКОГО ЗАДАНИЯ Согласно технического задания необходимо спроектировать экранированную катушку индуктивности : Рабочая частота – 5 МГц L = 20 мкГн Для обеспечения стабильности катушки индуктивности в указанных условиях эксплуатации, а именно: В 3.1 по ГОСТ 15150-69, всеклиматическое исполнение подразумевает рабочий ...
... электромагнитные свойства и стабильность, превосходящие существующие, а также развитием конструкции и технологии изготовления этих изделий. В данном курсовом проекте будем проектировать экранированную катушку индуктивности. 1. Анализ технического задания Заданием данного курсового проекта является проектирование экранированной катушки фильтра промежуточной частоты (ФПЧ) диапазона УКВ бытового ...
... , гидравлических системах и проч. Соленоиды на переменном токе применяются в качестве индуктора для индукционного нагрева в индукционных тигельных печах.4. Расчет намагничивающего устройства для магнитопорошкового метода неразрушающего контроля Исходные данные для расчета: 1 Соленоид круглого сечения диаметром 30 мм и длиной 200 мм; 2 Материал сердечника – Сталь 20; 3 Провод обмотки ...
... при t=+200C; - температурный коэффициент затухания; t - заданная температура. Температурный коэффициент имеет сложную зависимость от частоты, а также от конструкции кабеля. Поэтому при расчетах пользуются экспериментальными значениями , которые приведены в таблице. f,кГц R,Ом/км G, Сим/км*10-7 ,Неп/км *10-3 , Неп/км 10 68.4 6.28 0.21 2.7 ...

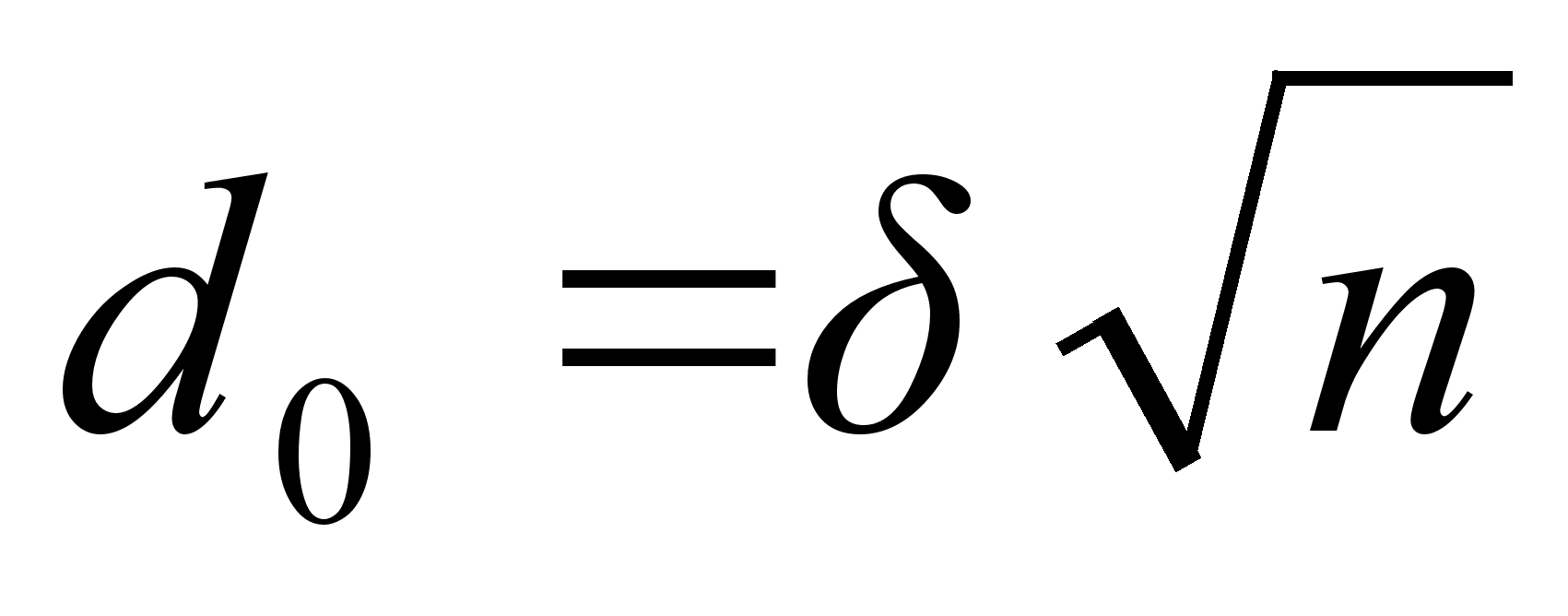
0 комментариев