Министерство Образования Российской Федерации
Омский государственный технический университет
Кафедра “Авиа- и ракетостроение”
Расчетно-графическая работа
Расчет сверхзвукового обтекания заостренных тел вращения
КР 2068998-00.00.00.000.ПЗ
Омск 2006
Введение
Некоторые летательные аппараты (например, ракета, артиллерийский снаряд) или их конструктивные элементы могут иметь форму тела вращения. Исследования обтекания таких тел составляют содержание одного из важнейших разделов современной аэродинамики.
Корпус (фюзеляж) в виде тела вращения, или тела, по форме близкого к нему, представляет собой наряду с крыльями, управляющими и стабилизирующими элементами важнейшую часть многих летательных аппаратов. Некоторые типы аппаратов имеют корпус, как единственный, другие - как основной элемент аэродинамической схемы. Поэтому, в аэродинамических исследованиях изучение обтекания тел вращения и разработка методов расчета силового воздействия на них при таком обтекании занимают большое место.
Результаты аэродинамического расчета можно использовать для оценки аэродинамических свойств летательного аппарата, если он собой по форме представляет тело вращения, или же применить эти результаты с соответствующими данными для несущих поверхностей (крыльев, рулей, стабилизаторов) и интерференционными поправками как отдельные составляющие для комбинации «корпус- крыло- оперение».
Расчет установившегося обтекания летательных аппаратов, имеющих форму тонкого заостренного тела вращения, можно производить путем линеаризации задачи. Соответствующие способы расчета, основанные на методе источников и диполей. Дают возможность определить параметры потока на поверхности тонкого заостренного тела вращения, а также, его аэродинамические коэффициенты, как при осесимметричном обтекании, так и при движении под малым углом атаки.
Задание
Найти распределение диполей (функцию m(ε)) на цилиндрическом корпусе, имеющем заостренную головную часть с параболической образующей. Корпус совершает движение при M¥, под некоторым углом атаки α и одновременно вращается с угловой скоростью ![]() вокруг поперечной оси, проходящей через центр масс. Длина тела xk, длина головной части xмид, расстояние от носка до центра масс хм, радиус корпуса rмид.
вокруг поперечной оси, проходящей через центр масс. Длина тела xk, длина головной части xмид, расстояние от носка до центра масс хм, радиус корпуса rмид.
Исходные данные для расчета:
M¥=1.5; xk=7.5 м; xмид=4.5; хм=5; rмид=1.5.
Корпус разбиваем на n=15 частей.
Расчет первых трех точек в MathCAD:
![]()
![]()
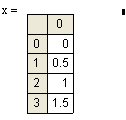
Формула для расчета радиуса тела:


![]()
Интенсивность диполей при обтекании под нулевым углом атаки рассчитывается по формулам:
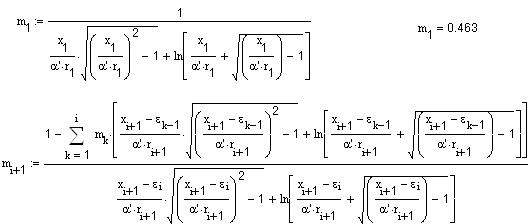
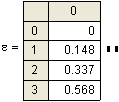
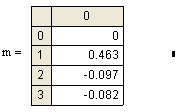
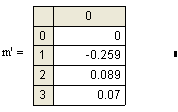
Распределение диполей первых трех точек:
Коэффициент давления при обтекании под нулевым углом атаки расчитывается по формуле:
 .
. 
Интенсивность диполей при обтекании под малым углом атаки рассчитывается по формулам:

Расчет коэффициента давления при обтекании под малым углом атаки


Текст программы расчета выполненной в среде Delphi:
unit Unit1;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, Grids, StdCtrls, ExtCtrls, ComCtrls, TeEngine, Series, TeeProcs,
Chart, Buttons, DbChart, math, Menus;
type
TForm1 = class(TForm)
PageControl1: TPageControl;
TabSheet1: TTabSheet;
TabSheet2: TTabSheet;
PageControl2: TPageControl;
TabSheet3: TTabSheet;
TabSheet4: TTabSheet;
TabSheet5: TTabSheet;
TabSheet6: TTabSheet;
TabSheet7: TTabSheet;
LabeledEdit1: TLabeledEdit;
LabeledEdit2: TLabeledEdit;
LabeledEdit3: TLabeledEdit;
LabeledEdit4: TLabeledEdit;
LabeledEdit5: TLabeledEdit;
LabeledEdit6: TLabeledEdit;
Panel1: TPanel;
Button1: TButton;
StringGrid1: TStringGrid;
Chart1: TChart;
Chart2: TChart;
Chart3: TChart;
Chart4: TChart;
Chart5: TChart;
Series1: TLineSeries;
Series2: TLineSeries;
Series3: TLineSeries;
Series4: TLineSeries;
Series5: TLineSeries;
procedure FormCreate(Sender: TObject);
procedure Button1Click(Sender: TObject);
type
vector = array[0..101]of real;
var
Form1: TForm1;
n:integer;
m,p,m1,p1:Vector;
x,r,e:vector;
implementation
procedure DoCount(const Minf,Xk,Xmid,Xm,Rmid:real);
var a1,pr,sm:real;
k,i:Integer;
begin
a1:= sqrt( sqr(Minf)-1);
x[0]:=0;
for i := 1 to n do
x[i]:=x[i-1]+Xk/n;
for i:=0 to n do
if x[i]<=Xmid then r[i]:= (Rmid/Xmid)*(2-x[i]/Xmid)*x[i]
else r[i]:= Rmid ;
for i := 1 to n do
begin
e[i]:=x[i]-a1*r[i];
end;
pr:=x[1]/(a1*r[1]);
m[1]:= 1/(pr*sqrt(pr*pr-1)+ln(pr+sqrt(pr-1)));
for i := 1 to n-1 do
begin
sm:=0;
pr:=0;
for k := 1 to i do
begin
pr:=(x[i+1]-e[k-1])/(a1*r[i+1]);
sm:=sm+ m[k]*( pr* sqrt(pr*pr - 1)+ln( pr + sqrt(pr-1) ))
end;
pr:=(x[i+1]-e[i])/(a1*r[i+1]);
m[i+1]:=(1-sm)/( pr* sqrt(pr*pr-1)+ln( pr + sqrt(pr-1) ));
end;
for i:= 1 to n-1 do
begin
sm:=0;
for k:=1 to i do
begin
pr:=(x[i]-e[k-1])/(a1*r[i]);
sm:= sm+ m[i]*sqrt( pr*pr-1)
end;
p[i]:=(-4/a1)*sm;
end;
pr:=(x[1])/(a1*r[1]);
m1[1]:=((x[1]-Xm)/Xk)/(pr*sqrt(pr*pr-1)+arccosh(pr));
for i := 1 to n-1 do
begin
sm:=0;
for k := 1 to i do
begin
pr:=(x[i+1]-e[k-1])/(a1*r[i+1]);
sm:=sm+m1[k]*(pr*sqrt(pr*pr-1)+arccosh(pr))
end;
pr:=(x[i+1]-e[i])/(a1*r[i+1]);
m1[i+1]:=( ( (x[i+1]-Xm)/Xk )-sm)/
(pr*sqrt(pr*pr-1)+arccosh(pr));
end;
for i:= 1 to n-1 do
begin
sm:=0;
for k:=1 to i do
begin
pr:=(x[i]-e[k-1])/(a1*r[i]);
sm:= sm+ m1[k]*sqrt( pr*pr-1)
end;
p1[i]:=(-4/a1)*sm;
end;
end;
procedure TForm1.FormCreate(Sender: TObject);
begin
n:=StrToInt(LabeledEdit6.Text);
DecimalSeparator:='.';
StringGrid1.Cells[0,0]:= '№';
StringGrid1.Cells[1,0]:= 'X';
StringGrid1.Cells[2,0]:= 'R';
StringGrid1.Cells[3,0]:= 'm';
StringGrid1.Cells[4,0]:= 'p';
StringGrid1.Cells[5,0]:= 'm1';
StringGrid1.Cells[6,0]:= 'p1';
end;
procedure TForm1.Button1Click(Sender: TObject);
var i:integer;
begin
n:=StrToInt(LabeledEdit6.Text);
StringGrid1.RowCount:=n+1;
for i := 1 to n+1 do
with StringGrid1 do
begin
Cells[0,i]:= IntToStr(i-1);
end;
try
DoCount (StrToFloat(LabeledEdit1.Text),
StrToFloat(LabeledEdit2.Text),
StrToFloat(LabeledEdit3.Text),
StrToFloat(LabeledEdit4.Text),
StrToFloat(LabeledEdit5.Text));
except
ShowMessage('Проверьте введенные параметры!');
end;
Series1.Clear;
Series2.Clear;
Series3.Clear;
Series4.Clear;
Series5.Clear;
for i:= 0 to n do
begin
try
//рисую графики
Series1.Add(r[i]);
Series2.Add(m[i]);
Series3.Add(p[i]);
Series4.Add(m1[i]);
Series5.Add(p1[i]);
//Заполняю таблицу
StringGrid1.Cells[1,i+1]:= FloatToStrF(x[i],ffFixed,3,3);
StringGrid1.Cells[2,i+1]:= FloatToStrF(r[i],ffFixed,3,3);
StringGrid1.Cells[3,i+1]:= FloatToStrF(m[i],ffFixed,3,3);
StringGrid1.Cells[4,i+1]:= FloatToStrF(p[i],ffFixed,3,3);
StringGrid1.Cells[5,i+1]:= FloatToStrF(m1[i],ffFixed,3,3);
StringGrid1.Cells[6,i+1]:= FloatToStrF(p1[i],ffFixed,3,3);
except
end;
end;
end;
end.
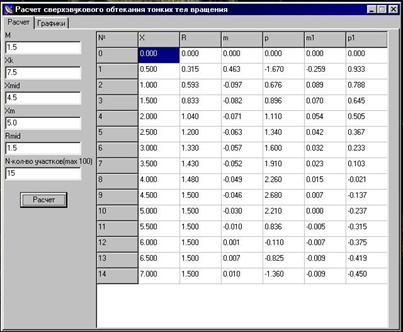
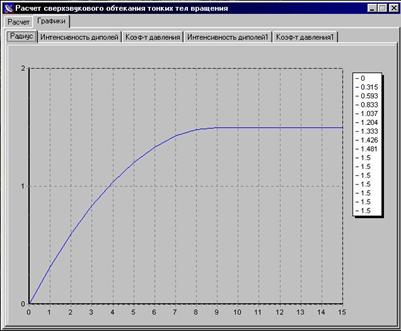
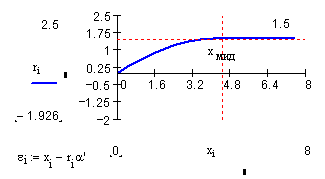
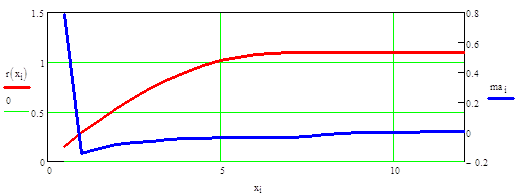
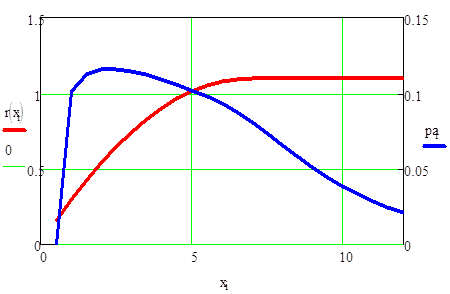
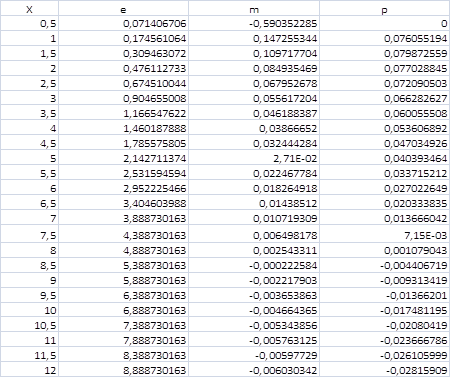
Скришоты работы программы в сравнении с графиками MathCad:
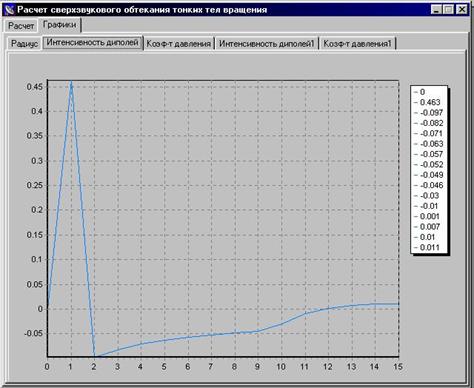
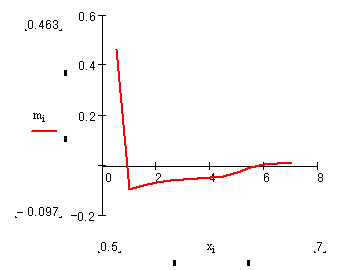
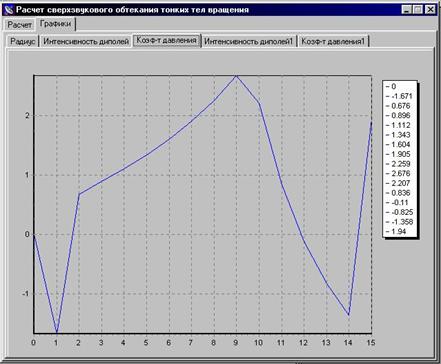
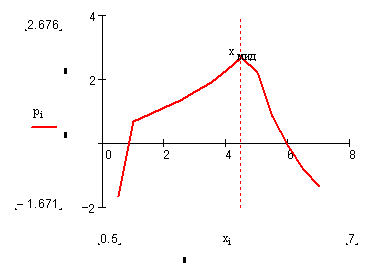
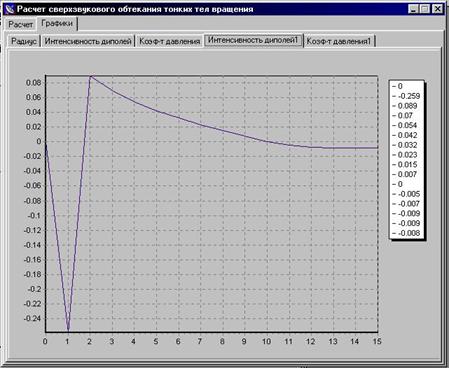
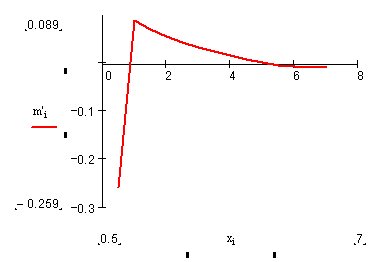
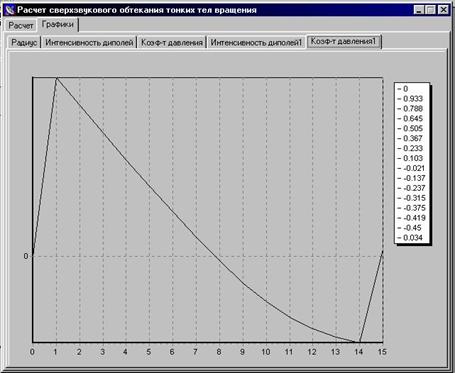
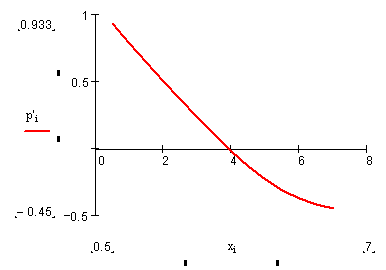
Вывод
Проведенный в программе расчет на первых трех участках совпадает с данными, полученными при моделировании в MathCAD (с точностью до 103), поэтому принимается, что программа расчета дает справедливые результаты для остальных участков обтекаемого тела.
Список литературы
1. Кузнецов В.И., Макаров В.В. Сверхзвуковое обтекание заостренных тел вращения: Учебное пособие.- Омск: Изд-во ОмГТУ, 1999г.- 80с.
2. Кузнецов В.И., Макаров В.В. Аэрогазодинамика в вопросах и задачах: практикум.- Омск: Изд-во ОмГТУ, 2002г.- 80с.
Похожие работы
... безотрывного обтекания . (2.17) Суммируя для всех , получаем . Используя условие безотрывного обтекания, можно вычислить производную , определяющую интенсивность диполей. В соответствии с этим условием Выберем на образующей заданного тела вращения достаточно густой ряд точек и определим координаты точек, лежащие на пересечении с осью соответствующих линий Маха Рассмотрим точку ...
... обтекании самой модели, поэтому для компенсации этих потерь сверхзвуковые А. т. имеют многоступенчатые компрессоры и более мощные силовые установки, чем дозвуковые А. т. 3.3. Аэродинамические трубы для болидов Формулы 1. Для нужд автомобильной промышленности в основном используются дозвуковые АТ замкнутого (геттингенского) типа с обратным воздушным потоком. Такие трубы благодаря замкнутому ...
... ) при запуске в серийное производство контейнеров с оборудованием. Все это ведет к снижению сроков и затрат на подготовку производства. 5Автоматизированное проектирование деталей крыла В настоящем разделе проекта рассматривается автоматизированное проектирование деталей и узлов с целью увязки конструкции и подготовки информации для изготовления шаблонов, технологической оснастки и самих деталей. ...
... состояние равновесия – на поверхность тела действует сила давления жидкости, которая уравновешивает вес жидкости внутри поверхности. Движение жидкостей и газов. Движение жидкостей и газов, как и все другие виды движения, рассматриваемые в механике, можно полностью охарактеризовать, оперируя единицами измерения длины, времени и силы. Так, диаметр парашюта можно измерять в метрах, время ...
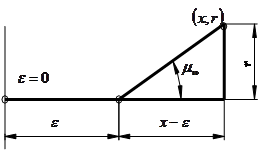






0 комментариев