Механика жидкости и газа

Содержание.

Введение. 2

Гидроаэромеханика. 3

Законы механики сплошной среды. 4

Закон сохранения импульса. 5

Закон сохранения момента импульса. 5

Закон сохранения энергии. 6

Гидростатика. Равновесие жидкостей и газов. 9

Движение жидкостей и газов. 10

Прогнозирование характеристик течения. 10

Уравнение неразрывности. 11

Уравнение Бернулли. 11

Гравитационное моделирование. 13

Число Фруда. 13

Гидродинамика Эйлера и Навье-Стокса. 14

Влияние вязкости на картину течения. 15

Турбулентное течение в трубах. 16

Гидравлический удар. 17

Явления в пограничном слое. 18

Вихревые колебания. 19

Плоская поверхность. 20

Поверхности другой формы. 21

Сжимаемость. 21

Аналогии между течением жидкости и газа. 23

Заключение. 24

Список использованной литературы. 27

Введение.

Как манна небесная свалилось на учёных-физиков XIX века совпадение положений кинетической теории газов с экспериментальными результатами, полученными в рамках термодинамики. Два физических подхода – макроскопический (термодинамический) и микроскопический (молекулярно-кинетический) – дополнили друг друга. Идея о том, что вещество состоит из молекул, а те, в свою очередь, из атомов нашла убедительное подтверждение.

Казалось, на основе кинетической теории, легко можно определить свойства газов, поскольку достаточно знать свойства входящих в состав молекулы атомов для определения свойств самого вещества, но в действительности всё оказалось не так просто. Благодаря этой теории удалось определить лишь некоторые свойства газов, например, вывести уравнение состояния газа, но для определения таких характеристик газов как коэффициенты теплопроводности, вязкости и диффузии нужно было серьёзно потрудиться. Для конденсированных сред - твёрдых тел, жидкостей и сжатых газов получить результаты было ещё труднее, поскольку должно учитываться то, что молекулы взаимодействуют между собой не только при ударах. Поэтому, говорить о том, что все физические явления микромира могут быть объяснены и рассчитаны на основе молекулярно-кинетических представлений, не приходиться.

Дискретное (не сплошное) строение вещества было обнаружено лишь в конце XIX века, а опыты, доказывающие существование молекул, проведены в 1908 году французским физиком Жаном Батистом Перреном. Обнаружение дискретной структуры строения вещества позволило определить границы применимости механики сплошных сред. Она работает только в тех случаях, когда систему можно разбить на малые объёмы, в каждом из которых содержиться всё же достаточно большое количество частиц, чтобы оно подчинялось статистическим закономерностям. Тогда элементы среды находятся в состоянии термодинамического равновесия, а их свойства описываются небольшим числом макроскопических параметров. Изменения в таком малом объёме должны происходить достаточно медленно, чтобы термодинамическое равновесие сохранялось.

При выполнении этих условий, справедлива гипотеза о сплошности среды, которая лежит в основе механики сплошной среды. Сплошной средой считается не только твёрдое тело, жидкость или газ, но и плазма (даже сильно разряженная), такая, как звёздный ветер. Число частиц в элементе объёма такой среды невелико, но благодаря большому радиусу действия сил между заряженными частицами микроскопические параметры меняются от элемента к элементу непрерывно.

Как движется в вакууме материальная точка досконально известно со времён Исаака Ньютона. Гораздо сложнее описать её движение в воздухе, воде или другой среде. Именно с этими вопросами имеет дело, являющаяся разделом физики, наука гидроаэромеханика.

Гидроаэромеханика.

Несмотря на то, что газ и жидкость – разные фазовые состояния вещества, гидроаэромеханика (механика текучих веществ), в изучении этих фаз вещества, не разделяет их, а изучает их механические свойства, взаимодействие этих свойств между собой и с граничащими с ними твёрдыми телами. Гидроаэромеханика состоит из нескольких разделов:

1.  движение со скоростью, много меньшей скорости звука, изучает гидродинамика.

2.  Если скорость движения тела приблизительно равна скорости звука или превышает оную, такое движение исследует газовая динамика.

3.  изучение движения тел и летательных аппаратов в атмосфере относиться к разделу аэромеханики.

Объединяющими все разделы гидроаэромеханики цели – улучшить форму летательных аппаратов, автомобилей; добиться наибольшей эффективности устройств, использующих жидкость или газ (двигателей реактивных самолётов или впрыскивателей топлива в двигателях внутреннего сгорания); оптимизировать производственные процессы, связанные с использованием жидкости или газа (аэрозольное нанесение покрытий, создание оптических волокон, т. д.). Гидроаэромеханика отличается как от эмпирической гидравлики, так и от математической гидродинамики, поскольку она не только основывается на твердо установленных законах физики, но и опирается на опытные данные, проверяя и дополняя ими теоретический анализ. Законы гидроаэромеханики оказываются полезными не только в технике и промышленности – они помогают предсказать и объяснить многие природные явления, связанные с динамическими свойствами воздуха и воды. Гидроаэромеханика работает фактически во всех отраслях деятельности человека.

Законы механики сплошной среды.

Механика сплошной среды основывается на трёх главных законах:

1.  Сохранение массы (сохранение импульса)

2.  Сохранение энергии

3.  Второй закон Ньютона (изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует).

Но, в отличие от механики материальной точки, в законе сохранения энергии учитывается помимо потенциальной и кинетической ещё и внутренняя энергия, а в законе изменения импульса кроме «обычных» объёмных сил – тяжести, электромагнитных и инерционных – на вещество действуют дополнительно и поверхностные силы (поверхностные напряжения). В случае гидроаэромеханики примером поверхностной силы является давление – нормальное напряжение.

Давление p в газе и жидкости создаётся за счёт хаотических столкновений молекул и связано с другими параметрами состояния вещества, например, температурой Т и плотностью р – уравнением состояния. Для идеального газа таким уравнением состояния является уравнение Клапейрона – Менделеева:

Р = рRT

M

где R – газовая постоянная, М – молярная масса.

Для жидкости, учитывая её малую сжимаемость, вместо этого соотношения обычно используется условие несжимаемости, которое существенно упрощает уравнение аэромеханики:

p = const.

Внутренняя энергия u также определяется уравнением состояния. В небольшом диапазоне температур можно считать, что внутренняя энергия 1 моля вещества линейно зависит от температуры:

U = c_vT

Где c_v – молярная теплоёмкость вещества при постоянном объёме.

Закон сохранения импульса.

Из законов Ньютона можно показать, что при движении в пустом пространстве импульс сохраняется во времени, а при наличии взаимодействия скорость его изменения определяется суммой приложенных сил. В классической механике закон сохранения импульса обычно выводится как следствие законов Ньютона. Однако, этот закон сохранения верен и в случаях, когда Ньютоновская механика неприменима (релятивистская физика, квантовая механика). Как отмечалось, он может быть получен как следствие интуитивно-верного утверждения о том, что свойства нашего мира не изменятся, если все его объекты (или начало отсчета!) переместить на некоторый вектор L. В настоящее время не существует каких-либо экспериментальных фактов, свидетельствующих о невыполнении закона сохранения импульса.

Закон сохранения момента импульса.

Если понятие импульса в классической механике характеризует поступательное движение тел, момент импульса вводится для характеристики вращения и является следствием утверждения о том, что свойства окружающего мира не изменяются при поворотах (или повороте системы отсчета) в пространстве.

В случае неравенства нулю момента силы наблюдается весьма "необычное" с точки зрения "здравого смысла" поведение быстро вращающихся тел (их момент импульса направлен по оси вращения) с помещенной на острие осью вращения. Такие тела под действием внешних сил (например, силы тяжести) вместо того, чтобы перемещаться в сторону действия силы, начинают медленно вращаться вокруг острия в перпендикулярной приложенной силе плоскости. Несмотря на то, что подобное поведение является непосредственным следствием законов Ньютона (или еще более общих законов сохранения и симметрии), этот эффект часто не только вызывает удивление у лиц, мало знакомых с точными науками, но и дает им повод рассуждать об "ошибочности современного естествознания вообще и классической физики в частности. Основанный на принципе "...если я не понимаю теории или наблюдаемого эффекта, то тем хуже для них...", к сожалению до сих пор все еще популярен, хотя уже на протяжении нескольких столетий развивающееся естествознание демонстрирует его весьма низкую эвристическую эффективность.

Закон сохранения энергии.

Первоначально в механике были введены кинетическая энергия (обусловленная движением тела) и потенциальная (обусловленная взаимодействиями между телами и зависящая от их расположения в пространстве). Конкретное математическое выражение для потенциальной энергии определяется взаимодействиями между объектами. В большинстве механических систем механическая энергия (сумма кинетической и потенциальной) сохраняется во времени (например в случае мяча, упруго ударяющегося о пол). Однако нередки и такие системы, в которых механическая энергия изменяется (чаще всего убывает). Для описания этого были введены диссипативные силы (например силы вязкого и сухого трения и др.). Со временем выяснилось, что диссипативные силы описывают не исчезновение или возникновение механической энергии, а переходы ее в другие формы (тепловую, электромагнитную, энергию связи и т.д.). История развития естествознания знает несколько примеров того, как кажущееся нарушение закона сохранения энергии стимулировало поиск ранее неизвестных каналов ее преобразования, что в результате приводило к открытию ее новых форм (так, например, "безвозвратная" потеря энергии в некоторых реакциях с участием элементарных частиц послужила указанием на существование еще одной неизвестной ранее элементарной частицы, впоследствии получившей название нейтрино).

Закон сохранения энергии имеет большое практическое значение, поскольку существенно ограничивает число возможных каналов эволюции системы без ее детального анализа. Так на основании этого закона оказывается возможным априорно отвергнуть любой весьма проект весьма экономически привлекательного вечного двигателя первого рода (устройства, способного совершать работу, превосходящую необходимые для его функционирования затраты энергии).

В основе закона сохранения энергии лежит однородность времени, т.е. равнозначность всех моментов времени, заключающаяся в том, что замена момента времени t₁ моментом времени t₂ без изменения значений координат и скоростей тел не изменяет механических свойств системы. Поведение системы, начиная с момента t₂, будет таким же, каким оно было бы, начиная с момента t₁.

Закон сохранения энергии имеет всеобщий характер. Он применим ко всем без исключения процессам, происходящим в природе. Полное количество энергии в изолированной системе тел и полей всегда остается постоянным; энергия лишь может переходить из одной формы в другую. Этот факт является проявлением неуничтожаемости материи и ее движения.

Причиной изменения скорости тела всегда является его взаимодействие с другими телами. При взаимодействии двух тел всегда изменяются скорости, т.е. приобретаются ускорения. Отношение ускорений двух тел одинаково при любых взаимодействиях. Свойство тела, от которого зависит его ускорение при взаимодействии с другими телами, называется инертностью. Количественной мерой инертности является масса тела. Отношение масс взаимодействующих тел равно обратному отношению модулей ускорений. Второй закон Ньютона устанавливает связь между кинематической характеристикой движения – ускорением, и динамическими характеристиками взаимодействия – силами. , или, в более точном виде, 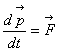, т.е. скорость изменения импульса материальной точки равна действующей на него силе. При одновременном действии на одно тело нескольких сил тело движется с ускорением, являющимся векторной суммой ускорений, которые возникли бы при воздействии каждой из этих сил в отдельности. Действующие на тело силы, приложенные к одной точке, складываются по правилу сложения векторов. Это положение называют принципом независимости действия сил. Центром масс называется такая точка твердого тела или системы твердых тел, которая движется так же, как и материальная точка массой, равной сумме масс всей системы в целом, на которую действуют та же результирующая сила, что и на тело. . Проинтегрировав это выражение по времени, можно получить выражения для координат центра масс. Центр тяжести – точка приложения равнодействующей всех сил тяжести, действующих на частицы этого тела при любом положении в пространстве. Если линейные размеры тела малы по сравнению с размером Земли, то центр масс совпадает с центром тяжести. Сумма моментов всех сил элементарных тяжести относительно любой оси, проходящей через центр тяжести, равна нулю.

Потенциальная энергия характеризует взаимодействующие тела, кинетическая – движущиеся. И та, и другая возникают в результате взаимодействия тел. Если несколько тел взаимодействую между собой только силами тяготения и силами упругости, и никакие внешние силы на них не действуют (или же их равнодействующая равна нулю), то при любых взаимодействиях тел работа сил упругости или сил тяготения равна изменению потенциальной энергии, взятой с противоположным знаком. В то же время, по теореме о кинетической энергии (изменение кинетической энергии тела равно работе внешних сил) работа тех же сил равна изменению кинетической энергии. . Из этого равенства следует, что сумма кинетической и потенциальной энергий тел, составляющих замкнутую систему и взаимодействующих между собой силами тяготения и упругости, остается постоянной. Сумма кинетической и потенциальной энергий тел называется полной механической энергией. Полная механическая энергия замкнутой системы тел, взаимодействующих между собой силами тяготения и упругости, остается неизменной. Работа сил тяготения и упругости равна, с одной стороны, увеличению кинетической энергии, а с другой – уменьшению потенциальной, то есть работа равна энергии, превратившейся из одного вида в другой.

Гидростатика. Равновесие жидкостей и газов.

Гидростатика – наиболее простой раздел гидроаэромеханики, который исследует ситуации, когда движение отсутствует или скорость пренебрежимо мала. Гидростатика позволяет понять некоторые свойства такой важной гидродинамической величины, как давление. Давление на опору оказывают и твёрдые, и сыпучие вещества, но оно отличается от гидростатического. Давление твёрдого тела определяется его весом, давление жидкости – её глубиной. Сила давления р на дно сосуда не зависит от его формы, а определяется только уровнем налитой в сосуд жидкости в соответствии с гидростатической формулой:

p = р_о + рgh

 

где р – плотность жидкости, g – ускорение свободного падения, h – глубина погружения, р_о – атмосферное давление.

Сыпучие тела, подобно жидкости и газу, могут оказывать давление на боковую поверхность, но для такого давления не выполняется закон Паскаля, утверждающий, что давление в любом месте покоящейся жидкости ил газа по всем направлениям одинаково, причём давление одинаково передаётся по всему объёму жидкости или газа. В законе Паскаля вес жидкости или газа не учитывается.

К основным законам гидростатики, помимо закона Паскаля и гидростатической формулы, можно отнести закон Архимеда: на погружённое в жидкость или газ тело действует выталкивающая сила, равная по величине весу вытесненной жидкости (или газа), направленная против силы тяготения и приложенная к центру тяжести вытесненного объёма.

Закон Архимеда и гидростатическую формулу можно вывести, используя стандартный для механики приём, иногда называемый правилом РОЗУ. РОЗУ это сокращёние до начальных букв алгоритма – РАЗРЕЖЕМ, ОТБРОСИМ, ЗАМЕНИМ, УРАВНОВЕСИМ. Например, с помощью алгоритма РОЗУ, закон Архимеда выводится так:

Если погружённое в жидкость тело заменить такой же жидкостью, то получиться состояние равновесия – на поверхность тела действует сила давления жидкости, которая уравновешивает вес жидкости внутри поверхности.

Движение жидкостей и газов.

Движение жидкостей и газов, как и все другие виды движения, рассматриваемые в механике, можно полностью охарактеризовать, оперируя единицами измерения длины, времени и силы. Так, диаметр парашюта можно измерять в метрах, время снижения, скажем, на 100 метров – в секундах, а вес груза – в ньютонах. Точно так же входное сечение насоса можно измерять в квадратных метрах, объемный расход среды – в кубических метрах в секунду, а мощность – в ньютон-метрах (джоулях) в секунду. Существует много способов измерения таких характеристик течения с использованием различных – механических и электрических – эквивалентов линейки, часов и пружинных весов. Например, скорость жидкостей и газов можно оценивать по числу оборотов в единицу времени проградуированной крыльчатки (гидрометрическая вертушка и анемометр) или по изменению электросопротивления нагреваемой проходящим током проволоки (проволочный термоанемометр); давление можно определять по вызываемому им отклонению изогнутой трубки или мембраны (манометр Бурдона и барометр-анероид) либо по току, генерируемому пьезокристаллом.

Прогнозирование характеристик течения.

Если бы такие измерения движения жидкостей и газов были единственным занятием гидроаэромеханики, это была бы дисциплина довольно узкого профиля. Гораздо более важное значение, чем измерение, имеет точное прогнозирование характеристик течения при заранее известных или предполагаемых условиях. Очевидно, что недостаточно уметь просто измерить пропускную способность построенного водослива, – нужно сначала надежно спроектировать водослив, рассчитанный на максимально возможный поток; точно так же измерить лагом скорость судна в плавании проще, чем заранее указать мощность двигателей, которые потребуются новому судну для поддержания заданной крейсерской скорости; напечатать в газете скорость ветра и атмосферное давление, измеренные вчера, гораздо легче, чем предсказать погодные условия на завтрашний день. Короче говоря, истинный предмет гидроаэромеханики – установление соотношений между различными характеристиками течения, позволяющих определить любую из них, коль скоро заданы другие характеристики, от которых она зависит.

Уравнение неразрывности.

Хотя гидроаэродинамика основана на трёх хорошо известных в механике законах сохранения массы, импульса и энергии, формулировки этих законов в ней выглядят сложнее. Например, обычное определение закона сохранения массы гласит, что масса системы тел остаётся неизменной. Для жидкости, текущей в трубе, этот закон используется в форме, называемой уравнением неразрывности. Уравнение неразрывности - соотношение между скоростью течения, объемным расходом среды и расстоянием между линиями тока. Это уравнение выражает один из основных законов гидроаэромеханики, согласно которому объемный расход во всякой трубке тока, ограниченной соседними линиями тока, должен быть в любой момент времени одинаков во всех ее поперечных сечениях. Поскольку объемный расход Q равен произведению скорости текущей среды V на площадь A поперечного сечения трубки тока, уравнение неразрывности имеет следующий вид:

Q = V₁A₁ = V₂A₂ или же vS = const ( v – скорость жидкости, S – площадь сечения трубы, по которой течёт жидкость. Смысл – сколько воды вливается – столько и должно вылиться, если условия течения неизменны).

Поэтому там, где сечение велико и линии тока разрежены, скорость должна быть мала, и наоборот. (Все три части этого двойного равенства должны выражаться в одной и той же системе единиц. Так, если величина Q выражена в м³/с, то скорость V должна выражаться в м/с, а площадь A – в м².)

Уравнение Бернулли.

Одно из важнейших уравнений гидромеханики было получено в 1738 году швейцарским учёным Даниилом Бернулли. Ему впервые удалось описать движение несжимаемой идеальной жидкости (силы трения между элементами идеальной жидкости, а также между идеальной жидкостью и стенками сосуда отсутствуют). Уравнение Бернулли имеет вид:

р + рv² + pgh = const.

2

 

где р – давление жидкости, р – её плотность, V – скорость движения, g – ускорение свободного падения, h – высота, на которой находится элемент жидкости.

Согласно уравнению Бернулли, в случае установившегося течения, для которого не имеют существенного значения все другие характеристики текущей среды, кроме плотности (удельного веса), полный напор одинаков во всех поперечных сечениях трубки тока. Если к отверстию в стенке трубы присоединить манометрическую трубку, то жидкость в такой трубке поднимется на высоту, равную гидростатическому напору. Если манометрическую трубку выставить навстречу потоку, то жидкость в манометре поднимется на дополнительную высоту, равную скоростному напору. Трубка, имеющая одновременно торцевое и боковые манометрические отверстия, называется трубкой Пито и используется для определения скорости течения по измеренному скоростному напору. Трубки Пито входят в комплект измерительного оборудования всех самолетов, а также широко применяются для измерений скорости течения в трубопроводах, вентиляционных воздуховодах, в аэро- и гидродинамических трубах.

Если скорость течения равна нулю (т.е. среда не движется), то уравнение Бернулли сводится к простому уравнению гидростатики.

Согласно этому уравнению, увеличению высоты в неподвижной среде жидкости или газа соответствует равное уменьшение гидростатического напора. Поэтому давление в любой точке неподвижной жидкости равно глубине этой точки под свободной поверхностью, умноженной на удельный вес жидкости. На основе этого соотношения вычисляется давление жидкости на стенки резервуаров, а также проводится анализ плавучести и остойчивости морских и речных судов.

В тех случаях, когда скорость течения отлична от нуля, уравнение Бернулли совместно с уравнениями неразрывности и закона сохранения количества движения позволяет решать практически важные задачи – о расходе среды, текущей через измерительные диафрагмы, поверх измерительных и водосбросных водосливов и под затворы шлюзовых галерей; о траектории струи жидкости; о форме, скорости и силе волн, действующих на суда и волноломы. Хотя в таких задачах обычно рассматривается течение воды под атмосферным слоем воздуха, аналогичные процессы гравитационного характера имеют место в случае течения более холодной (и, следовательно, более плотной) воды под более теплой, как и других жидкостей и газов разной плотности. Таким образом, водным потокам в реках аналогичны океанские течения и ветры, поскольку все гравитационные явления подчиняются одним и тем же законам гидроаэромеханики.

Гравитационное моделирование. Число Фруда.

Хотя многие задачи такого рода решаются с приемлемой точностью, существует много других сложных задач, аналитическое решение которых пока невозможно. Тем не менее удовлетворительное решение ряда таких задач можно находить путем моделирования с использованием теории подобия. Влияние силы тяжести на картину потока характеризуется безразмерной величиной (критерием подобия), составленной из некой характерной скорости V, характерной длины L, разности Dg удельных весов верхней и нижней текущих сред и плотности r одной из них:

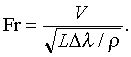
Эта величина называется числом Фруда. Очевидно, что в случае течения воды под атмосферным воздухом мы имеем просто . Подобие будет обеспечено только в том случае, если число Фруда для модели равно числу Фруда для реального объекта (т.е., например, скорость модели судна должна быть уменьшена пропорционально квадратному корню из уменьшения размера). Такого рода экспериментальные исследования уменьшенных моделей – обычная практика при проектировании судов и речных гидротехнических сооружений; более того, в настоящее время методы моделирования распространяются на аналогичные гравитационные задачи метеорологии и океанографии.

Гидродинамика Эйлера и Навье-Стокса.

Выводя дифференциальное уравнение движения идеальной жидкости, Леонард Эйлер полагал, что силы, действующие на любую поверхность в ней, так же как и в неподвижной жидкости, перпендикулярны самой этой поверхности. Такое предположение позволило описать движение жидкости аналитически. Однако иногда теория идеальной жидкости Эйлера перестаёт работать.

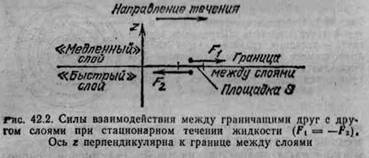
Реальная жидкость отличается от идеальной тем, что она обладает внутренним трением, или вязкостью. Два соприкасающихся элемента жидкости, двигающиеся в одном и том же направлении, но с разными скоростями, воздействуют друг на друга. Сила взаимодействия ускоряет медленно движущийся элемент жидкости и замедляет более быстрый. Ньютон предположил, что величина этой силы (сила внутреннего трения) пропорциональна разности скоростей элементов жидкости. Закон вязкого трения Ньютона гласит, что сила внутреннего трения F пропорциональна изменению скорости жидкости v в направлении, перпендикулярном движению, и зависит от площади S соприкосновения элементов жидкости. Коэффициент пропорциональности в нём называется коэффициентом динамической вязкости ( n ).

F = n ^dv S

^dy

 

Жидкости, в которых внутреннее трение подобным образом зависит от изменения скорости, называются жидкостями с линейной вязкостью, или ньютоновскими жидкостями.

Величину коэффициента динамической вязкости Ньютон определил с помощью опыта: передвигая по поверхности жидкости плоскую пластину с разной скоростью, он заметил, что для поддержания определённой скорости требуется сила, которая при небольшой глубине жидкости оказалась прямо пропорциональна площади S и скорости пластины v и обратно пропорциональна глубине жидкости h.

F = n v S

h

Несмотря на то, что при увеличении глубины жидкости сила вязкого трения пластинки не становится исчезающе малой, эта формула довольно точно описывает взаимодействие между соприкасающимися элементами жидкости. Чем больше разность скоростей, тем больше сила, с которой они воздействуют друг на друга, заставляя притормаживать более быстрые элементы и разгоняя медленные. В результате относительное движение в жидкости прекращается.

В более строгой формулировке линейная зависимость вязкого трения от изменения скорости движения жидкости называется уравнением Навье-Стокса. Оно учитывает сжимаемость жидкостей и газов и справедливо не только вблизи поверхности твёрдого тела, но и в каждой точке жидкости. Любые газы, для которых выполняется условие сплошности, подчиняются уравнению Н-С, т. е. Являются ньютоновскими жидкостями.

Влияние вязкости на картину течения.

Вязкость жидкости и газа обычно существенна только при относительно малых скоростях, поэтому гидродинамика Эйлера – это частный предельный случай больших скоростей гидродинамики Стокса. При малых скоростях в соответствии с законом вязкого трения Ньютона сила сопротивления тела пропорциональна скорости. При больших скоростях, когда вязкость перестаёт играть существенную роль, сопротивление тела пропорционально квадрату скорости.

Этот критерий называется числом Рейнольдса и имеет вид.

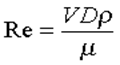
число Рейнольдса – безразмерная величина, которая характеризует относительную роль сил вязкости.

Оно играет такую же роль в моделировании влияния вязкости, что и число Фруда при моделировании гравитационных эффектов, а потому служит основой опытов, проводимых в аэродинамических трубах с моделями самолетов, и градуировок расходомеров для жидкостей разной вязкости – в общем, при исследовании всех видов течений по трубам и с обтеканием тел во всех случаях, когда доминирует влияние вязкости. Если равенство чисел Фруда для модели и натурного объекта требовало уменьшения скорости модели в связи с ее уменьшенными размерами, то равенство чисел Рейнольдса, наоборот, требует, чтобы скорость модели увеличивалась с уменьшением ее размеров. Поэтому, чтобы не нужно было чрезмерно повышать скорость в экспериментах с уменьшенными моделями, часто применяют текучие среды с меньшей вязкостью или большей плотностью; так, в аэродинамических трубах нередко повышают давление до нескольких атмосфер, что позволяет снизить скорость за счет повышения плотности.

Турбулентное течение в трубах.

Течение вязкой жидкости вдоль границы может оказаться неустойчивым по отношению к малым возмущениям, если число Рейнольдса превысит некоторое значение. Так, например, течение в трубе постоянного диаметра устойчиво ко всем возмущениям, если число Рейнольдса VDr/m меньше приблизительно 2000, и тогда формула Пуазейля дает соотношение между перепадом давления и скоростью независимо от плотности. Но когда число Рейнольдса превышает указанное критическое значение, любое локальное возмущение вызывает колебания скорости или образование завихрений, которые быстро распространяются по всему потоку, создавая беспорядочное вторичное движение, называемое турбулентным течением. Из-за бесчисленных вихрей турбулентное течение характеризуется значительно большей затратой энергии (более высокими потерями давления), чем устойчивое, или ламинарное, течение, и формула Пуазейля в этом случае заменяется формулой

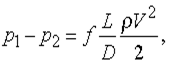
где коэффициент f зависит от числа Рейнольдса и относительной шероховатости поверхности трубы. В случае гладкой трубы, например, f = 0,316/Re^1/4, тогда как при аналогичных условиях формула Пуазейля дает f = 64/Re. Чем больше шероховатость поверхности, тем, очевидно, больше величина f ; если шероховатость трубы достаточно велика, то при больших числах Рейнольдса коэффициент f перестает зависеть от вязкого сдвига и полностью определяется неровностями стенок, вызывающих завихрения.

Гидравлический удар.

С точки зрения гидроаэромеханики жидкости и газы очень схожи между собой. Однако, плотность жидкости во много раз больше плотности газа. Поэтому гребные винты морских и речных судов сравнительно меньше пропеллеров самолётов – тяжёлая жидкость «работает» эффективнее, чем лёгкий воздух. По той же причине жидкость может оказаться опаснее и привести к аварии.

При внезапном перекрывании воды, давление в трубе возрастает на величину pva, где р – плотность жидкости или газа, v – скорость течения и а – скорость звука. Скорость звука в трубе с водой равна 1400 м/с, поэтому именно с такой скоростью будет распространяться повышенное давление по трубопроводу. Если где-то обнаружиться непрочный участок трубы, он будет прорван. Газ, в сравнении с жидкостью, имеет гораздо меньшую плотность, да и скорость звука в нём в несколько раз меньше, поэтому газ, даже находящийся под большим давлением, не может создать удар, подобный гидравлическому.

Гидравлический удар может быть направлен и в обратную (от заслонки) сторону. Это произойдёт, если резко перекрыть воду, поток которой достаточно протяжённый. Жидкость, двигаясь по инерции, оторвётся от заслонки, а пространство между заслонкой и жидкостью заполниться водяным паром под очень низким давлением (сродни вакууму). В конечном итоге, поток жидкости под действием внешнего давления затормозится, остановится и с нарастающей скоростью двинется в противоположном направлении.

Гидравлический удар может также сыграть полезную роль. Если повреждение уже имеется, отыскать его расположение поможет небольшой гидравлический удар. Он создаст волну, бегущую по трубопроводу, которая, отразившись от места повреждения, вернётся через некоторое время. По этому времени легко определить расстояние до повреждённого участка.

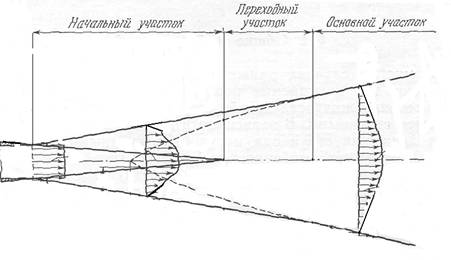
Явления в пограничном слое.

В случае течения указанного вида по длинной трубе влияние стенок на характер течения распространяется и на центральную часть трубы. В случае же обтекания тела средой замедляющее действие вязкого сдвига вдоль поверхности тела (на которой скорость равна нулю) обычно распространяется в окружающую среду лишь на сравнительно небольшое расстояние. Относительная толщина этого т.н. пограничного слоя зависит от числа Рейнольдса, составленного из относительной скорости, плотности и вязкости текучей среды и расстояния от рассматриваемой точки до передней кромки тела. При малых значениях Re пограничный слой будет ламинарным, но течение становится неустойчивым по отношению к малым возмущениям, когда Re приближается к 4×10⁶, а после этого развивается турбулентность. Вязкий сдвиг вдоль граничной поверхности теперь аналогичен перепаду давления вдоль трубы и точно так же зависит от числа Рейнольдса. Полная сила сопротивления течению F_D, создаваемая участком поверхности длиной L и шириной B, дается выражением

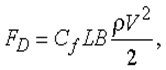
где C_f – коэффициент сопротивления, зависящий от Re = VLr/m и от шероховатости поверхности. Для гладкой поверхности C_f = 1,33/Re^1/2, если пограничный слой ламинарный, и C_f = 0,074/Re^1/5, если пограничный слой полностью турбулентный. Это соотношение играет очень важную роль в расчетах сопротивления крыла и фюзеляжа самолета, а также корпуса речного или морского судна. Теория пограничного слоя разработана Л.Прандтлем (1875–1953).

Наряду с поверхностным сопротивлением, возникающим в пограничном слое, в этом слое наблюдается еще одно важное явление – отрыв течения от стенки при резком изменении ее геометрии. Вязкая текучая среда при больших числах Рейнольдса не следует точно за изломом стенки и не смыкается без возмущений даже позади хорошо закругленного тела, например сферического. Для предотвращения отрыва потока задней части тела придают обтекаемую форму и точно так же сглаживают (профилируют) трубу переменного диаметра (сопло Лаваля). Явление отрыва связано с высокими градиентами давления и скорости течения в пограничном слое, и такая тенденция заметно ослабевает, если отводить текучую среду из пограничного слоя. Поэтому, в частности, предусматривают прорези на крыльях и фюзеляже самолета для слива пограничного слоя.

Отрыв потока, вообще говоря, нежелателен, поскольку он обычно возникает в точках максимальной скорости и, следовательно, минимального давления, после чего это низкое давление доминирует во всей зоне отрыва ниже по течению. В результате течение воздействует на поверхность тела (стенку) с некоторой силой, добавляющейся к поверхностному сопротивлению (создавая «сопротивление формы», обусловленное повышенным давлением спереди обтекаемого тела и пониженным – сзади), а энергия течения «непроизводительно» расходуется на интенсивную турбулентность, возникающую в неустойчивой зоне отрыва. Для погруженных в поток тел сочетание поверхностного сопротивления и сопротивления формы дает полную силу сопротивления движению, зависящую, таким образом, от формы тела и от числа Рейнольдса, а именно, если обозначить площадь поперечного сечения тела через A:

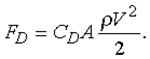
Для сферы при малых числах Рейнольдса (менее 1) формула Стокса принимает вид C_D = 24/Re; при Re £ 10⁵ пограничный слой является ламинарным и C_D = 0,5; при Re £ 10⁶ пограничный слой становится турбулентным и C_D = 0,2. Для парашюта сопротивление должно быть максимальным и C_D = 1,3, тогда как для высокоскоростного самолета коэффициент C_D может составлять лишь 0,05.

Вихревые колебания.

В случае удлиненных тел, скажем цилиндрических, закономерности сопротивления среды оказываются примерно такими же, как и для сфер, но, кроме того, происходят поперечные колебания зоны отрыва течения. Поскольку при этом зона пониженного давления оказывается то с одной, то с другой стороны от направления движения (вихревая дорожка фон Кармана), на тело действует не только продольная сила лобового сопротивления, но и переменная поперечная сила. Этим объясняются вибрация перископов высокоскоростных подлодок и гудение проводов при сильном ветре. Частота такой вибрации тоже зависит от числа Рейнольдса; например, для цилиндра при Re = 10⁵ и ламинарном пограничном слое период колебаний t определяется равенством Vt/D = 5; когда же пограничный слой становится турбулентным, этот численный множитель уменьшается в два раза.

Плоская поверхность.

 Сходную поперечную силу отрыв потока вызывает в случае плоской поверхности, наклоненной, подобно воздушному змею, относительно направления течения, но в этом случае боковая сила не меняет периодически своего направления. На тонкую пластину, находящуюся в потоке под углом атаки к нему, также действует заметная сила сопротивления, обусловленная понижением давления в зоне отрыва, но эту силу можно существенно уменьшить (при одновременном увеличении поперечной силы), если придать пластине утолщенный профиль, закругленный спереди и слегка искривленный («вогнуто-выпуклый»). Такое тело, называемое аэродинамической поверхностью или попросту крылом, создает подъемную силу, за счет которой летают самолеты (теория крыла разработана русскими учеными Н.Е.Жуковским (1847–1921) и С.А.Чаплыгиным (1869–1942)), а в виде подводного крыла используется на скоростных речных и морских судах. Искусство проектирования таких профилей достигло столь высокого уровня, что легко обеспечиваются подъемные силы, в 30 и более раз превышающие лобовое сопротивление

Сила, действующая на крыло (или руль) в потоке, дается выражением:

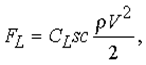
где s – размах (длина), а c – хорда (ширина) крыла. При больших числах Рейнольдса величина C_L зависит практически только от формы и угла наклона профиля; приемлемой величиной для крыла можно считать C_L = 0,5 .

Поверхности другой формы.

Поверхности, создающие подъемную силу, используются в конструкциях крыла самолетов и других скоростных судов; на основе тех же принципов проектируются лопасти воздушных и гребных винтов, лопатки и лопасти рабочих колес турбин, насосов, компрессоров, гидродинамических передач. В испытаниях устройств и машин такого рода определяют коэффициенты тяги, всасывания, мощности (гребного винта), напора и подачи, аналогичные коэффициентам подъемной силы и лобового сопротивления для аэродинамической поверхности. Всякий такой коэффициент зависит от формы поверхности и от числа Рейнольдса, при котором она должна работать, и оценка этих коэффициентов по данным модельных экспериментов производится на основе тех же самых законов подобия. Важное значение имеет то обстоятельство, что рабочие характеристики любой модели можно, исходя из соображений удобства, изучать как в воде, так и в воздухе независимо от назначения проектируемого устройства при условии, что воспроизводится число Рейнольдса и другие определяющие критерии.

Сжимаемость.

Хотя сжимаемость (или ее обратная величина – упругость) является свойством, которое, строго говоря, выводит нас за рамки гидроаэромеханики, ее, по крайней мере при упрощенной постановке задачи, приходится учитывать по соображениям двоякого рода. Во-первых, реальные жидкости и газы представляют собой упругие среды, и звуковые волны распространяются в них со скоростью, которая вычисляется по одной и той же формуле. Если скорость звука обозначить через с, а модуль упругости – через E, то формула запишется в виде

(Скорость звука с в воздухе составляет 335, а в воде – около 1430 м/с.) Если течение в трубопроводе резко перекрыть краном или задвижкой, то возмущение от остановки течения будет распространяться вверх по трубопроводу со скоростью звука, причем уменьшение скорости среды позади такой волны возмущения будет сопровождаться заметным повышением давления. В случае жидкости повышение давления при внезапном перекрытии трубопровода может быть очень большим, и пики давления при взаимодействии прямой и обратной волн представляют собой опасный эффект, называемый гидравлическим ударом. Явление распространения звука в воде, как и в воздухе, имеет и свои полезные стороны – на этом основаны гидролокация и аппаратура для обнаружения подлодок.

Во-вторых, сжимаемость приходится учитывать и по той причине, что именно этим свойством определяется возможность анализа жидкости и газа на основе одних и тех же принципов. Критерием при этом служит отношение скорости течения к скорости упругой волны, т.е. к скорости звука в данной среде:

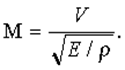
Этот критерий называется числом Маха. (Отметим, что число Маха аналогично числу Фруда, так как последнее есть отношение скорости течения к скорости гравитационной волны.) До тех пор пока величина М мала (£ 0,5), влияние сжимаемости незначительно. Когда же число Маха приближается к единице, картина течения существенно изменяется в связи со звуковыми эффектами. Например, коэффициент лобового сопротивления снаряда со сферической головной частью зависит только от числа Рейнольдса, пока число Маха не превысит 0,5; после этого он постепенно возрастает и приблизительно удваивается, когда число Маха становится больше единицы, вследствие образования звуковых волн (скачков уплотнения) в зоне сжатия непосредственно перед снарядом. Подобно тому как носовой части быстроходных судов придают заостренную и тщательно спрофилированную форму для уменьшения носовой волны и, следовательно, волнового сопротивления, заостряют высокоскоростные снаряды и носовые части и передние кромки крыльев самолетов, чтобы уменьшить потери в скачках уплотнения, а тем самым уменьшить сопротивление, связанное со звуковыми эффектами. О больших энергетических потерях, обусловленных образованием звуковых волн, можно судить по тому шуму, который создают воздушные винты самолетов, и по пронзительному звуку, которым сопровождается полет снарядов и ракет.

 

 

Аналогии между течением жидкости и газа.

 Тесная аналогия между процессами образования волн «маховского» и «фрудовского» типов дает возможность исследователям, работающим в обоих этих направлениях, собирать ценные плоды, выращенные на общей почве гидроаэромеханики. Так, анализ картины звуковых волн, примененный к картине гравитационных волн в сбросных противопаводковых каналах, позволил существенно усовершенствовать планировку таких каналов. И наоборот, исследования высокоскоростных моделей в сверхзвуковых аэродинамических трубах обычно дополняются исследованиями в буксировочных опытных бассейнах и гидродинамических лотках, где картину волн, создаваемых такими телами, можно изучать визуально. Наряду с такой аналогией между течением жидкостей и газов имеется и различие, которое, однако, тоже служит полезной цели как основа для сравнения. Когда скорость газа в какой-либо точке достигает скорости звука, в этой точке, как уже говорилось, может возникнуть звуковая волна. Скорость жидкости из-за практических ограничений вряд ли когда-либо сможет приблизиться к скорости звука, но в жидкости существует предел, налагаемый давлением насыщенного пара самой жидкости, для понижения давления, связанного с увеличением скорости. Когда скорость жидкости сильно возрастает в какой-либо ее точке, вследствие соответствующего снижения давления жидкость в этой точке вскипает. Это явление называется кавитацией. Быстрое образование тотчас же при повышении давления схлопывающихся пузырьков пара приводит не только к снижению коэффициента полезного действия насосов и гребных винтов, но и к их механическому повреждению и разрушению, если такой процесс продолжается достаточно долго. Аналогия же с течением газа кроется здесь в том, что зоны, опасные для обтекаемого тела, одинаковы как при образовании звуковых волн в воздухе, так и при возникновении кавитации в воде. Но кавитацию легко наблюдать по помутнению прозрачной воды (появлению в ней пузырьков), тогда как для наблюдения звуковых волн необходимо специальное оптическое оборудование. Поэтому модели, для которых существенны звуковые эффекты в воздухе, часто испытывают на кавитацию в гидродинамических трубах, что позволяет усовершенствовать конструкцию и устранить многие опасные зоны.

Заключение.

На мой взгляд, не стоит в очередной раз перечислять те законы, явления и приводить уже освещённые мной формулы. Подводя итог изложенному, остановлюсь на суммировании тех понятий, которые были описаны ранее и постараюсь логически обосновать их значимость для науки и в повседневной жизни.

Как известно, наука имеет свои характерные отличительные черты. Она:

1.  универсальна

2.  фрагментарна

3.  общезначима

4.  обезличена

5.  систематична

6.  незавершённа

7.  преемственна

8.  критична

9.  достоверна

10.  внеморальна

11.  рациональна

12.  чувственна

Кроме того, для науки характерны свои особые методы и структура исследований, а так же язык и аппаратура. Всем этим определяются специфика научного исследования и значение науки.

Отправной точкой для каждого научного исследования и дальнейшего открытия служит обычный эмпирический факт. В случае с гидроаэромеханикой это может быть факт полёта птиц или пересекающий океан кокосовый орех.

Далее, следует определённый метод исследования именуемый наблюдением. Зачастую, процесс наблюдения требует привлечения аппаратуры и других вспомогательных средств. В отношении точных наук, таких как механика, помимо голых фактов необходимо всё предшествующее знание, касающееся данной проблемы, прежде всего – знание принципов механики (трёх законов Ньютона). Роль наблюдения заключается в том, чтобы подтвердить эмпирический факт путём проверки справедливости этого явления относительно других аналогичных объектов (остальных птиц, например).

Убедившись в том, что некоторые предметы могут плыть, а птицы летать, неминуемо задаёшься вопросами «как?» и «почему?». Это ведёт к выдвижению определённой гипотезы, для подтверждения (или опровержения) которой можно провести эксперимент. Существует множество разновидностей эксперимента: от мысленного (когда объекты вымышлены, а сам экспериментальный процесс проводиться в уме), до модельного (когда эксперимент проводится с помощью моделей, размеры и масса которых пропорционально уменьшены по сравнению с реальными телами). В зависимости от исследуемого объекта, возможен эксперимент с идеализациями, т.е. идеальными представлениями (идеальная жидкость). Чтобы из наблюдения различных явлений сделать общие выводы, надо установить количественные зависимости между различными величинами – физические законы. Установленные физические законы избавляют от необходимости проводить опыт в каждом конкретном случае. Отличительной особенностью научного эксперимента является то, что его должен быть способен воспроизвести каждый исследователь в любое время. Если гипотеза подтверждается экспериментами и проходит испытание принципом фальсифицируемости – можно судить о её достоверности и перевести данную гипотезу в разряд теорий.

Механика жидкости и газа является особым разделом физики. Как уже говорилось ранее, в основу её входят несколько основных законов. Эти законы актуальны не только по отношению к рассмотренным фазам вещества, но и для твёрдых тел (правда, с небольшими «подгонками» под физическую суть этих тел). Для наибольшего удобства и краткости, законы отражены в математических формулах – языке науки. На основе этих законов созданы различные механизмы, которыми окружил себя человек. Механизмы сильно облегчают и ускоряют процессы производства, да и физический труд человека как таковой. Лишь благодаря достижениям в области точных наук стало возможным освоить то, что было недосягаемо для человека ранее. Это глубины океана, возможность передвижения в атмосфере, полёты в космос и многое другое. И наука не стоит на месте. С каждым днём учёные приближают нас на шаг ближе к познанию жизни. Полностью познать Вселенную, конечно, невозможно, но осмыслить то, что доступно человеку со временем неминуемо.

Список использованной литературы.

1.  Энциклопедия «Аванта+», Т. 16 (I, II части) - М.: Аванта+, 2001г.

2.  Г. Я. Мякишев, Б. Б. Буховцев «Физика» - М.: Просвещение, 1997г.

3.  И. К. Кикоин, А. К. Кикоин «Физика» - М.: Просвещение, 1992г.

4.  О. К. Костко «Механика». –М.: Лист, 1998г.

5.  Н. А. Эрдеди, А. А. Эрдеди «Теоретическая механика, сопротивление материалов». –М.: Высшая школа,2002г.

6.  Интернет ресурсы.