Навигация
ТЕОРИЯ РАСЧЕТА ЭЛЕКТРИЧЕСКИХ ПОЛЕЙ
2. ТЕОРИЯ РАСЧЕТА ЭЛЕКТРИЧЕСКИХ ПОЛЕЙ
Алгоритм расчета разработан с учетом [11, 12, 13, 14, 15].
Напряженность в точке М пространства![]() , кВ/м от заряда i - го проводника
, кВ/м от заряда i - го проводника ![]() , Кл равна:
, Кл равна:

где ![]() – расстояние, м от точки М в пространстве до i - ого заряда
– расстояние, м от точки М в пространстве до i - ого заряда ![]() ;
;
![]() –диэлектрическая проницаемость вакуума,
–диэлектрическая проницаемость вакуума, ![]() Ф/м.
Ф/м.
Чтобы получить формулы для расчета мгновенных, максимальных и действующих значений напряженности электрического поля в пространстве, окружающем линию электропередачи, сначала совмещаем комплексную плоскость с плоскостью поперечного сечения линии.
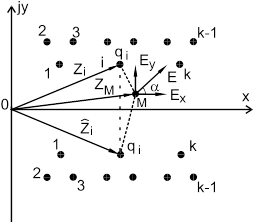
Рисунок 2.1 - Расположение проводников линии электропередачи в комплексной плоскости |
Затем для данной точки М плоскости записываем уравнения для горизонтальной ![]() и вертикальной
и вертикальной ![]() составляющих, создаваемых линейными зарядами ( k ) проводников линии
составляющих, создаваемых линейными зарядами ( k ) проводников линии

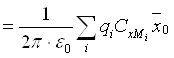 ; (2.1)
; (2.1)

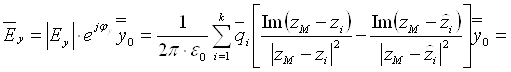
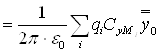 ,
,

где ![]() – единичный вектор в направлении оси х;
– единичный вектор в направлении оси х;
![]() – единичный вектор в направлении оси y;
– единичный вектор в направлении оси y;
![]() – координата точки М, в которой вычисляется напряженность;
– координата точки М, в которой вычисляется напряженность;
![]() – координаты i - ого проводника линии электропередачи;
– координаты i - ого проводника линии электропередачи;
![]() – координаты зеркально отраженного заряда i - ого проводника линии;
– координаты зеркально отраженного заряда i - ого проводника линии;
![]() - комплексные заряды на i - ых проводниках ЛЭП, которые вычисляется по уравнениям Максвелла в матричной форме:
- комплексные заряды на i - ых проводниках ЛЭП, которые вычисляется по уравнениям Максвелла в матричной форме:
![]() , откуда
, откуда 
где ![]() – столбцовая матрица комплексных напряжений, В;
– столбцовая матрица комплексных напряжений, В;
![]() – столбцовая матрица потенциальных коэффициентов;
– столбцовая матрица потенциальных коэффициентов;
![]() – столбцовая матрица комплексных зарядов, проводников, Кл.
– столбцовая матрица комплексных зарядов, проводников, Кл.
переходя к мгновенным значениям
![]() , (2.2)
, (2.2)
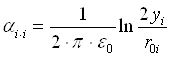 ;
;
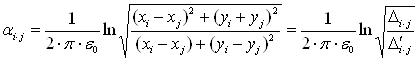
где ![]() – потенциальные коэффициенты;
– потенциальные коэффициенты;
![]() – радиус i - го проводника, м;
– радиус i - го проводника, м;
![]() и
и ![]() – соответственно амплитудное значение и фаза заряда на i - ом проводнике;
– соответственно амплитудное значение и фаза заряда на i - ом проводнике;
![]() и
и ![]() – соответственно амплитуда и фаза напряжения на i - ом проводнике.
– соответственно амплитуда и фаза напряжения на i - ом проводнике.
Амплитудное значение фазного напряжения на проводниках линии определяется через действующее значение номинального линейного напряжения как ![]()
На основании (2.1) и (2.2) можно заключить, что мгновенные значения вертикальной и горизонтальной составляющих напряженности в данной точке пространства изменяются во времени по закону синуса:
![]() ; (2.3)
; (2.3)
![]() ;
;
Мгновенное значение результирующей напряженности согласно рисунку 2.1:
![]() (2.4)
(2.4)
где ![]() и
и ![]() – соответственно амплитуды и мгновенные значения горизонтальной и вертикальной составляющих напряженности поля;
– соответственно амплитуды и мгновенные значения горизонтальной и вертикальной составляющих напряженности поля;
![]() и
и ![]() – фазы горизонтальной и вертикальной составляющих напряженности поля, которые, как следует из (2.1) равны;
– фазы горизонтальной и вертикальной составляющих напряженности поля, которые, как следует из (2.1) равны;
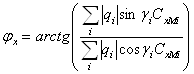
 (2.5)
(2.5)
Записывая результирующую напряженность как вектор, изменяющийся во времени и на комплексной плоскости (пространстве), получим
![]() (2.6)
(2.6)
где с учетом (2.3)
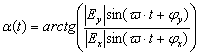 (2.7)
(2.7)
![]() (2.8)
(2.8)
где ![]() – направление результирующего вектора
– направление результирующего вектора ![]() в данный момент времени;
в данный момент времени;
![]() – мгновенное значение этого вектора.
– мгновенное значение этого вектора.
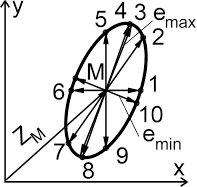
Анализ выражений (2.7) и (2.8) показывает, что в каждой точке пространства, окружающего проводники линии электропередачи, конец результирующего вектора напряженности электрического поля ![]() , описывает эллипс (рисок 2.2 б) за период времени, равный периоду изменения напряжения на фазах линии электропередачи.
, описывает эллипс (рисок 2.2 б) за период времени, равный периоду изменения напряжения на фазах линии электропередачи.
| а | б |
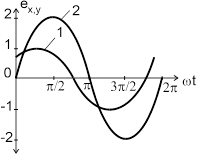
Рисунок 2.2 - Изменение электрического поля в точке М плоскости поперечного сечения линии: а - во времени горизонтальной Ex и вертикальной Ey составляющих; б - в пространстве направления a и во времени Т результирующей напряженности Е
| 1) a = 0°, T=0; 2) a = 54,7°, T = 45; 3) Emax, a = 68,34°, T=82,98; 4) a = 70,5°, T=90; 5) a = 90°, T=135; 6) a = 180°, T=180; 7) a = 234°, T=225; 8) a = 250,5°, T=270; 9) a = 270°, T=315; 10) Emin, a = - 21,66°, T= -7,02; |
Таким образом, в какие - то моменты времени величина результирующего вектора ![]() принимает максимальное и минимальное значения. Чтобы найти эти экстремальные значения, нужно взять производную по времени от выражения и приравнять ее к нулю:
принимает максимальное и минимальное значения. Чтобы найти эти экстремальные значения, нужно взять производную по времени от выражения и приравнять ее к нулю:
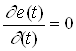 (2.9)
(2.9)
Решая уравнение (2.9), с учетом (2.8) получаем значения времени, при которых ![]() принимает экстремальные значения:
принимает экстремальные значения:

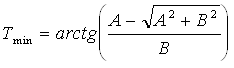 (2.10)
(2.10)
где
![]() ;
;
![]()
Подставляя (2.10) в (2.7) и (2.8), находим экстремальные значения результирующей напряженности поля:
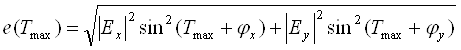 (2.11)
(2.11)
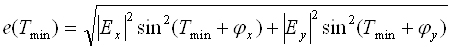
а так же их направления:
 (2.12)
(2.12)
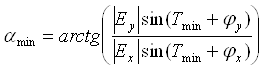
Действующее значение напряженности в точке М пространства найдем по формуле изменения периодической величины:
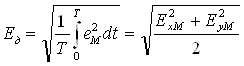 (2.13)
(2.13)
Таким образом, горизонтальная ![]() и вертикальная
и вертикальная ![]() составляющие внешнего поля, создаваемого проводниками линии, синусоидальны, тогда как закон изменения во времени результирующего поля
составляющие внешнего поля, создаваемого проводниками линии, синусоидальны, тогда как закон изменения во времени результирующего поля ![]() не синусоидален.
не синусоидален.
На рисунке 2.2 в качестве примера, представлены графики, показывающие изменение величин ![]() во времени и пространстве, для случая
во времени и пространстве, для случая ![]()
0 комментариев