Технические характеристики реле РС52

2. Технические характеристики реле РС52

Реле РС52 – открытое, одностабильное, с двумя контактными группами, с сочетанием размыкающих, замыкающих и переключающих контактов, предназначено для коммутации электрических цепей постоянного и переменного тока частотой до 400 Гц.

Реле РС52 соответствует требованиям ГОСТ 16121-86 и техническим условиям КЩО-450-017ТУ.

Условия эксплуатации

Температура окружающей среды от – 60 до + 70 °C.

Циклическое воздействие температур -60 и +70 °C.

Повышенная относительная влажность до 98 % при температуре +20 °C.

Атмосферное давление от 2´10³ до 106´10³ Па.

Синусоидальная вибрация (вибропрочность и виброустойчивость) в диапазоне частот от 5 до 80 Гц – с ускорением не более 100 м/с².

Ударная прочность

При многократных ударах с ускорением не более 1500 м/с² – 250 ударов, с ускорением не более 750 м/с² – 4000 ударов.

Постоянно действующие линейные ускорения не более 200 м/с².

Технические характеристики

Ток питания – постоянный.

Сопротивление изоляции между токоведущими элементами, между токоведущими элементами и корпусом, МОм, не менее:

- в нормальных климатических условиях (обмотки обесточены) 200

- в условиях повышенной влажности 10

- при максимальной температуре (после выдержки обмотки под рабочим напряжением) 200

Испытательное переменное напряжение, В:

между токоведущими элементами, между токоведущими элементами и корпусом:

- в нормальных климатических условиях 900

- в условиях повышенной влажности 500

- при пониженном атмосферном давлении 250

между изолированными обмотками:

- в нормальных климатических условиях 500

- в условиях повышенной влажности 300

- при пониженном атмосферном давлении 250

Сопротивление электрического контакта в стадии поставки 0,5 Ом, в процессе эксплуатации и хранения 2 Ом. Масса реле не более 110 г.

3. Расчет электромагнитного реле

 

Расчет проводимости рабочего зазора

Расчет магнитной цепи сводится к вычислению магнитной проводимости рабочего и нерабочего воздушных зазоров, проводимости утечки, коэффициента рассеяния потока и производной проводимости рабочего зазора для нескольких положений якоря.

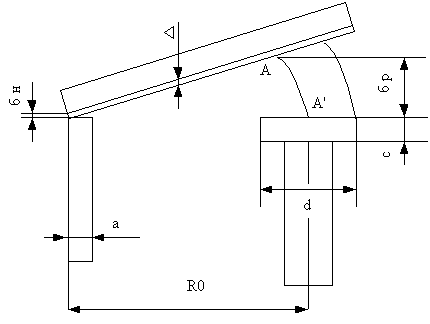Рисунок 1 - эскиз воздушных зазоров

Исходные данные:

Ширина полюсного наконечника d=0,017м;

Толщина полюсного наконечника c=0,00005 м.

Расстояние от оси вращения якоря до оси симметрии сердечника магнитной системы R₀=0,01425 м.

 5.толщина немагнитной прокладки =0.001м;

6.толщина скобы a=0,003 м;

Расчетная формула для проводимости имеет вид:

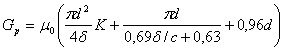,(3.1.1)

где:d - величина рабочего воздушного зазора;

h₀ =4p×10^{-7 Гн}/_м - магнитная постоянная;

К – коэффициент, учитывающий неравномерность магнитного поля

, r=2R₀/d=1,68

где R_р – магнитное сопротивление рабочего воздушного зазора, Гн^-1.

Затем рассчитаем магнитное сопротивление рабочего воздушного зазора R_р по формуле:

; (3.1.2)

Производная магнитной проводимости имеет вид:

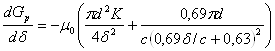.(3.1.3)

Вычисления магнитной проводимости производятся для трех значений рабочих воздушных зазоров: d₁=0,5×10^-3 м; d₂=1×10^-3 м; d₃=1,5×10^-3 м.

Полученные значения магнитной проводимости и производной магнитной проводимости сводим в табл. 1.

при δ_р1= 0,5 ·10^-3м:

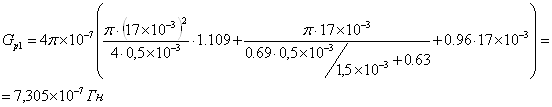
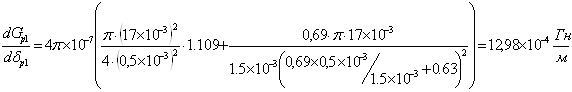
при δ_р2=1,0 ·10^-3м:

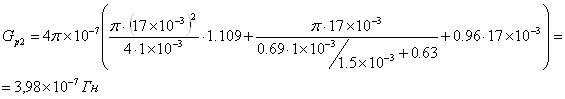
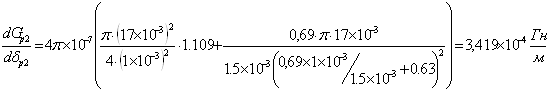
при δ_р3=1,5 ·10^-3м:

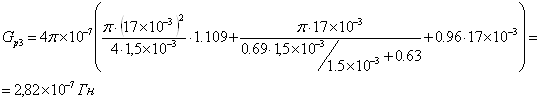
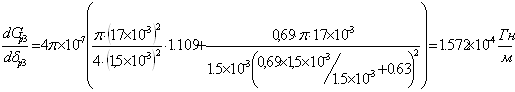
Таблица 1 – Значения магнитной проводимости и производной магнитной проводимости.

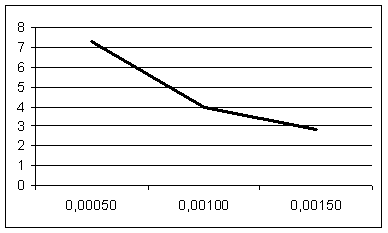
dp×10-3, м	0,5	1,0	1.5
Gp×10-7, Гн	7,305	3,98	2,82
Rp×10-7, Гн-1	0.1369	0.2513	0.355
×10-4, Гн/м	12.98	3.419	1.572

Построим график зависимости G_p=f(d_p) Рисунок 2

Расчет магнитной проводимости нерабочего зазора

Рассчитаем магнитную проводимость нерабочего воздушного зазора, который находится между прямоугольным якорем, расположенным под углом, и прямоугольной скобой. При этом принимаем следующие допущения:

зазор образован двумя параллельными плоскостями;

краевые потоки равны нулю и магнитная проводимость определяется по упрощенной формуле:

,(3.2.1)

гдеG_н- магнитная проводимость нерабочего зазора, Гн;

S_н- площадь нерабочего зазора, м²;

δ_н- величина нерабочего зазора, м;

значение нерабочего зазора определяется посередине скобы магнитной системы.

Исходные данные:

толщина скобы a = 0.003 м;

ширина скобы b = 0,0155 м;

постоянная часть нерабочего воздушного зазора Δ = 0,00005 м.

Нерабочий зазор состоит из изменяющейся части, зависящей от величины рабочего зазора и постоянной части, обусловленной немагнитной прокладкой: (3.2.2)

где δ_н^’- изменяющаяся часть нерабочего зазора, м.

(3.2.3)

В соответствии с принятыми значениями рабочего воздушного зазора рассчитаем значения нерабочего воздушного зазора по (3.2.2), его магнитную проводимость по (3.2.1) и магнитное сопротивление по (3.1.2).

при δ_р1=0,5 ·10^-3м:

.

при δ_р2=1,0 ·10^-3м:

.

при δ_р3=1,5 ·10^-3м:

.

Результаты расчетов приведены в таблице 2:

Таблица 2

dp×10-3,м	0.5	1.0	1.5
d’нз×10-3,м	0,1026	0,1553	0,2079
Gн×10-7, Гн	5,69	3,761	2,809
Rн×107, Гн	0,176	0,2659	0,356

Рассчитаем магнитную проводимость нерабочего воздушного зазора между прямоугольной скобой и основанием цилиндрического сердечника (зазор обусловлен наличием немагнитного покрытия этих деталей и неплотностью их прилегания). Магнитную проводимость рассчитаем без учета краевых потоков по формуле (3.2.4).

(3.2.4).

Исходные данные:

примем зазор равным δ_н1=15·10^-6м;

диаметр сердечника d_с=9 ·10^-3м.

.

Магнитное сопротивление этого зазора:

.

Расчет проводимости зазора утечки

Рассчитаем магнитную проводимость зазора утечки, образованного параллельными цилиндрическим сердечником и прямоугольной скобой (рисунок 3).

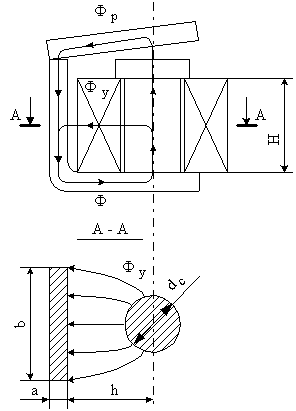
Рисунок 3. Упрошенное изображение магнитного поля

Магнитный поток утечки (рассеивания) замыкается помимо рабочего воздушного зазора. Потоки рассеяния являются распределенными и замыкаются внутри контура магнитопровода и вне его. При расчете будем учитывать только магнитные потоки, замыкающиеся внутри контура магнитопровода. Примем высоту зоны рассеяния равной высоте катушки электромагнита.

Удельная магнитная проводимость зазора утечки определяется по формуле (3.3.1).

(3.3.1),

гдеK=0.87 - коэффициент, зависящий от соотношения b и h.

(3.3.2).

Полная проводимость зазора утечки:

(3.3.3),

гдеH – высота катушки, м.

Приведенную магнитную проводимость воздушного зазора для потока рассеяния определим по формуле (3.3.4).

(3.3.4).

Исходя из вышеприведенных формул, определим удельную и приведенную магнитную проводимость зазора утечки.

Исходные данные:

расстояние от сердечника до прямоугольной скобы h=11,25 ·10^-3м;

высота катушки H=47 ·10^-3м.

,

,

,

.

Приведенное магнитное сопротивление зазора утечки:

.

Расчет коэффициентов рассеяния тока

Коэффициент σ рассеяния потока определяется через магнитные проводимости по формуле (3.4.1).

(3.4.1).

Подставим в (3.4.1) значения проводимостей рабочего и нерабочего зазоров и проводимость утечки:

,

,

.

Результаты расчетов приведены в таблице 3

	0,5	1,0	1,5
	1,322	1,592	1,732