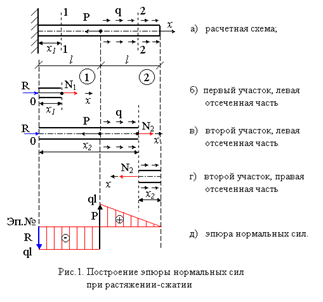
Задача С 1
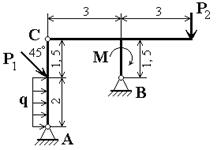
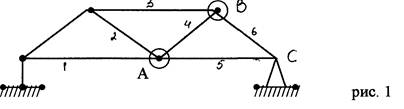
Жестяная рама закреплена в точке А шарнирно, а в точке В прикреплена к шарнирной опоре на катках. На раму действуют пара сил с моментом М = 100H*м и две силы F1 = 10H под углом 30° к горизонтальной оси, приложенная к точке K, и F4=40H под углом 60° к горизонтальной оси, приложенная к точке H.
Определить реакции связей в точках A и В, вызываемые заданными нагрузками. При окончательных подсчетах принять l = 0,5 м
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 2 l l
2 l l
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Дано: XAF4’X
Дано: XAF4’X
М = 100 Н * м A H
![]()
![]()
![]()
![]()
![]()
![]() F 1 = 10 Н F4’’ F4 F1’’F1 l
F 1 = 10 Н F4’’ F4 F1’’F1 l
![]()
![]()
![]()
![]() £ 1= 30° K
£ 1= 30° K
![]()
![]() F 4 = 40 HF1’
F 4 = 40 HF1’
![]() L = 0,5 м М 3l
L = 0,5 м М 3l
£ 4 = 60° 2l
![]()
![]()
![]()
![]()
![]() RB
RB
![]()
![]() XА, YА, RBД
XА, YА, RBД
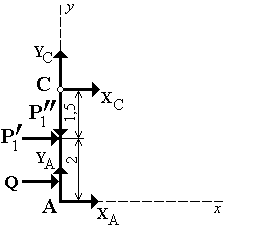
Рис. С 1.0.
Решение:
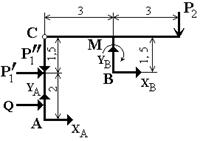
Рассмотрим равновесие рамы. Проведем координатные оси XY (начало координат в точке А). На раму действуют следующие силы: ![]() 1 и
1 и ![]() 4, пара сил моментом М и реакция связи
4, пара сил моментом М и реакция связи ![]() A,
A, ![]() A,
A, ![]() B (реакция неподвижной шарнирной опоры А изображаем двумя ее составляющими, реакция шарнирной опоры на катках направлена перпендикулярно опорной плоскости).
B (реакция неподвижной шарнирной опоры А изображаем двумя ее составляющими, реакция шарнирной опоры на катках направлена перпендикулярно опорной плоскости).
Составляем три уравнения равновесия:
1) ∑ FKX=0; XA+F4*coς 60 °+ F1*coς 30 °=0
2) ∑ FKY=0; YA-F4*ςin 60 °+ F1* ςin 30 °+RB=0
3) ∑ MA (FK)=0; -F4*ςin 60 °*2l+ F1* ςin 30 °*3l+F1* coς 30 °*l-M+RB*5l=0
Из уравнений (1) находим XA:
XA= -F4* coς 60 °-F1* coς 30 °= -40*0,5-10*0,866= -28,66H
Из уравнения (3) находим RB:
RB=![]() =
=
=![]() =
=
![]() =49,12H
=49,12H
Из уравнения (2) находим YA:
YA=
![]()
Проверка:
![]()
![]()
![]()
ð все силы реакции найдены правильно:
Ответ:
![]()
![]()
![]()
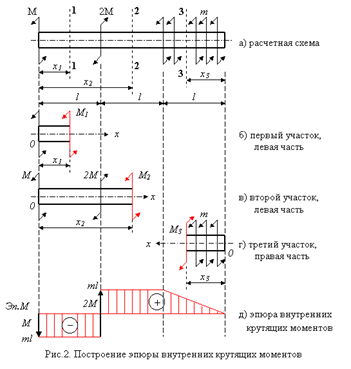
Задача С 2
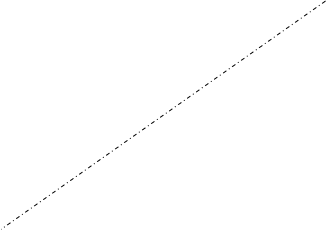
Однородная прямоугольная плита весом P=5kH со стороны АВ=3l, ВС=2l закреплена в точке А сферическим шарниром, а в точке В цилиндрическим шарниром (подшипником) и удерживается в равновесии невесомым стержнем СС! На плиту действуют пара сил с моментом М=6лН*м, лежащая в плоскости плиты, и две силы. Значения этих сил, их направления и точки приложения Н, £1=90°с, Д, £2=30°с; при этом силы ![]() и
и ![]() лежат в плоскостях, параллельных плоскости xy, сила
лежат в плоскостях, параллельных плоскости xy, сила![]() - в плоскости, параллельной xz, сила
- в плоскости, параллельной xz, сила ![]() - в плоскости параллельной yz. Точки приложения Д и Н находятся в серединах сторон плиты. Определить реакции связей в(.) А и В, С. При окончательных расчетах принять l=0,5м.
- в плоскости параллельной yz. Точки приложения Д и Н находятся в серединах сторон плиты. Определить реакции связей в(.) А и В, С. При окончательных расчетах принять l=0,5м.
![]() С1
С1
![]()
![]()
![]()
 Z
Z
![]() Дано:
Дано:
![]()
![]()
![]()
![]()
![]()
![]()

![]()


![]()
![]()
![]()
![]()
![]()
![]()

![]()
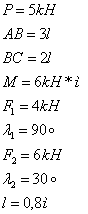
![]() Y
Y
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
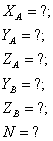
Рис С 2.0.
Решение:
1) Рассмотрим равновесие плиты. На нее действуют заданные силы: ![]() пара сил с моментом М, а также реакции связей. Реакцию сферического шарнира разложим на 3 составляющие:
пара сил с моментом М, а также реакции связей. Реакцию сферического шарнира разложим на 3 составляющие: ![]() цилиндрического шарнира (подшипника) - на две составляющие:
цилиндрического шарнира (подшипника) - на две составляющие: ![]() (в плоскости перпендикулярной оси подшипника), реакцию
(в плоскости перпендикулярной оси подшипника), реакцию ![]() стержня направим вдоль стержня, предполагая, что он растянут (рис. С 2.0.)
стержня направим вдоль стержня, предполагая, что он растянут (рис. С 2.0.)
2) Для определения ![]() составляем равновесия, действующей на плиту пространственной системы сил:
составляем равновесия, действующей на плиту пространственной системы сил:
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
Из уравнения (4) находим N:
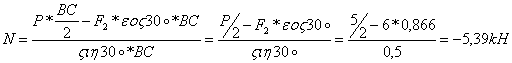
Из уравнения (5) находим ZB:
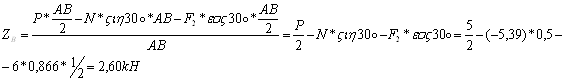
Из уравнения (1) находим XA:
![]()
Из уравнения (6) находим YB^
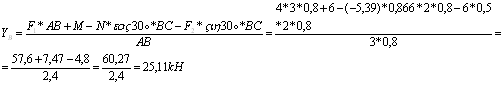
Из уравнения (2) находим YA:
![]()
Из уравнения (3) находим ZA:
![]()
Ответ:
XA= -1,67kH
YA= -29,11kH
ZA= -0,10kH
YB=25,11kH
ZB=2,60kH
N= -5,39kH
Знаки указывают, что силы ![]() направлены противоположно показанным на рис. С 2.0.
направлены противоположно показанным на рис. С 2.0.
Задача К1
![]() Дано:
Дано:
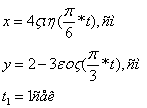
![]() Три движения точки на плоскости
Три движения точки на плоскости
Найти:
![]() - уравнение траектории точки
- уравнение траектории точки
![]() для момента времени
для момента времени
![]()
![]() y
y
B

![]()
x
Рис. К 1.0.
Решение:
1) Для определения уравнения траектории исключим из заданных уравнений движения время t:
![]() (1)
(1)
Преобразуя систему (1), получим:
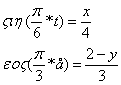 (2)
(2)
Поскольку время е входит в аргументы тригометрических функций, где один аргумент вдвое больше другого, используем формулу: ![]() то есть:
то есть:
![]()
Итак, получаем:
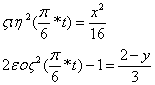 (3)
(3)
Преобразуя систему (3), получим:
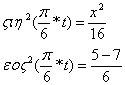 (4)
(4)
Преобразуем: ![]()
Упрощая выражение, получим:
![]()
![]() (5)
(5)
Выражение (5) – это уравнение траектории точки. График – парабола с вершиной в точке (0;11) на рис. К.1.0 а
2) Скорость точки найдем по ее траектории на координатной оси:
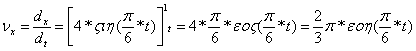 см/с
см/с
![]() y
y
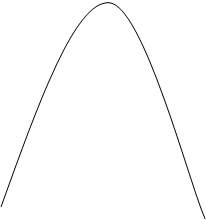 (0;11)
(0;11)
y=-0,375x2+11
![]()
(-5,4;0) (5,4;0)
![]() x
x
Рис. К 1.0 а
При t=1 сек, находим ![]()
![]()
![]()
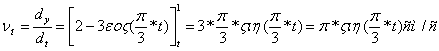
При t=t1=1 сек, находим ![]()
![]()
Находим скорость точки:
![]()
3) Аналогично найдем уравнение точки:
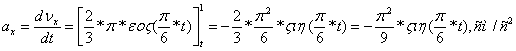
При t=t1=1 сек, находим
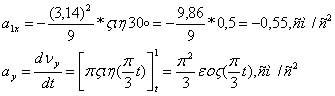
При t=t1=1 сек, находим:
![]()
Находим ускорение точки:
![]()
Найдем касательное ускорение, дифференцируя по времени равенства:
![]()
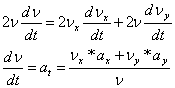
Учитывая найденные значения ![]() при t= 1 сек, получим:
при t= 1 сек, получим:
![]()
5)Нормальное ускорение определяется по формуле:
![]()
6)Радиус кривизны траектории определяется по формуле:
![]()
Ответ:
![]()
a1=1,73 см/с2
aT=1,07 см/с2
an=1,36 cм/c2
![]() =7,53 см
=7,53 см
Задача К2
Дано:
![]() l1=0,4 м
l1=0,4 м
l2=1,2 м
l3=1,4 м
l4=0,8 м
![]() =60°
=60°
![]() =60°
=60°
![]() =60°
=60°
![]() =90°
=90°
![]() =120°
=120°
![]() 4=3с-2
4=3с-2
![]() =10с-2
=10с-2
![]()
Найти:
![]() -?
-?
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]() 2
2
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
O1
4
![]()
O2
Рис. К2.0.
Решение:
1) Строим положение данного механизма в соответствии с заданными узлами (рис К2.0)
2) Определяем скорость точки ![]() по формуле:
по формуле:
![]()
Точка ![]() одновременно принадлежит стержню
одновременно принадлежит стержню ![]()
![]() . Зная
. Зная ![]() и направление
и направление ![]() воспользуемся теоремой о проекциях скоростей двух точек тела (стержня
воспользуемся теоремой о проекциях скоростей двух точек тела (стержня ![]() ) на прямую, соединяющую эти точки (прямая
) на прямую, соединяющую эти точки (прямая ![]() )
)
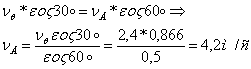
Точка В одновременно принадлежит к стержню 3 те к стержню АВ. При помощи теоремы о проекциях скоростей определяем скорость точки А:
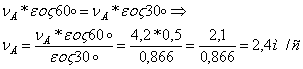
Для определения скорости точки D стержня АВ построим мгновенный центр скоростей для звенья АВ (рис. К 2.0)
Определяем угловую скорость звенья 3 по формуле:
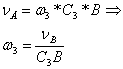
Из треугольника АС3В при помощи теоремы синусов определяем С3В:
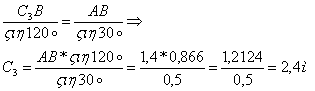
Т.О., угловая скорость стержня 3 равна:
![]()
Скорость точки D стержня АВ определяется по формуле:
![]()
С3D определяем при помощи теоремы синусов:
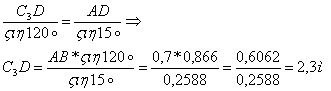
Итак: ![]() =
=![]()
Определяем ускорение точки А.
Т.к., угловая ускорение ![]() известно, то
известно, то
![]()
Найдем нормальное ускорение точки А определяем по формуле:
![]()
Ускорение точки А плоского механизма определяется по формуле:
![]()
Ответ:

Задача Д1
![]() Дано:
Дано:
m=2 кг
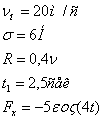
![]()
Найти:
x=f(t) – закон движения груза на участке ВС
![]()
![]()
![]()

![]()
![]()
![]()
![]()

![]()

![]()
![]()
![]()
![]() А
А
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
C ![]()
![]() В
В ![]()
![]()
![]() D
D ![]()
x 30°
![]()
Рис. D 1.0.
Решение:
1) Рассмотрим движение груза D на участке АВ, считая груз материальной точкой.
Изображаем груз (в произвольном положении) и действующее на него силы:
![]() . Проводим ось AZ в сторону движения и составляем дифференциальное уравнение движения груза в проекции на эту ось:
. Проводим ось AZ в сторону движения и составляем дифференциальное уравнение движения груза в проекции на эту ось:
![]() (1)
(1)
![]() (2)
(2)
Далее, находим:
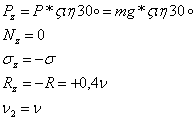 (3)
(3)
Учитывая выражение (3) в (2) получим:
![]() (4)
(4)
![]() (5)
(5)
Принимая g=10ми/с2 получим:
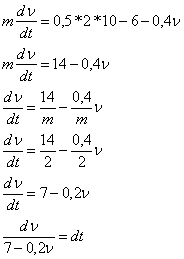
Интегрируем:
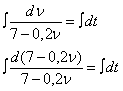

Начальные условия:
При t=0; ![]()
![]()
или
ln(7-0,2*![]() )= C1
)= C1
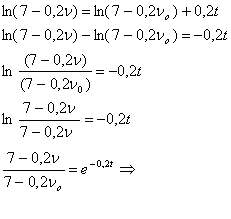
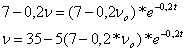
При t=t1=2,5сек, ![]() , получим:
, получим:
![]()
2) Теперь рассмотрим движение груза на участке ВС, найденная скорость ![]() будет для движения на этом участке начальной скоростью
будет для движения на этом участке начальной скоростью
![]()
Изображаем груз (в произвольном положении) и действующие на него силы:
![]() (рис. D1.0)
(рис. D1.0)
Проведем из точки В ось BX и составим дифференциальное уравнение движения груза в проекции на эту ось:
![]() (6)
(6)
Т.к., ![]() то уравнение (6) примет вид:
то уравнение (6) примет вид:
![]() (7)
(7)
Разделив обе части равенства на m=2 кг, получим
![]() (8)
(8)
![]() (9)
(9)
Умножим обе части уравнения (9) на ![]() и проинтегрируя, получим:
и проинтегрируя, получим:
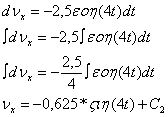
Учитывая начальные условия:
При ![]()
![]()
Т.о., ![]()
Умножим обе части равенства на dt и снова интегрируем, получим:
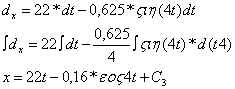
Начальные условия: при ![]()
Итак:
![]()
Ответ:
![]()
Это закон движения груза D в изогнутой трубе АВС.
Похожие работы
... сечения увеличиваются. Из-за трения между опорными плитами нагружающего устройства и торцевыми поверхностями образца он принимает бочкообразную форму. Для ряда пластичных материалов обнаружить напряжение, аналогичное временному сопротивлению при растяжении, не удается, так как образец сплющивается. Хрупкие материалы проявляют значительно лучшую способность сопротивляться деформациям сжатия, чем ...
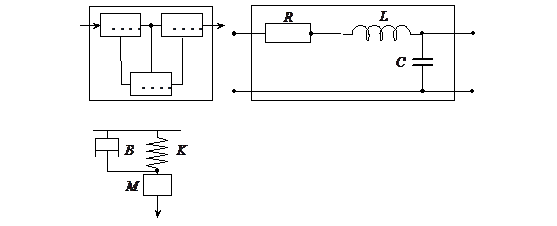
... цепи W1(s) = Wp(s) представлено как параллельное соединение простейших звеньев. 2.9 Неопределенность моделей систем управления Математические модели не отражают исчерпывающим образом динамические свойства систем управления в силу идеализации и упрощений, неизбежных при моделировании, неточной реализации алгоритмов управления и изменений характеристик объектов и других элементов в ...
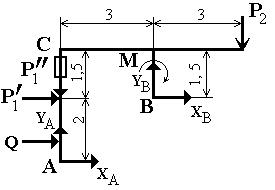
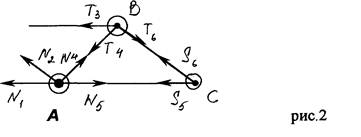
... (1) где кН. После подстановки данных и вычислений уравнение (1) получает вид: кН (1’) Второе уравнение с неизвестными и получим, рассмотрев систему уравновешивающихся сил, приложенных к части конструкции, расположенной левее шарнира С (рис. 3): Рис. 3. . Отсюда находим, что кН. Подставив найденное значение в уравнение (1’) найдем значение ...
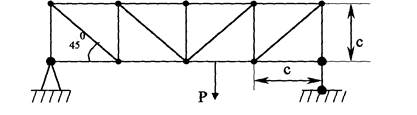
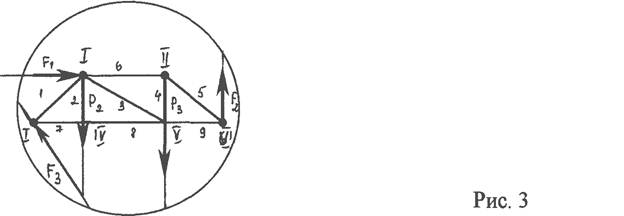
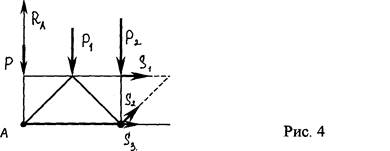
... , что стержень сжат, а не растянут. Глава 2.Расчет плоской фермы на подвижную нагрузку. Содержание главы представляет из себя решение задачи на расчет плоской фермы при подвижной нагрузке. Задача: Рассчитать на прочность (т. е. подобрать площадь сечения) стержни 1, 2, 3, определив предварительно опасное положение силы Р=50 тонн, движущейся по нижнему поясу фермы; нагрузка , при движении ...
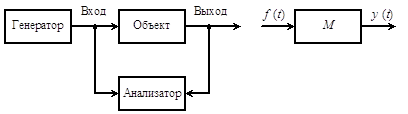

0 комментариев