Навигация
РЕФЕРАТ
на тему:”Фізика атомів і молекул”
План
1. Використання рівняння Шредінгера до атома водню. Хвильова функція. Квантові числа.
2. Енергія атома водню і його спектр. Виродження рівнів. Правила відбору.
3. Механічний і магнітний моменти атома водню.
1. Використання рівняння Шредінгера до атома водню. Хвильова
функція. Квантові числа
Теорія Бора будови й властивостей енергетичних рівнів електронів у водневоподібних системах знайшла своє підтвердження у квантовій механіці. Квантова механіка також стверджує, що:
a) електрони в атомах водню знаходяться лише в дискретних енергетичних станах. При переході електронів з одних станів в інші випромінюється або поглинається фотон;
б) не існує певних колових орбіт електронів. В силу хвильової природи електрони «розмиті» в просторі подібно до хмарки негативного заряду. Розміри й форму такої хмарки в заданому стані можна розрахувати.
Розглянемо рух електрона в кулонівському полі ядра із зарядом Ze, потенціальна енергія якого виражається формулою
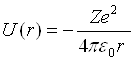 , (1)
, (1)
де r – відстань між електроном і ядром.
Стан електрона в атомі водню або водневоподібному атомі описується деякою хвильовою функцією , яка задовольняє стаціонарне рівняння Шредінгера:
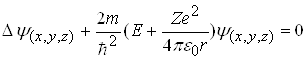 , (2)
, (2)
де 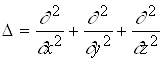 ― оператор Лапласа; Е ― значення повної енергії електрона в атомі; m ― маса частинки;
― оператор Лапласа; Е ― значення повної енергії електрона в атомі; m ― маса частинки; ![]()
![]() (x,y,z) ― хвильова функція у декартовій системі координат.
(x,y,z) ― хвильова функція у декартовій системі координат.
Для розв’язування рівняння Шредінгера (2), тобто знаходження виду хвильової функції для електрона в атомі водню слід перейти від декартових координат до сферичних. У цьому випадку зв’язок між параметрами цих систем координат визначається з рис. 1.12.
Співвідношення, які пов’язують координати x,y,z декартової прямокутної системи координат із сферичними координатами r, , такі:
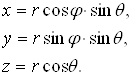 (3)
(3)
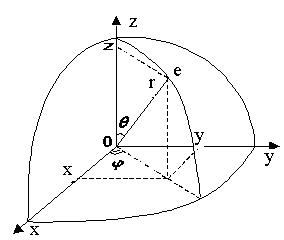
Рис. 1.
Таким чином можна вважати, що хвильова функція електрона в атомі водню залежить від сферичних координат, тобто r, .
Опустивши досить громіздкі перетворення переходу від декартової системи координат до сферичної, одержимо:
![]() . (4)
. (4)
Якщо розглядати основний (не збуджений) стан атома водню, то другою й третьою складовими в лівій частині рівняння (4) можна знехтувати. Електрон в такому стані рухається лише по коловій траєкторії і хвильова функція не залежить від і . Тому
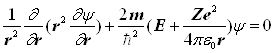 . (5)
. (5)
Хвильова функція електрона в основному стані (5) є функцією лише r, тобто r). Такий стан називається s-станом; він має сферично-симетричний характер. Імовірність виявити електрон у заданій точці атома залежатиме лише від r. Умовам стаціонарного стану відповідає центральносиметрична функція, що легко диференціюється і має вигляд:
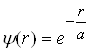 , (6)
, (6)
де a ─ деяка стала величина, яка має розмірність довжини.
Необхідні похідні від (6) підставимо в (5). Після скорочення на ![]() одержимо:
одержимо:
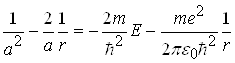 . (7)
. (7)
Рівність (7) має місце для будь-яких значень r при виконанні таких умов:
![]()
 (8)
(8)
Розв’язавши систему рівнянь (8) відносно а і Е одержуємо:
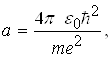 (9)
(9)
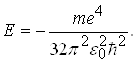 (10)
(10)
Покажемо, що вираз (9) є найбільш імовірною відстанню електрона в атомі водню до ядра. Імовірність знайти електрон на відставні r від ядра, точніше в інтервалі відстаней від r до r+dr, тобто в кульковому шарі з обємом dV=4r2 dr, дорівнює:
![]() . (11)
. (11)
З урахуванням (6), хвильової функції основного стану маємо:
![]() , (12)
, (12)
де 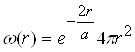 ― густина імовірності.
― густина імовірності.
Дослідимо вираз густини імовірності на максимум, тобто похідну від (r) прирівняємо до нуля
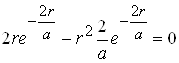 ,
,
звідки
r=a. (13)
Цей результат є окремим випадком загального висновку: борівські орбіти електрона в атомі водню є геометричними місцями точок, у яких із найбільшою імовірністю можна виявити електрон.
Залежність густини імовірності (r) виявлення електрона на різних відстанях від ядра показана на рис. 2.
За теорією Бора імовірність виявлення електрона у стані з n=1 відмінна від нуля лише для r=a, а згідно з висновками квантової механіки ця відстань є лише найбільш імовірною.
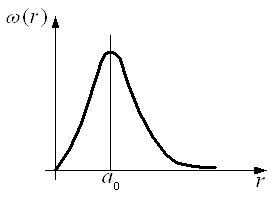
Рис. 2
Теорія Бора дає можливість визначити значення енергії електрона в будь-якому енергетичному стані, а також радіус відповідних борівських орбіт:
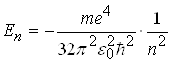 , (14)
, (14)
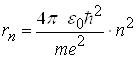 , (15)
, (15)
де m ― маса електрона; e ― заряд електрона; 0 ― діелектрична проникність вакууму; ![]() ― стала Планка, поділена на 2; n=1,2,3,...─ головні квантові числа.
― стала Планка, поділена на 2; n=1,2,3,...─ головні квантові числа.
Зіставлення (9) і (15), а також (10) і (14) показують, що висновки квантової механіки й теорії Бора повністю збігаються. Цей збіг підкреслює значну історичну роль теорії Бора, яка ще не є квантовою, однак і не класичною теорією.
Хвильові функції для наступних основних двох енергетичних рівнів електронів у атомі водню мають вигляд
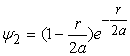 , (16)
, (16)
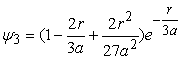 . (17)
. (17)
Ці хвильові функції також є розвязками рівняння (5) при умові, що ![]() і
і ![]() . Можна показати, що формула (14) є значенням енергії електрона на будь-якому енергетичному рівні. Однак для повного пояснення стану електрона в атомі водню необхідні ще два квантові числа, які входять у відповідні рівняння хвильових функцій і які характеризують момент імпульсу електрона в атомі.
. Можна показати, що формула (14) є значенням енергії електрона на будь-якому енергетичному рівні. Однак для повного пояснення стану електрона в атомі водню необхідні ще два квантові числа, які входять у відповідні рівняння хвильових функцій і які характеризують момент імпульсу електрона в атомі.
Для збуджених атомів хвильові функції не є центрально симетричними і залежать не лише від r, а й від і . Ці хвильові функції містять три цілочислові параметри, які називають квантовими числами. Серед них:
n ― головне квантове число, квантує енергію електрона – збігається з аналогічним квантовим числом теорії Бора і набуває значень від 1 до ;
l ― орбітальне квантове число, квантує момент імпульсу
![]() . (18)
. (18)
Орбітальне квантове число набуває значень l=0,1,2,... .
ml― магнітне квантове число, квантує проекцію орбітального моменту імпульсу на вісь Z напрямку зовнішнього магнітного поля
![]() . (19)
. (19)
Магнітне квантове число набуває значень ml= 0,±1,±2,±3,... .
Похожие работы
... для систем, частинок з антисиметричними хвильовими функціями, тобто до ферміонів. 2.2.3. Розподіл електронів за станами. Періодична система елементів. Сукупність електронів, які перебувають у всіх можливих станах з однаковим значенням головного квантового числа n, утворює електронну оболонку (електронний шар). Енергетичні шари прийнято позначати великими латинськими літерами відповідно до ...
... універсальних законів колишньої фізики стала широко застосовувати статистичні закони й імовірнісні методи дослідження. Подальший розвиток концепції атомізму Після того, коли фізики встановили, що атом не є останньою цеглинкою світобудови й сам він побудований з більше простих, елементарних часток, ідея пошуку таких часток зайняла головне місце в їхніх дослідженнях. Як і раніше думка фізиків ...
... ї й експериментальної фізики, раніше розроблені для вивчення макромолекул небіологічного походження. Неможливо провести границю між молекулярною біофізикою і біофізичною хімією, так само як не можна провести границю між молекулярною фізикою і фізичною хімією. Класифікація областей знання має завжди історичний і не строго визначений характер. Молекулярна фізика і відповідні розділи фізичної хімії ...
... а потім дві незалежні частоти. Хаотичний режим, що характеризується суцільним спектром, з'являвся відразу слідом за квазіперіодичною двохчастотною течією. Розділ 5. Застосування понять фізики відкритих систем до моделювання обробки інформації. Знання основних закономірностей утворення структур в активних середовищах, а також у мережах, що складаються з великої кількості активних елементів, ...

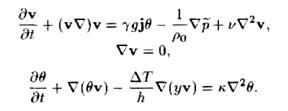
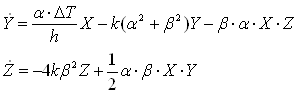
0 комментариев