Навигация
Поток напряженности электрического поля. Теорема Гаусса в интегральной форме
24053
знака
1
таблица
7
изображений
3 Поток напряженности электрического поля. Теорема Гаусса в интегральной форме
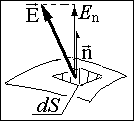
Пусть n – единичная нормаль к площадке dS (достаточно малой, чтобы пренебречь изменением электрической напряженности Е в пределах площадки). Поток dФэ электрической напряженности через эту площадку определяется как произведение нормальной компоненты Е и dS:
. (1.3.1)
Знак потока dFэ, очевидно, зависит от взаимной ориентации нормали и напряженности. Если эти два вектора образуют острый угол, поток положителен, если тупой – отрицателен.
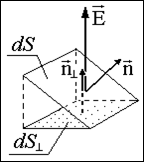
Поток dFэ через площадку, наклонную к силовой линии (т.е. к вектору Е), равен также потоку через проекцию этой площадки на плоскость, перпендикулярную силовой линии (см. рис. 1.3.2):
. (1.3.2)
Это равенство (1.3.1) следует из определения (1.3.1) для dF э и теоремы об углах с взаимно перпендикулярными сторонами.
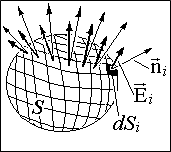
Поток Fэ электрической напряженности Е через замкнутую поверхность S (рис. 1.3.3) определяется как сумма элементарных потоков через все площадки поверхности. В пределе, когда количество площадок N стремится к бесконечности, сумма потоков через площадки переходит в поверхностный интеграл от нормальной компоненты напряженности En:
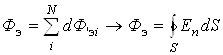. (1.3.3.)
К. Гауссом в 1844 доказана теорема (теорема Гаусса в интегральной форме), устанавливающая связь источников поля и потока напряженности через произвольную поверхность, окружающую источники.
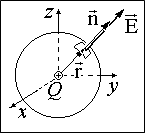
Для доказательства выведем вспомогательную формулу. Поток от точечного заряда через произвольную окружающую его сферу.
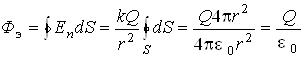. (1.3.4)
Силовые линии поля точечного заряда перпендикулярны поверхности концентрической сферы (см. рис 1.3.4). С учетом этого факта формула (1.3.4) выводится из выражения для поля точечного заряда (1.2.3). Как видно, в этом случае поток F э не зависит от радиуса сферы, а зависит только от Q .
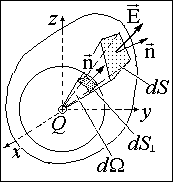
Из (1.3.2) и (1.3.4) следует, что поток поля точечного заряда через любую поверхность, окружающую заряд, равен потоку через сферу произвольного радиуса, концентричную заряду. Действительно, поток поля точечного заряда через любую площадку dS, вырезанную телесным углом dW из произвольной поверхности, получается таким же, как поток через площадку 
сферы, вырезанную тем же телесным углом. Поток поля Fэ через сферу, как уже отмечалось, не зависит от ее радиуса. Поэтому поток напряженности поля точечного заряда через поверхность S (см. рис. 1.3.5) задается формулой (1.3.4). Из формулы (1.3.4) и принципа суперпозиции следует теорема Гаусса в интегральной форме: полный поток Fэ напряженности электрического поля через произвольную замкнутую поверхность, внутри которой находится как угодно распределенный (объемный, поверхностный и т.д.) заряд Q, вычисляется по формуле
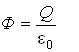. (1.3.5)
При применении теоремы Гаусса для решения задач, необходимо помнить, что в уравнении (1.3.5) Q – сумма всех зарядов внутри мысленной поверхности, через которую вычисляется поток, в том числе зарядов, принадлежащим атомам и молекулам среды (так называемых связанных зарядов).
Поток напряженности поля Е через любую замкнутую поверхность, внутри которой полный заряд равен нулю, также равен нулю.
Похожие работы
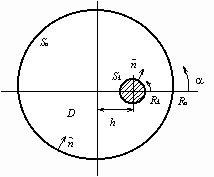
... тока от двух переменных: поляризации и скорости изменения потенциала. Данный подход дает возможность моделирования нестационарных электрических полей в электрохимических системах. Математическая модель Рассматривается заполненная проводящей средой область D, граница которой S состоит из анодных Sa, катодных Sk и изолированных Si участков: S=Sa Sc Si, =D S, Зависимость ...
... вдвое. Опыт показывает, что и сила взаимодействия уменьшается вдвое. Повторяя подобный прием, можно убедиться, что сила пропорциональна произведению зарядов. Электрическое поле Как же осуществляется взаимодействие двух зарядов? Первоначально полагали, что заряды непосредственно через пустоту действуют друг на друга. Каждый заряд на расстоянии «чувствует» присутствие другого. Это была так ...
... его реализацию. 1. НОРМИРОВАНИЕ ЭЛЕКТРИЧЕСКИХ ПОЛЕЙ В настоящее время на международном уровне и в ряде экономически развитых странах, в том числе и в нашей, разработаны и утверждены документы, регламентирующие уровни электрических полей, создаваемых высоковольтным оборудованием и сооружениями. Первые нормы по электромагнитным полям были установлены в [1, 2, 3, 4, 5]. В России регламентируются ...
... участием отрицательных ионов в процессе медленного окисления. Суммируя всё вышеизложенное, следует указать, что две основные точки зрения на механизм воздействия электрического поля на процесс горения(воздействие на газодинамику процесса или прямое воздействие на кинетику реакции) являются отражением двух более общих концепций относительно роли и места заряжённых частиц в процессе горения, одна ...
0 комментариев