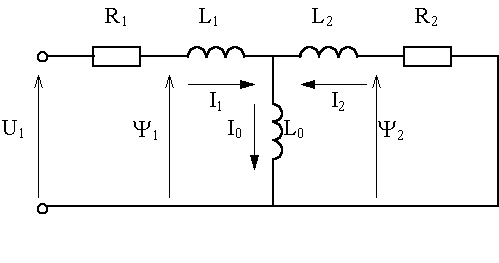
1.Исходные данные
Мощность АД, Pn (кВт) - 18,5
Число пар полюсов P=2
К.П.Д. η (%) - 89,5
сosφ - 0.88
Номинальное скольжение Sn(%) - 2,2
Номинальная частота f1(Гц) - 50
Unф (В) - 220
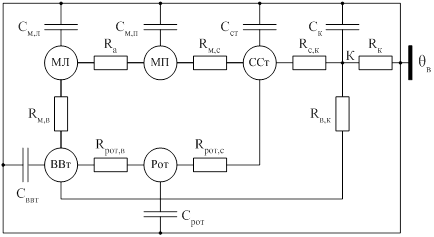
Параметры Т-образной схемы замещения двигателя (в относительных единицах):
Активное сопротивление обмотки статора Rs= 0,042
Индуктивное сопротивление рассеяния
обмотки статораХs=0,085
Приведенное активное сопротивление обмотки
ротораRr’= 0,024
Приведенное индуктивное сопротивление
рассеяния обмотки ротораХr’=0,13
Индуктивное сопротивление магнитной
цепи (сопротивление взаимоиндукции)Хm=4,3
Напряжение сети 380 В
2.Обработка исходных данных
1.Угловая скорость вращения магнитного поля
w0=2p×f1/р=6,28*50/2=157 рад/с.
Номинальная угловая скорость ротора определяется на основе выражения скольжения
Sн=(w0-wн)/w0
Откуда:
![]()
![]()
2. Пересчитаем параметры обмоток из относительных единиц в абсолютные:
![]() (Вт);
(Вт);
![]() (А);
(А);
![]() (Ом)
(Ом)
Умножим на Zn все параметры схемы замещения:
R1=R1`Zn=0,2596Ом R2=R2``Zn=0,148358 (Ом);
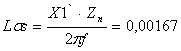 (Гн);
(Гн);
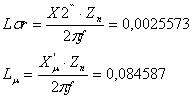 (Гн);
(Гн);
3. Разработка модели
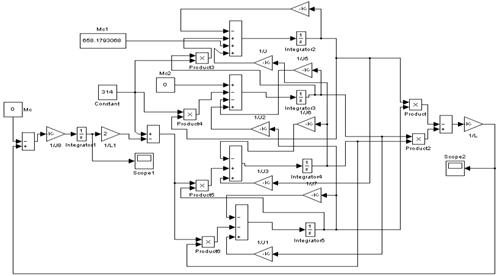
Математическая модель асинхронного двигателя в форме Коши (в системе координат u-v) имеет следующий вид:

Пуск двигателя будем выполнять на холостом ходу, и после выхода АД на синхронную скорость нагрузим номинальным моментом.
Момент инерции привода подобран таким образом, чтобы в динамической кривой скорости вращения двигателя ω (t) не было колебаний при выходе на установившийся режим.
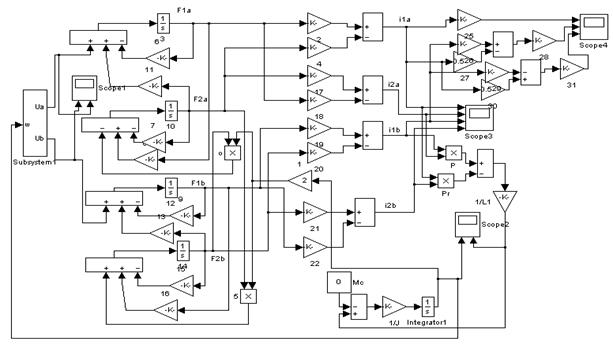
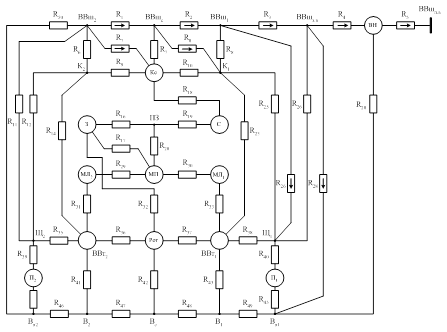
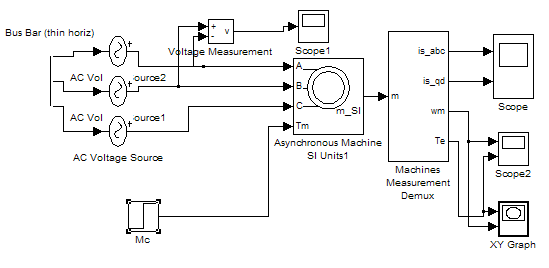
Блок-схема прямого пуска асинхронного двигателя с использованием пакета Power System Blockset
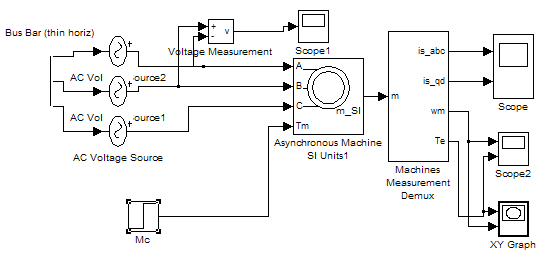
Схема прямого пуска асинхронного двигателя в осях XY.
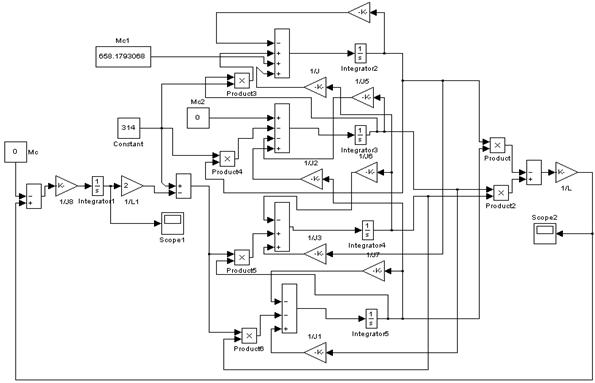
Схема прямого пуска асинхронного двигателя в осях ![]() .
.
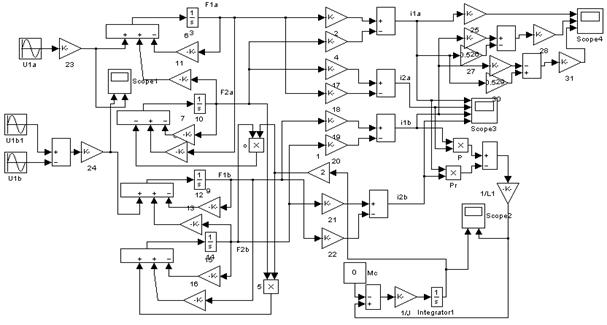
4. Результаты моделирования
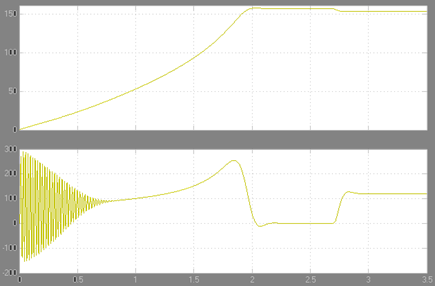
В результате моделирования нами получены следующие зависимости угловой скорости вращения якоря и момента:
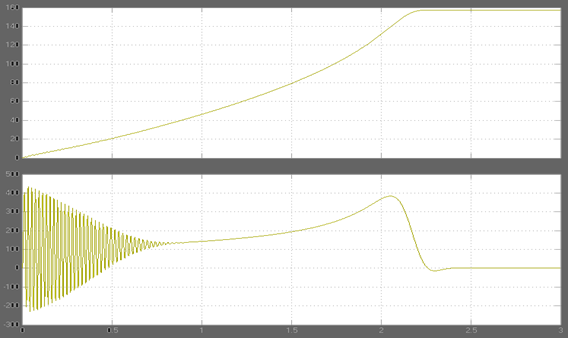
Зависимость тока статора от времени в неподвижной (связанной со статором) системе координат имеет следующий вид (для фазы А):
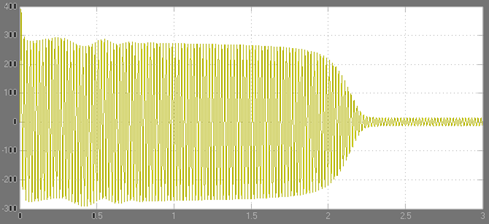
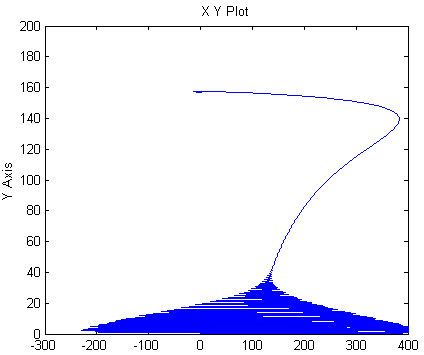
График зависимости w=f(M) имеет следующий вид:
Зависимость тока ротора от времени в вращающейся со скоростью ротора (связанной с ротором) системе координат имеет следующий вид (d q):
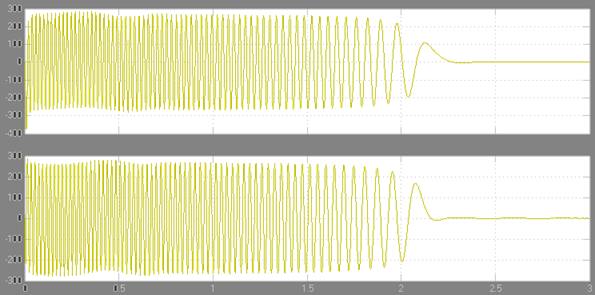
Проведём анализ адекватности разработанной нами модели прямого пуска асинхронного двигателя на на основе расчета процентного совпадения параметров номинального режима, полученных при моделировании и рассчитанных по справочным данным.
В установившемся режиме при нагрузке на валу двигателя, соответствующей номинальной, значение угловой скорости будет равно:
![]()
В результате моделирования получено значение:
![]()
Определим расхождение сравниваемых параметров в процентах:
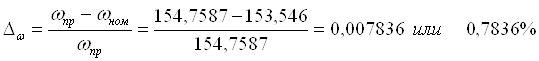
Значение момента на валу двигателя будет равно:
![]()
В результате моделирования получено значение:
![]()
Определим расхождение сравниваемых параметров в процентах:
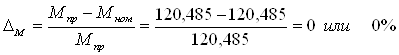
Такое расхождение результатов моделирования и номинальных данных двигателя даёт основание полагать, что разработанная нами модель адекватно отражает прямой пуск реального асинхронного двигателя.
По результатам моделирования определить номинальный ток, номинальную скорость, ток холостого хода, пусковой ток, кратность пускового тока, кратность пускового момента.
Номинальный ток равен Iном=38 А
Номинальная угловая скорость ![]()
Ток холостого хода Iх.х.=13,9А
Пусковой ток Iп=390,5А
Кратность пускового тока
![]()
Кратность пускового момента
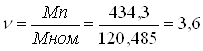
Вывод: при выполнении курсовой работы я познакомился с методом моделирования прямого пуска АД с короткозамкнутым ротором на основе обобщённой машины.
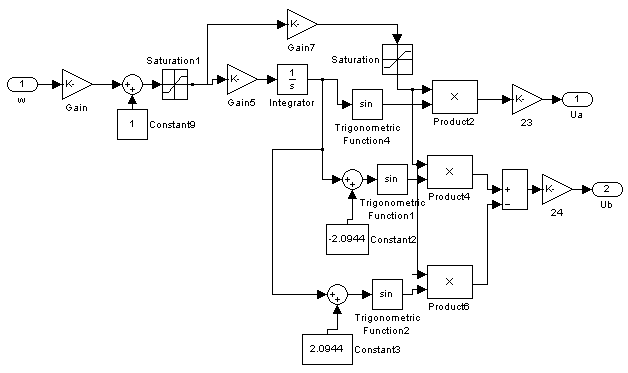
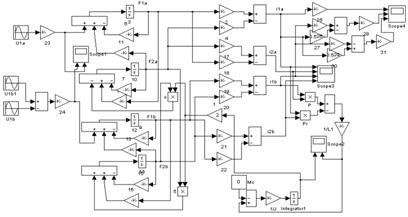
Схема частотного пуска асинхронного двигателя.
Результаты моделирования
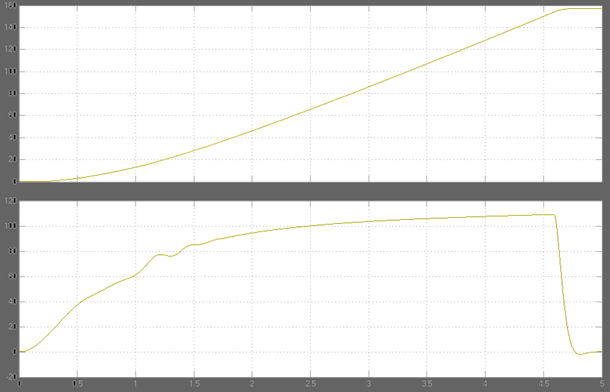
Зависимость угловой скорости ротора и величины электромагнитного момента от времени:
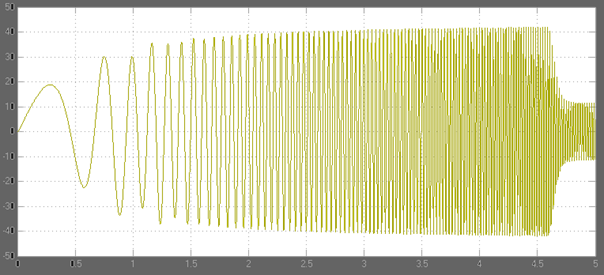
Зависимость тока статора от времени в неподвижной (связанной со статором) системе координат имеет следующий вид (для фазы А):
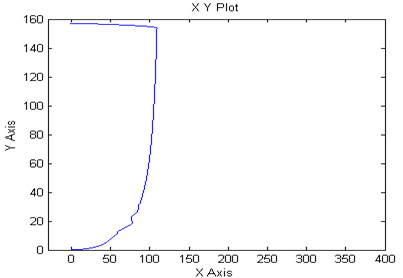
Зависимость угловой скорости ротора от величины электромагнитного момента имеет следующий вид:
Напряжение питания фазы А.
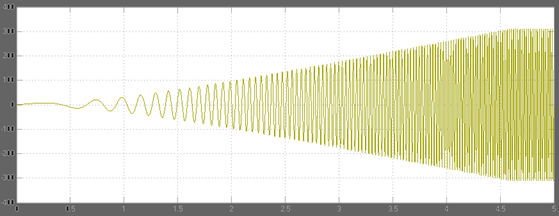
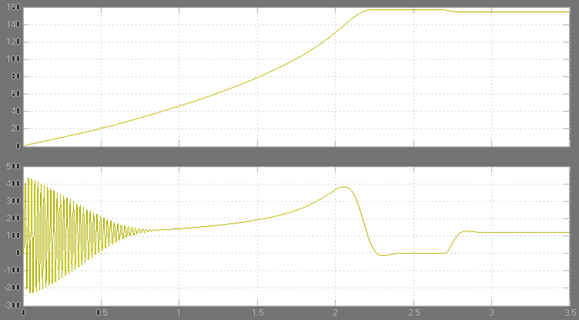
С увеличением величины абсолютного скольжения уменьшается время переходного процесса, но более резко выражены пусковые броски момента и возрастает пусковой ток. А с уменьшением величины абсолютного скольжения увеличивается время переходного процесса, соответствующего пуску, и практически отсутствуют пусковые броски момента и пускового тока.
Похожие работы
... тепловой схемы выполнялось для стационарного режима, так как коэффициенты теплоотдачи в переходном и стационарном режимах одинаковы. Полученные результаты используются в компьютерной лабораторной работе «Моделирование нагрева асинхронного двигателя в различных режимах работы». Лабораторная работа выполнена в программной среде MatLab 6.1, и в ее приложении Simulink 4. Данная работа позволяет ...
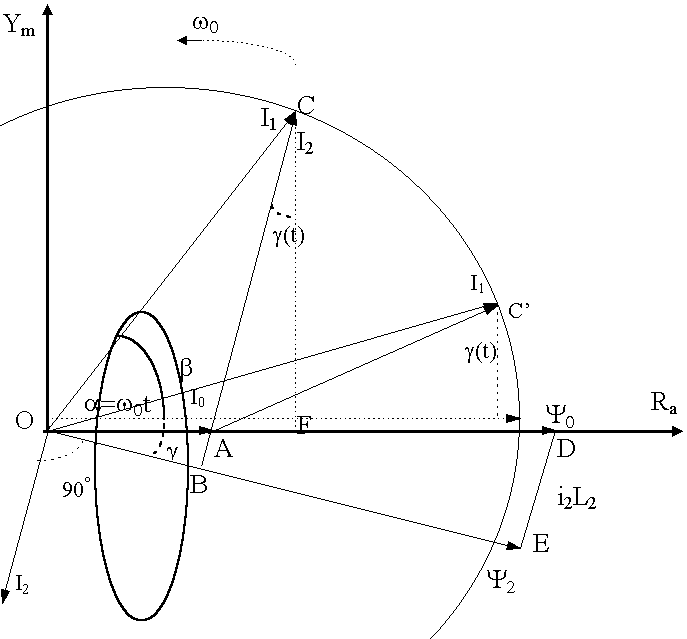
... b = a(t2) + g(t2) = w0× t + g 2. ТЕХНИЧЕСКОЕ ЗАДАНИЕ 2.1 Наименование и область применения Разрабатываемое устройство называется: автоматическая система управления асинхронным двигателем. Область применения разрабатываемого устройства не ограничивается горнодобывающей промышленностью и может использоваться на любых предприятиях для управления машинами с асинхронным приводом. 2.2 Основание для ...
... Потери, не изменяющиеся при изменении скольжения : Pст. + Pмех. = 727,12+125,6 = 852,17 Вт. Таблица 1. Рабочие характеристики асинхронного двигателя. Параметр Ед-ца Скольжение 0,005 0,01 0,015 sн=0,019 0,02 0,025 0,03 a’×r’2/s Ом 48,53 24,27 16,18 12,77 12,13 9,71 8,09 b’×r’2/s Ом 0 0 0 0 0 0 0 R = a + a¢*r¢2/s Ом 49,04 ...
... q): 5. Адекватность модели прямого пуска асинхронного двигателя Проведём анализ адекватности разработанной нами модели прямого пуска асинхронного двигателя на основе расчета процентного совпадения параметров номинального режима, полученных при моделировании и рассчитанных по справочным данным. В установившемся режиме при нагрузке на валу двигателя, соответствующей номинальной, значение ...


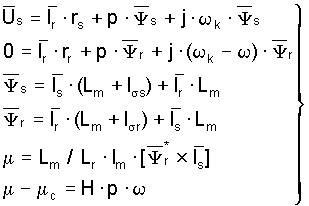
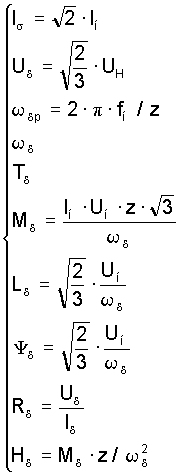
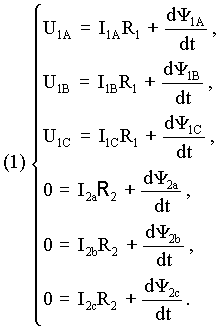

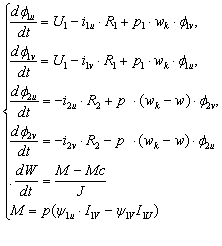
0 комментариев