МОиН Украины
Национальный технический университет
“Харьковский политехнический институт”
Кафедра электрических станций
Расчётное задание
по курсу: “Математическое моделирование”
на тему: “Модель синхронного генератора в фазных координатах”
Выполнил: ст. гр. Э-51аАбашкина О.С.
Сербиненко М.С.
Бабенков А.А.
Шаповал О.
Проверил: доц. Пискурёв М.Ф.
Харьков 2005
Общие понятия и определения в математическом моделировании
Модель – некоторый объект, с помощью которого исследуются свойства оригинала и находящегося во взаимозначном соответствии с ним и более доступном для изучения.Моделирование – исследование свойств объекта методом изучения свойств другого объекта находящегося в определённом соответствии с первым объектом и более удобным для исследования.
Под “моделью” понимают некоторые технические устройства, процесс, схемы замещения, мысленные образы, математические формулы.
Модель должна удовлетворять 3 условиям:
1. достоверно отображать некоторые свойства оригинала подлежащие изучению;
2. должно быть определённое соответствие, т.е. правила позволяющие осуществить переход от свойств модели к оригиналу и наоборот;
3. должна быть наглядной, простой и доступной для изучения.
Виды моделей:
1) Структурная. Показывает структуру объекта и взаимную связь между элементами этого объекта;
2) Модели прямой аналогии. В них процессы совпадают с процессами оригинала.
3) Физические модели. Они имеют одну и ту же физическую природу с оригиналом.
4) Математические модели, которые имеют одинаковое математическое описание с оригиналом. Эти модели бывают аналоговые и цифровые.
Основные допущения при составлении математической модели синхронного генератора
1. Не учитывается магнитное насыщение генератора.
2. В воздушном зазоре машины действуют намагничивающие силы только первой гармоники. Следовательно, ЭДС синхронного генератора – синусоидальный.
3. Не учитываются потери на перемагничивание.
4. Считают, что обмотки статора выполнены симметрично, а ротор генератора симметричен относительно осей d и q.
5. Все демпферные обмотки по оси d заменены одной демпферной обмоткой аналогичной по оси q.
6. При исследовании электромагнитных переходных процессов не учитывают изменение вращения скорости генератора.
Математическая модель синхронного генератора в фазных координатах
При составлении этой модели, в целях упрощения, не будем учитывать демпферные обмотки. Следовательно, уравнение баланса напряжений имеет вид:
Уравнение статора: Уравнение ротора:
![]()
![]()
![]() ( 1 )
( 1 )
![]()
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() - мгновенные значения напряжений обмоток статора и ротора;
- мгновенные значения напряжений обмоток статора и ротора;
![]() ,
, ![]() ,
, ![]() ,
, ![]() - потокосцепления, связанные с соответствующими обмотками;
- потокосцепления, связанные с соответствующими обмотками;
![]() ,
, ![]() ,
, ![]() ,
, ![]() - мгновенные токи, протекающие в свободных обмотках.
- мгновенные токи, протекающие в свободных обмотках.
![]()
![]() ( 2 )
( 2 )
![]()
![]()
где ![]() и
и ![]() - индуктивности и взаимоиндуктивности соответствующих обмоток.
- индуктивности и взаимоиндуктивности соответствующих обмоток.
Система уравнений 1 после подставления в неё значений из уравнений 2 превращается в систему из 4 дифференциальных уравнений с переменными коэффициентами, т.к. практически все индуктивности и взаимоиндуктивности – переменные величины, т.е. являются функцией времени (вращение ротора генератора) за исключением индуктивной обмотки возбуждения.
![]() const
const
Эти коэффициенты оказываются непостоянными из-за электрической и магнитной несимметрии ротора генератора. Т. о. система уравнений 1 и 2 позволяет смоделировать процессы в СГ в фазных координатах в режиме ХХ.
Чтобы смоделировать СГ в нагруженном режиме или в режиме КЗ необходимо добавить систему уравнений, позволяющую найти токи в обмотках статора и ротора.
Т. о. систему уравнений 1 дополненную системой уравнений 2 и уравнениями внешней цепи генератора будут представлять собой математическую модель СГ в фазных координатах.
Реализация модели синхронного генератора в фазных координатах
С целью упрощения модели представим её в виде 9 суперблоков. Первый суперблок моделирует переменные коэффициенты в уравнения для определения потокосцепления. Суперблоки 2,3,4,5 моделируют потокосцепление, 6,7,8 - фазное напряжение, 9-й – ток в обмотках возбуждения.
Первый суперблок в свою очередь состоит из подблоков. Первые три моделируют постоянные коэффициенты ![]() ,
, ![]() ,
, ![]() ,
, ![]() ; подблоки 4 – 6 моделируют индуктивности
; подблоки 4 – 6 моделируют индуктивности ![]() ,
, ![]() ,
, ![]() ; подблоки 7 – 9 моделируют взаимоиндукцию между фазами
; подблоки 7 – 9 моделируют взаимоиндукцию между фазами ![]() ,
, ![]() ,
, ![]() ; подблоки 10 – 12 моделируют взаимоиндукцию между обмотками возбуждения и фазными обмотками статора.
; подблоки 10 – 12 моделируют взаимоиндукцию между обмотками возбуждения и фазными обмотками статора.
Порядок выполнения работы
I. Реализация первого суперблока
1. При реализации модели СГ в первую очередь необходимо смоделировать постоянные коэффициенты ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Первый подблок имеет следующую реализацию:
![]()
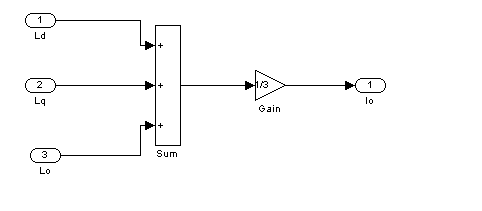
Рис.1 – Первый подблок первого суперблока, моделирующий ![]()
Реализация второго подблока:
![]()
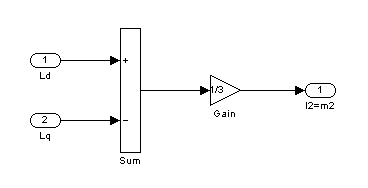
Рис.2 – Второй подблок первого суперблока, моделирующий ![]() ,
, ![]()
Реализация третьего подблока:
![]()
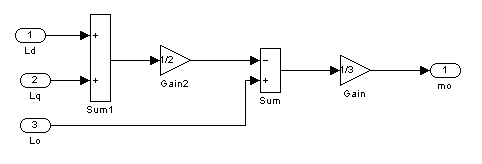
Рис.3 – Третий подблок первого суперблока, моделирующий ![]()
Каждый из трёх подблоков представляем в виде субблоков. Для этого:
а) выделяем подблок;
б) с помощью правой кнопки мыши находим операцию “Create subsystem”;
в) образуем субблок;
г) обозначаем входящие и выходящие параметры.
2. Моделирование индуктивностей ![]() ,
, ![]() ,
, ![]() :
:
![]() cos
cos![]()
![]() cos
cos![]()
![]() cos
cos![]() ,
,
где ![]() =
= ![]() ;
;
![]() - переход времени от секунд к о.е.
- переход времени от секунд к о.е.
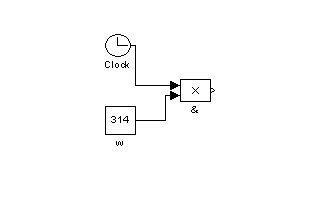
Рис. 4 – Модель ![]()
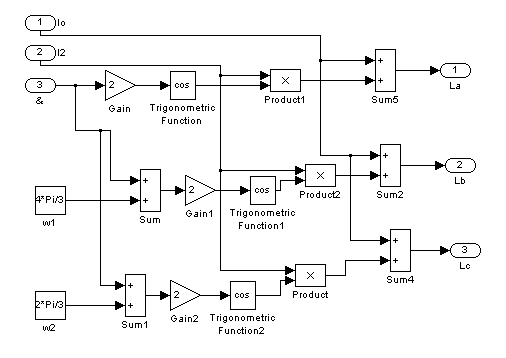
Рис. 5 – Четвертый подблок первого суперблока, моделирующий ![]() ,
, ![]() ,
, ![]()
3. Моделирование взаимоиндуктивностей между фазами ![]() ,
, ![]()
![]() cos
cos![]()
![]() cos
cos![]()
![]() cos
cos![]()
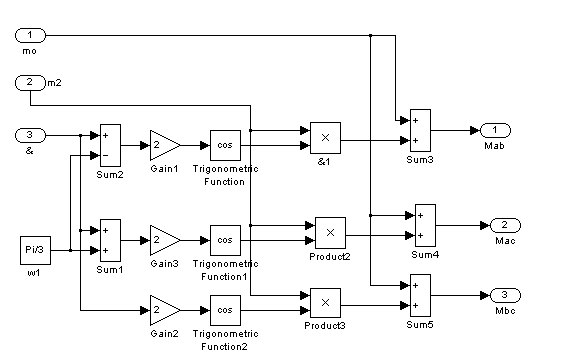
Рис. 6 – Пятый подблок первого суперблока, моделирующий ![]() ,
, ![]()
4. Моделирование взаимоиндуктивностей между обмоткой возбуждения и фазными обмотками ![]()
![]() ,
, ![]() .
.
![]() cos
cos![]()
![]() cos
cos![]()
![]() cos
cos![]()
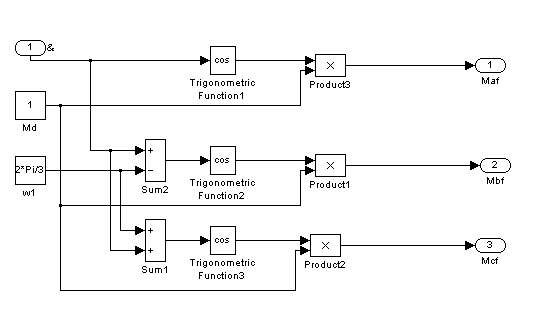
Рис. 7 – Шестой подблок первого суперблока, моделирующий ![]()
![]() ,
, ![]()
4. Каждый из подблоков преобразуем в субблок аналогично первым трём подблокам, при этом соединяя одноимённые входы и выходы подблоков.
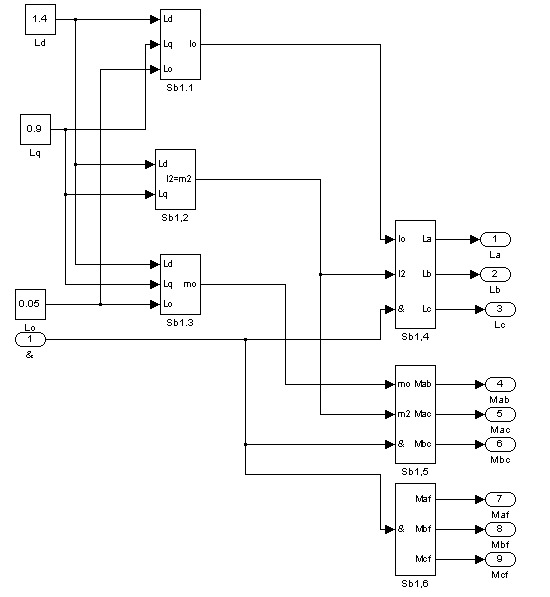
Рис. 8 – Содержимое первого суперблока
6. Образуем первый суперблок (Sb1).
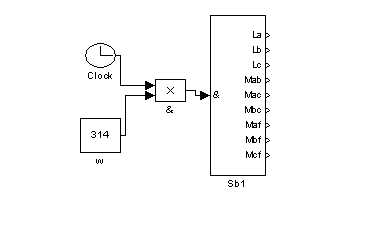
Рис. 9 – Первый суперблок (Sb1)
II. Реализация 2 - 5 суперблоков
Согласно системе уравнений (2) моделируем потокосцепления, связанные с соответствующими обмотками.
![]()
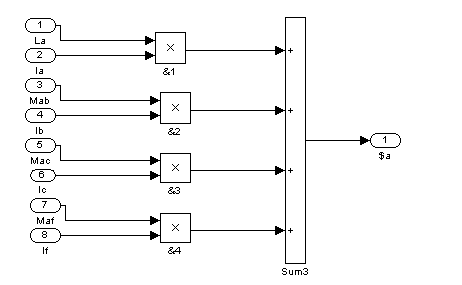
Рис. 10 – Второй суперблок (Sb2)
![]()
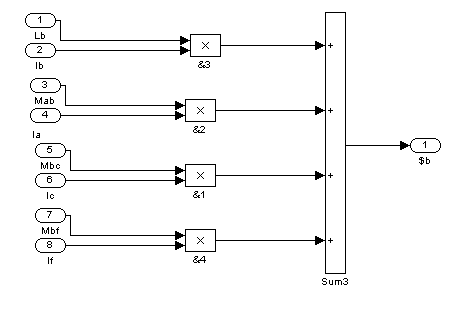
Рис. 11 – Третий суперблок (Sb3)
![]()
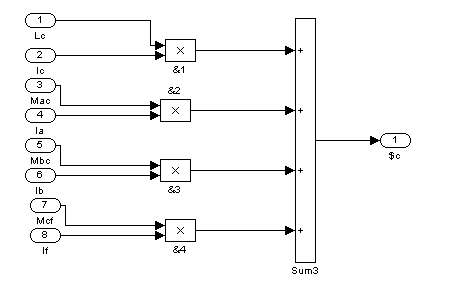
Рис. 12 – Четвертый суперблок (Sb4)
![]()
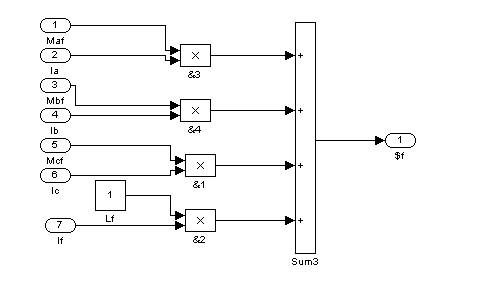
Рис. 13 – Пятый суперблок (Sb5)
Преобразуем суперблоки Sb2 - Sb5 в субблоки.
III. Реализация 6 – 8 суперблоков
Согласно системе уравнений (1) моделируем фазные напряжения в обмотках статора.![]()
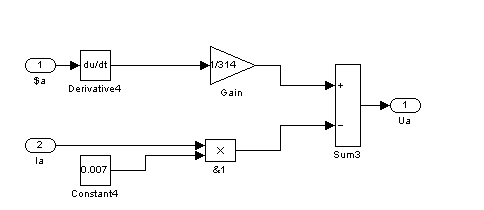
![]()
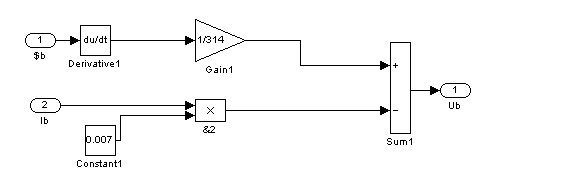
![]()
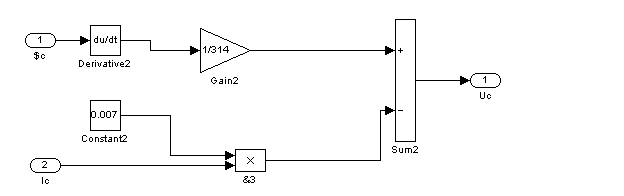
IV. Реализация девятого суперблока
Согласно той же системе уравнений (1) моделируем ток в обмотке возбуждения.
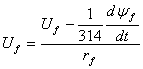
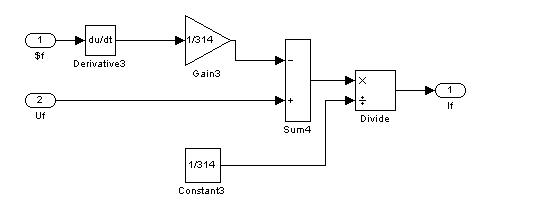
Рис. 17 – Девятый суперблок, моделирующий ток в обмотке возбуждения (Sb9)
Преобразуем каждый из суперблоков в субблоки и соединяем их одноимённые входы и выходы с предыдущими блоками. Затем аналогичным образом получим суперсуперблок (SSb), на вход которого подаём ![]() и Uf.
и Uf.
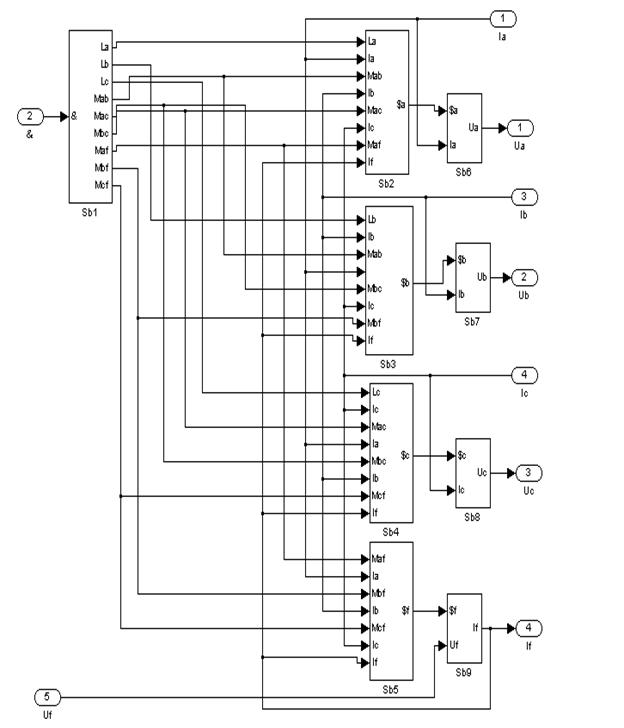
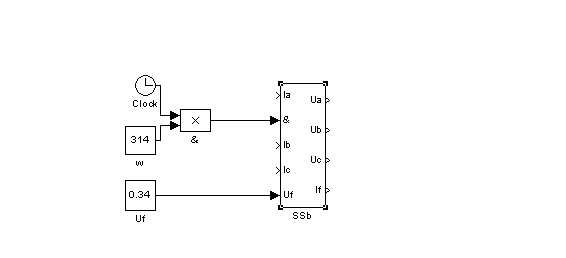
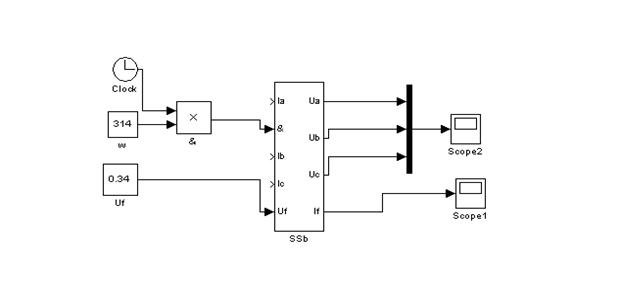
Рис. 19 – Суперсуперблок SSb
V. Модель СГ в режиме ХХ
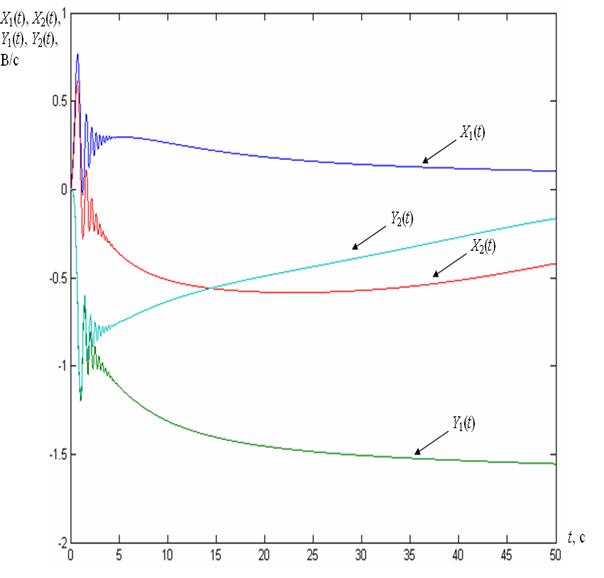
Подключив осциллографы к соответствующим выходам SSb, будем наблюдать изменение фазных напряжений и тока в обмотке возбуждения СГ в режиме ХХ. С помощью  объединяем фазные напряжения для просмотра в одной системе координат. Т.к. в данной модели фазные токи равны 0, то это модель СГ в режиме ХХ.
объединяем фазные напряжения для просмотра в одной системе координат. Т.к. в данной модели фазные токи равны 0, то это модель СГ в режиме ХХ.
Похожие работы
... випадків, аварій, а з цим і простоїв на підприємстві, укріпити та створити культуру трудової діяльності. Виконання та розробка дипломного проекту “ Розробка дослідження системи керування електроприводом змінного струму дизель-потягу з використанням нейронних мереж ” відбувається за допомогою комп'ютера, тому питання охорони праці розглядаються щодо забезпечення здорових і безпечних умов роботи ...
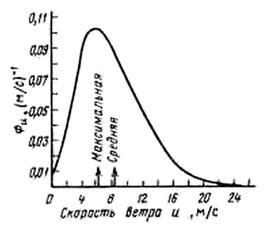
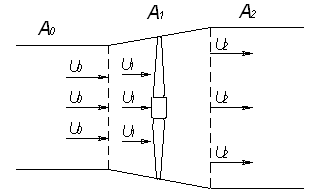
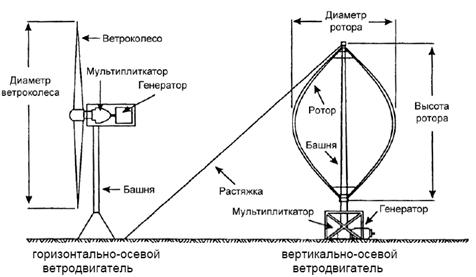
... (М) при заданных скоростях ветрового потока (ВП). При этом математическое описание параметров ВП может быть получена вероятностными методами. Рисунок 1.9 – Структурная схема ВЭУ Одним из возможных направлений разработки АЭП имитатора является его реализация на базе привода постоянного тока (рис. 1.10). Одним из достоинств ДПТ является широкое и плавное регулирование скорости вращения, ...
... . Это позволяет: -снизить трудоемкость обработки -снизить себестоимость обработки -сократить время обработки и обслуживания. Ожидаемый частный годовой экономический эффект от автоматизации шлифовального процесса путем разработки автоматической системы управления параметров станка является снижение затрат на обработку детали типа кольцо ступенчатое при годовой программе выпуска 1000 ед. ...
... концентрических окружностей с уменьшающимся радиусом по мере затухания колебаний скорости и момента. Аналогичная картина наблюдается при ступенчатом набросе нагрузки. 5. РАЗРАБОТКА ВИРТУАЛЬНОЙ ЛАБОРАТОРНОЙ РАБОТЫ НА БАЗЕ ВИРТУАЛЬНОЙ АСИНХРОННОЙ МАШИНЫ Иную возможность анализа АД представляет специализированный раздел по электротехнике Toolbox Power System Block. В его библиотеке имеются блоки ...


0 комментариев