Определение частотной дисперсии стеклянной призмы с помощью гониометра

ЛАБОРАТОРНАЯ РАБОТА N 1.2

ОПРЕДЕЛЕНИЕ ЧАСТОТНОЙ ДИСПЕРСИИ СТЕКЛЯННОЙ ПРИЗМЫ С ПОМОЩЬЮ ГОНИОМЕТРА

ЦЕЛЬ РАБОТЫ: определение спектральной зависимости коэффициента преломления стеклянной призмы и оценка ее спектральных характеристик.

1. ПРИНАДЛЕЖНОСТИ: гониометр ГС-5, стеклянная плоскопараллельная призма, ртутная лампа.

2. Электронная, классическая теория частотной дисперсии

Многие оптические явления находят удовлетворительное объяснение в предположении, что связь между векторами  и  (а также  и ) локальна во времени и пространстве. Это означало бы, что  и  определились в любой момент времени пространства  значениями  и  в тот же момент времени и при том же значении . Однако дело обстоит иначе. В ряде явлений необходимо учитывать нелокальность во времени и пространстве. К таким явлениям можно отнести частотную дисперсию диэлектрической проницаемости вещества, естественное вращение плоскости поляризации и некоторые другие. В данной работе исследуется частотная дисперсия стеклянной призмы. Рассмотрим подробнее это явление.

Будем считать, что наше поле  однородно по пространству (пространственной нелокальностью пренебрегаем), тогда для стационарного случая имеет место соотношение, определяющее связь индукции  с напряженностью электрического поля  и поляризацией среды :

.(1)

Однако наличие конечных масс электронов и ионов вещества, заряды которых определяют поляризацию , приводит к инерционности появления  для переменного поля . Следовательно, воздействие электрического поля  электромагнитной волны приведет к временной нелокальности поляризации .

В рамках линейной электродинамики поляризации среды , вызванная электрическим толчком, пропорциональна . Считая, что среда изотропна, мы запишем связь  в момент времени :

, (2)

где функция  зависит от свойств среды и от времени  с момента электрического толчка. Очевидно, что при  в силу инерционности электронов и ионов , а при  в силу наличия затухания (реальные среды диссипативны) .

Для задач, когда поле  действует достаточно долгое время (реальная электромагнитная волна), мы разбиваем весь период на достаточно малые промежутки времени, сводя задачу к последовательным электрическим толчкам. Тогда вклад в поляризацию среды в момент времени , внесенный в более ранним толчком , будет равен . В силу суперпозиции полный вектор поляризации в момент времени  определяется:

 (3)

Используя переход к новой переменной

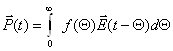.(4)

Учитывая связь (1), запишем

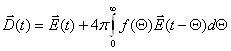. (5)

Интегрирование в (5) производится во времени, предшествующему моменту . Этого требует принцип причинности, утверждающий, что каждое событие определяется только прошедшими событиями и не может зависеть от будущих.

Для монохроматической волны  выражение (5) преобразуется:

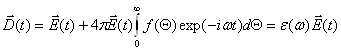,(6)

где связь между  и  записана формально в локальной форме с помощью диэлектрической проницаемости как функция частоты:

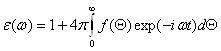. (7)

Лорентцом впервые была построена классическая, электронная теория, позволяющая получить явный вид (7). В рамках этой теории среду мы рассматриваем как совокупность электронных, гармонических, затухающих осцилляторов. Движение такого электронного осциллятора будет описываться следующим уравнением:

(8)

где  - масса электрона,  - заряд свободного электрона,  - коэффициент упругой связи электрона с ядром,  - коэффициент, обусловленный затуханием колебаний осциллятора,  - эффективное поле, действующее на электронный осциллятор. В общем случае  отличается от среднего макроскопического поля , входящего в уравнение Максвелла. Для разряженных газов . В такой среде под действием плоской линейно поляризованной вдоль Х электромагнитной волны (в такой волне вектор напряженности электрического поля  направлен вдоль X и не имеет своей ориентации при распространении, а фронт волны представляет плоскость) уравнение движения электрона (8) приобретает вид:

 (9)

где  - коэффициент затухания (экстенции),  - собственная частота электронного осциллятора,  - амплитуда электрического поля волны. Нетрудно показать, что решение уравнения (9) имеет вид:

. (10)

Учитывая связь диэлектрической проницаемости  с электронной поляризуемостью отдельного атома , можно записать:

,(11)

где  - количество атомов в единице объема. Используя (10), и считая, что магнитная проницаемость среды  (что приводит к следующей связи диэлектрической проницаемости и коэффициента преломления ), выражение (11) запишем в виде:

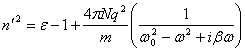. (12)

Выражение (12) показывает, что  является комплексной величиной, и поэтому может быть представлен в виде , где затухания среды.

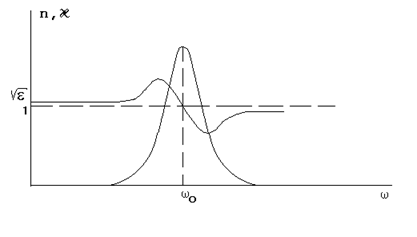Рис.1. Частотные зависимости  от  вблизи собственной частоты электронного осциллятора .

Для разряженных газов показатель преломления близок к единице, тогда в разложении в ряд Тейлора величин можно ограничиться двумя первыми членами. Учитывая условия равенства двух комплексных величин, можно записать следующие соотношение:

, (13)

 (14)

На рисунке 1 представлены частотная зависимость  от  вблизи собственной частоты электронного осциллятора .

В оптике принято понимать, что нормальной оптической дисперсией обладают те вещества, для которых , аномальной, - для которых . Исследуя графическую зависимость  (см. рис.1), можно сделать вывод, что область аномальной дисперсии (частоты между точками А и В) определяется процессом поглощения электронными осцилляторами электромагнитной волны вблизи частоты , а вдали от этой частоты наблюдается нормальная дисперсия. Таким образом, любое вещество обладает областями нормальной и аномальной дисперсии.