Понятие категорического силлогизма

Содержание

1. Что такое простой категорический силлогизм? Дайте его структуру

2. Для следующих терминов постройте диаграмму Эйлера: государства, республики, монархии

3. Постройте таблицу истинности следующей формулы

Список использованной литературы

1. Что такое простой категорический силлогизм? Дайте его структуру

Категорический силлогизм (или просто: силлогизм) – это дедуктивное умозаключение, в котором из двух категорических высказываний выводится новое категорическое высказывание.

Логическая теория такого рода умозаключений называется силлогистикой. Она была создана еще Аристотелем и долгое время служила образцом логической теории вообще.[1]

В силлогистике выражения "Все ... есть ...", "Некоторые ... есть ...", "Все ... не есть ..." и "Некоторые ... не есть..." рассматриваются как логические постоянные, т.е. берутся как единое целое. Это не высказывания, а определенные логические формы, из которых получаются высказывания путем подстановки вместо многоточий каких-то имен. Подставляемые имена называются терминами силлогизма.

Существенным является следующее традиционное ограничение: термины силлогизма не должны быть пустыми или отрицательными.

Примером силлогизма может быть:

Все жидкости упруги. Вода – жидкость. Вода упруга.

В каждом силлогизме должно быть три термина: меньший, больший и средний.

Меньшим термином называется субъект заключения (в примере таким термином является термин "вода").

Большим термином именуется предикат заключения ("упруга"). Термин, присутствующий в посылках, но отсутствующий в заключении, называется средним ("жидкость"). Меньший термин обозначается обычно буквой S, больший – буквой Р и средний – буквой М. Посылка, в которую входит больший термин, называется большей. Посылка с меньшим термином называется меньшей. Большая посылка записывается первой, меньшая – второй. Логическая форма приведенного силлогизма такова:

Все М есть Р. Все S есть М.

Все S есть Р.

В зависимости от положения среднего термина в посылках (является он субъектом или предикатом в большей и меньшей посылках) различаются четыре фигуры силлогизма. Схематически фигуры изображаются так:

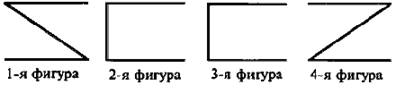
По схеме первой фигуры построен силлогизм:

Все птицы (М) имеют крылья (Р). Все страусы (S) – птицы (М).

Все страусы имеют крылья.

По схеме второй фигуры построен силлогизм:

Все рыбы (Р) дышат жабрами (М). Киты (S) не дышат жабрами (М).

Все киты не рыбы.

По схеме третьей фигуры построен силлогизм:

Все бамбуки (М) цветут один раз в жизни (Р). Все бамбуки (М) – многолетние растения (S).

Некоторые многолетние растения цветут один раз в жизни.

По схеме четвертой фигуры построен силлогизм:

Все рыбы (Р) плавают (М). Все плавающие (М) живут в воде (S).

Некоторые живущие в воде – рыбы.

Посылками и заключениями силлогизмов могут быть категорические суждения четырех видов: SaP, SiP, SeP и SoP.

Модусами силлогизма называются разновидности фигур, отличающиеся характером посылок и заключения.

Всего с точки зрения всевозможных сочетаний посылок и заключения в каждой фигуре насчитывается 64 модуса. В четырех фигурах 4 × 64 = 256 модусов.

Силлогизмы, как и все дедуктивные умозаключения, делятся на правильные и неправильные. Задача логической теории силлогизма – систематизировать правильные силлогизмы, указать их отличительные черты.

Из всех возможных модусов силлогизма только 24 модуса являются правильными, по шесть в каждой фигуре. Вот традиционно принятые названия правильных модусов первых двух фигур:

1-я фигура: Barbara, Celarent, Darii, Ferio, Barbari, Celaront; 2-я фигура: Cesare, Camestres, Festino, Baroco, Cesaro, Camestros.

В каждом из этих названий содержатся три гласных буквы. Они указывают, какие именно категорические высказывания используются в модусе в качестве его посылок и заключения. Так, название Celarent означает, что в этом модусе первой фигуры большей посылкой является общеотрицательное высказывание (SeP), меньшей – общеутвердительное (SaP) и заключением – общеотрицательное высказывание (SeP).

Из 24 правильных модусов силлогизма 5 являются ослабленными: заключениями в них являются частноутвердительные или частноотрицательные высказывания, хотя в случае других модусов эти же посылки дают общеутвердительные или общеотрицательные заключения (ср. модусы Cesare и Cesaro второй фигуры). Если отбросить ослабленные модусы, остается 19 правильных модусов силлогизма.[2]

Для оценки правильности силлогизма могут использоваться круги Эйлера, иллюстрирующие отношения между объемами имен.

Возьмем, для примера, силлогизм:

Все металлы (М) ковки (Р). Железо (S) – металл (М). Железо (S) ковко (Р).

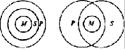
Отношения между тремя терминами этого силлогизма (модус Barbara) представляются тремя концентрическими кругами. Эта схема интерпретируется так: если все М (металлы) входят в объем Р (ковких тел), то с необходимостью S (железо) войдет в объем Р (ковких тел), что и утверждается в заключении "Железо ковко".

Другой пример силлогизма:

Все рыбы (Р) не имеют перьев (М). У всех птиц (S) есть перья (М). Ни одна птица (S) не является рыбой (Р).

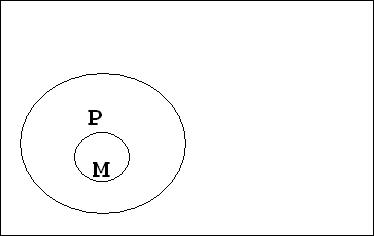
Отношения между терминами данного силлогизма (модус Cesare) представлены на рисунке. Он истолковывается так: если все S (птицы) входят в объем М (имеющие перья), а М не имеет ничего общего с Р (рыбы), то у S (птицы) нет ничего общего с Р (рыбы), что и утверждается в заключении.

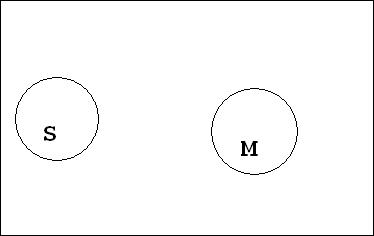
Пример неправильного силлогизма:

Все тигры (М) – млекопитающие (Р). Все тигры (М) – хищники (S). Все хищники (S) – млекопитающие (Р).

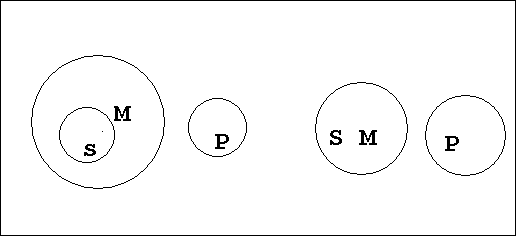
Отношения между терминами данного силлогизма могут быть представлены двояко, как это показано на рисунке. И в первом, и во втором случаях все М (тигры) входят в объем Р (млекопитающие) и все М входят также в объем S (хищники). Это соответствует информации, содержащейся в двух посылках силлогизма. Но отношение между объемами Р и S может быть двояким. Охватывая М, объем S может полностью входить в объем Р или объем S может лишь пересекаться с объемом Р. В первом случае можно было бы сделать общее заключение "Все хищники – млекопитающие", но во втором случае правомерно только частное заключение "Некоторые хищники – млекопитающие". Информации, позволяющей сделать выбор между этими двумя вариантами, в посылках не содержится. Значит, мы не вправе делать общее заключение. Силлогизм не является правильным.

В силлогизме, как и во всяком дедуктивном умозаключении, в заключении не может содержаться информация, отсутствующая в посылках. Заключение только развертывает информацию посылок, но не может привносить новую информацию, отсутствующую в них.[3]

В обычных рассуждениях нередки силлогизмы, в которых не выражается явно одна из посылок или заключение. Такие силлогизмы называются энтимемами. Примеры энтимем: "Щедрость заслуживает похвалы, как и всякая добродетель", "Он – ученый, поэтому любопытство ему не чуждо", "Керосин – жидкость, поэтому он передает давление во все стороны равномерно" и т.п. В первом случае опущена меньшая посылка "Щедрость – это добродетель", во втором – большая посылка "Всякому ученому не чуждо любопытство", в третьем – опять-таки большая посылка "Всякая жидкость передает давление во все стороны равномерно".

Для оценки правильности рассуждения в энтимеме следует восстановить ее в полный силлогизм.