Навигация
Методи моделювання й економіко-математичні методи
2.3 Методи моделювання й економіко-математичні методи
Моделювання передбачає конструювання моделі на основі попереднього вивчення об’єкта або процесу, виділення його суттєвих характеристик або ознак. Прогнозування економічних та соціальних процесів з використанням моделей включає розробку моделі, її експериментальний аналіз, співставлення результатів прогнозних розрахунків на основі моделі з фактичними даними стану об’єкта або процесу, коректування і уточнення моделі. В залежності від рівня управління економічними і соціальними процесами розрізняють макроекономічні, міжгалузеві, міжрайонні, галузеві, регіональні моделі та моделі мікрорівня (моделі розвитку фірми).
За аспектами розвитку економіки виділяють моделі прогнозування відтворення основних фондів, трудових ресурсів, цін та ін. Існує ряд інших ознак класифікації моделей: часовий, факторний, транспортний, виробничий. В сучасних умовах розвитку моделювання і практичному застосуванню моделей стала надаватися особлива значимість у зв’язку з посиленням ролі прогнозування і переходом до індикативного планування.
Розглянемо деякі із найбільш розроблених економіко-математичних моделей, які отримали широке застосування в практиці прогнозування економіки за кордоном (особливо в США).
Матричні моделі. До них належать моделі міжгалузевого балансу (МГБ): статичні та динамічні. Перші призначені для проведення прогнозних макроекономічних розрахунків на короткостроковий період (рік, квартал, місяць), другі – для розрахунків розвитку економіки країни на перспективу. Вони відображають процес відтворення в динаміці і забезпечують зв'язок прогнозу виробництва продукції (послуг) з інвестиціями.
Статична модель МГБ в системі народного господарства має вигляд:
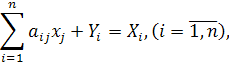
де ![]() коефіцієнти прямих витрат (середньогалузеві нормативи витрат продукції галузі і, яка використовується в якості засобів виробництва для випуску одиниці продукції галузі j);
коефіцієнти прямих витрат (середньогалузеві нормативи витрат продукції галузі і, яка використовується в якості засобів виробництва для випуску одиниці продукції галузі j); ![]() - обсяг виробництва продукції j-й галузі-споживача (j=
- обсяг виробництва продукції j-й галузі-споживача (j=![]() ;
; ![]() - валове виробництво продукції (послуг) і-й галузі-виробника (j=
- валове виробництво продукції (послуг) і-й галузі-виробника (j=![]() ;
; ![]() - об'єм кінцевого продукту і-й галузі-виробника.
- об'єм кінцевого продукту і-й галузі-виробника.
Рівняння ![]() характеризує міжгалузеві потоки і загалом проміжний продукт;
характеризує міжгалузеві потоки і загалом проміжний продукт; ![]() - кінцевий продукт;
- кінцевий продукт; ![]() - валовий суспільний продукт.
- валовий суспільний продукт.
Спрощена динамічна модель має вигляд
![]() =
=![]() +
+![]() +
+![]() , (j=
, (j=![]() ,
,
де t- індекс року; ![]() - продукція галузі і, яка направлена в якості виробничих інвестицій в t-му році для розширення виробництва в галузь j;
- продукція галузі і, яка направлена в якості виробничих інвестицій в t-му році для розширення виробництва в галузь j;![]() - об’єм кінцевого продукту і-ї галузі в t-му році за виключенням продукції, яка направлена на розширення виробництва. При переході до системи національних рахунків (СНР) моделі міжгалузевого балансу зазнають деяких змін. Рівняння
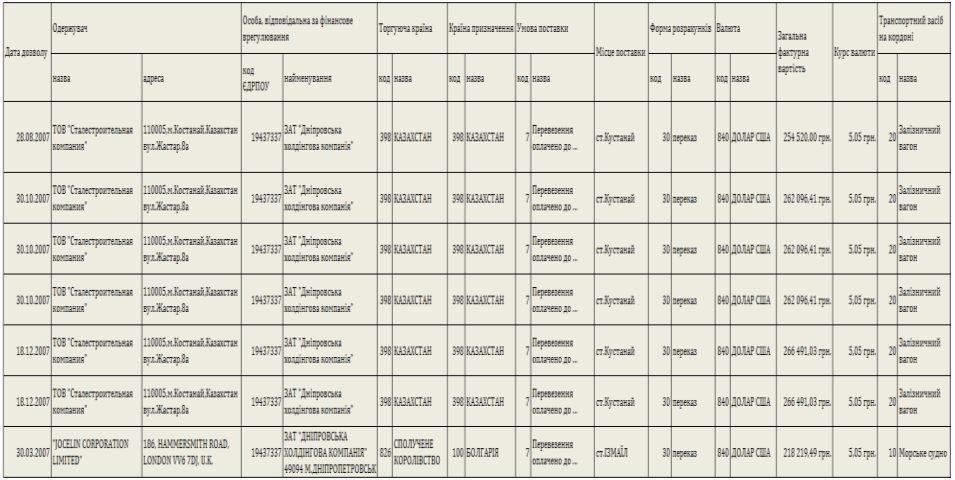
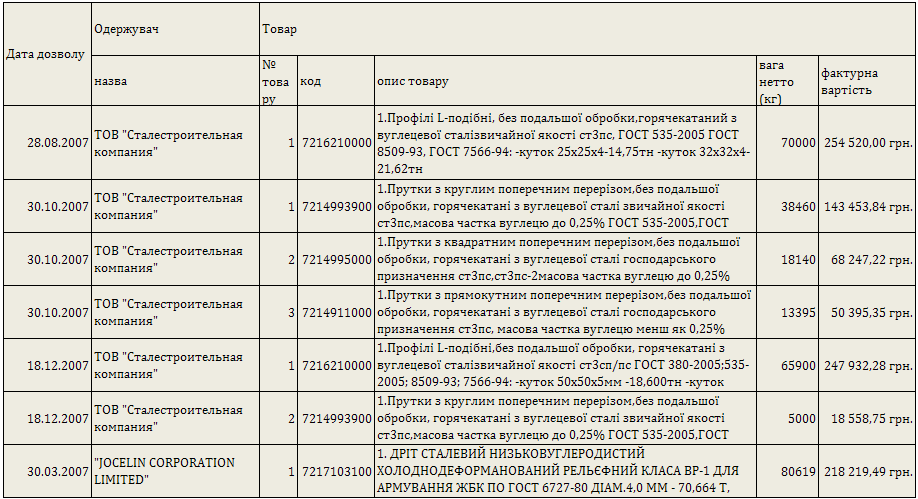
- об’єм кінцевого продукту і-ї галузі в t-му році за виключенням продукції, яка направлена на розширення виробництва. При переході до системи національних рахунків (СНР) моделі міжгалузевого балансу зазнають деяких змін. Рівняння ![]() характеризує проміжне споживання в сферах матеріального виробництва і нематеріальних послуг;
характеризує проміжне споживання в сферах матеріального виробництва і нематеріальних послуг; ![]() - кінцеве використання валового національного продукту (ВНП) в і-й галузі, яке включає кінцеве споживання (споживання домашніх господарств і державі витрати), валове накопичення і експорт.
- кінцеве використання валового національного продукту (ВНП) в і-й галузі, яке включає кінцеве споживання (споживання домашніх господарств і державі витрати), валове накопичення і експорт.
Моделі оптимального планування використовуються для визначення оптимального варіанту функціонування економіки в цілому і її окремих складових. Економіко-математична модель являє собою формалізований опис економічного процесу. Модель складається із цільової функції та системи обмежень. Цільова функція описує ціль оптимізації і являє собою залежність показника, за яким ведеться оптимізація, від незалежних змінних. Вплив кожної із змінних на величину цільової функції виражається коефіцієнтом – значенням показника, екстремум якого використовується в якості критерію оптимальності. Система обмежень відображає об’єктивні економічні зв’язки і залежності і являє собою систему рівностей і нерівностей. На макрорівні критерієм оптимальності є максимум валового національного продукту. На мікрорівні в якості критерію оптимальності можуть бути використані екстремуми показників: максимум прибутку, мінімум витрат, максимум випуску продукції (послуг) та ін.
Загальний вигляд моделі за розрахунком оптимального варіанта виробництва продукції:
Цільова функція
f(x)=![]() →ext, (i=
→ext, (i=![]()
Система обмежень
![]() ≤
≤![]() , (g=
, (g=![]() ,
,
![]() ≤
≤![]() , (k=
, (k=![]() ,
,
![]() ≤
≤![]() ≤
≤![]()
де ![]() - значення і-го показника на одиницю j-го виду продукції,
- значення і-го показника на одиницю j-го виду продукції, ![]() - норма розходу g-го виду сировини на виробництво одиниці j-го виду продукції;
- норма розходу g-го виду сировини на виробництво одиниці j-го виду продукції; ![]() - шукана кількість j-го виду продукції;
- шукана кількість j-го виду продукції; ![]() - наявний фонд g-го виду сировини;
- наявний фонд g-го виду сировини; ![]() затрати часу на k-м виді устаткування для виробництва одиниці j-го виду продукції;
затрати часу на k-м виді устаткування для виробництва одиниці j-го виду продукції; ![]() - дійсний фонд часу роботи k-го виду обладнання;
- дійсний фонд часу роботи k-го виду обладнання; ![]() ,
, ![]() - нижня та верхня межі випуску j-го виду продукції. Нижня межа встановлюється з урахуванням завдань на поставку продукції для державних потреб, верхня – з урахуванням попиту на продукцію. На макрорівні розрахунки проводяться в агрегованому вигляді. Система обмежень зазнає деяких змін. Замість обмеження по фонду часу роботи обладнання вводяться обмеження по фондовмісності або виробничій потужності (на галузевому рівні), розширений асортимент (конкретні види продукції) замінюється на груповий.
- нижня та верхня межі випуску j-го виду продукції. Нижня межа встановлюється з урахуванням завдань на поставку продукції для державних потреб, верхня – з урахуванням попиту на продукцію. На макрорівні розрахунки проводяться в агрегованому вигляді. Система обмежень зазнає деяких змін. Замість обмеження по фонду часу роботи обладнання вводяться обмеження по фондовмісності або виробничій потужності (на галузевому рівні), розширений асортимент (конкретні види продукції) замінюється на груповий.
Слід зазначити, що, не зважаючи на багатоманітність розроблених моделей і наявність пакетів програм для проведення багатоваріантних розрахунків, оптимізаційні задачі носять, як правило, експериментальний характер.
Економіко-статистичні моделі. Вони використовуються для встановлення кількісної характеристики зв’язку, залежності і взаємообумовленості економічних показників. Система такого роду моделей включає: однофакторні, багатофакторні і економетричні моделі. Приклади однофакторних моделей:
y=a+bx; y=a+b/x; y=a+b lg x та ін.,
де у – значення прогнозованого показника; а-вільний член, який визначає положення початкової точки лінії регресії в системі координат; x- значення фактора; параметр b характеризує норму зміни у на одиницю x.
Багатофакторні моделі дозволяють одночасно враховувати вплив декількох факторів на рівень прогнозованого показника. При цьому останній виступає як функція від факторів:
у=f (х1,х2,х3…, хn),
де х1,х2,х3…, хn – фактори.
При лінійній залежності багатофакторні моделі можуть бути представлені наступним рівнянням:
у=а0+а1х1+а2х2+…+аnхn,
де а0 – вільний член; а1, а2,…аn – коефіцієнти регресії, які показують ступінь впливу відповідного фактора на прогнозований показник при фіксованому значенні інших факторів.
При нелінійній залежності багатофакторна модель може мати вигляд
y=a·![]() ·
·![]() ·…·
·…·![]() .
.
Багатофакторні моделі використовуються при прогнозуванні макроекономічних показників, попиті на продукцію, собівартості, цін, прибутку та інших показників.
Економетричною моделлю називають систему регресійних рівнянь, які описують взаємозв’язки і залежності основних показників розвитку економіки. Вони дозволяють прогнозувати широке коло показників (ВНП, доходи населення, споживання товарів і послуг, та ін.).
Імітаційні моделі. Мета імітаційного моделювання полягає в відтворенні поведінки системи на основі результатів аналізу більш суттєвих взаємозв’язків між її елементами. Імітаційні моделі дозволяють відтворити реальні процеси і передбачити результати різноманітних дій.
Моделі прийняття рішень засновані на теорії ігор. Вони застосовуються в умовах невизначеності або ситуаціях, коли інтереси сторін не співпадають. Кожна із сторін приймає таке рішення, тобто вибирає таку стратегію дій, яка з їх точки зору забезпечує найбільший виграш або найменший програш. Причому кожній із сторін зрозуміло, що результат залежить не тільки від своїх дій, але й від дій партнерів. Наприклад, протиборство конкурентів в процесі боротьби за ринок збуту конкретного виду продукції.
Моделі мережевого планування застосовуються з метою скорочення термінів виконання складних проектів та інших робіт і оптимального використання призначених для цього ресурсів. Термін «мережеве планування» набуває в останній час все більшої популярності. Основою мережевого планування служить зображення комплексу взаємопов’язаних робіт у виді графа, зазвичай названого мережевим графіком, діаграмою, логічною мережею або мережевою моделлю. В мережевому графіку відображається послідовність етапів, необхідних для досягнення раніше поставленої мети.
Метод міжгалузевого балансу базується на принципах розробки міжгалузевого балансу, які були обґрунтовані спеціалістами бувшого СССР і розвинуті за кордоном. (В. Леонтьєвим в США). Використання методу на основі моделі міжгалузевого балансу дозволяє виконувати прогнозування розвитку економіки і її галузевої структури, виходячи із кінцевих потреб (кінцевого використання ВНП).
В математичній формі міжгалузевий баланс являє собою систему рівнянь:
![]() +
+![]() …+
…+![]() +
+![]() =
=![]() ,
,
![]() +
+![]() +…+
+…+![]() +
+![]() =
=![]() ,
,
…………………………………
![]() +
+![]() +…+
+…+![]() +
+![]() =
=![]() .
.
Для рішення системи рівнянь складається матриця коефіцієнтів прямих витрат. Шляхом математичних перетворень формується матриця коефіцієнтів повних витрат. Потім на основі представленої вище системи рівнянь проводиться розрахунок міжгалузевих поставок, в цілому проміжного продукту і формується таблиця міжгалузевого балансу.
До методів оптимізації належать лінійне програмування і цілочисельне програмування. За допомогою методів оптимізації створюється можливість вибору оптимального варіанту використання ресурсів і задоволення потреб в продукції, розміщення виробничих сил, раціонального прикріплення поставщиків до споживачів і вирішувати інші задачі. Оптимізаційні розрахунки здійснюються на основі розроблених економіко-математичних моделей і вихідної інформації з використанням спеціальних пакетів програм. Результати оптимізаційних розрахунків носять рекомендаційний характер.
Сутність кореляційно-регресивного методу полягає в визначенні залежності показника від різних факторів. Цей метод передбачає встановлення наявності кореляційного зв’язку між прогнозованим показником і факторами, які на нього впливають. Форма зв’язку характеризує зміну значень однієї ознаки від зміни іншої. Вона може бути лінійною і нелінійною, відповідно виражається рівняннями. Одночасно з встановленням форми зв’язку визначається тіснота зв’язку, яку характеризує коефіцієнт кореляції (R).
Похожие работы
... Ринок цінних паперів України.- 2003.- №3-4.- С. 55-57 49. Осовська Г. В. Основи менеджменту / Навчальний посібник / Київ: „Кондор", 2003. - с. 89-91 - 553 с. 50. Панасенко О.В. Вдосконалення фінансового планування на підприємстві з використанням економіко-математичних моделей// Актуальні проблеми економіки.- 2008.- №7.- С. 219-227 51. Петленко Ю.В. Фінансовий менеджмент: навчальний посібник.- ...
... ї економіки значно підвищується матеріальна відповідальність керівника підприємства за його фінансовий стан. Саме тому зросла важливість перспективного, поточного та оперативного фінансового планування для забезпечення фінансового стану та підвищення рентабельності підприємств. Фінансове планування є необхідним для фінансового забезпечення розширення кругообороту виробничих фондів, досягнення ...
... полягає в тому, що воно дає можливість визначити життєздатність проекту підприємства за умов конкуренції і є інструментом одержання фінансової підтримки від зовнішніх інвесторів. Отже, основними завданнями фінансового планування на підприємстві є: · забезпечення виробничої та інвестиційної діяльності необхідними фінансовими ресурсами; · установлення раціональних фінансових відносин із суб’є ...
... і, фінансові прогнози, прогноз попиту на його продукцію чи послуги і чому підприємець вважає, що його справа матиме успіх. РОЗДІЛ 3 ШЛЯХИ ВДОСКОНАЛЕННЯ БІЗНЕС ПЛАНУВАННЯ НА ПІДПРИЄМСТВІ 3.1 Пропозиції щодо вдосконалення бізнес планування на підприємстві У центрі уваги комерційної організації завжди знаходиться покупець з його інтересами і побажаннями. Від того, як складаються відносини з ...
0 комментариев