Интерференция тождественных частиц.
Как отмечалось, все электроны эквиволентны друг другу. Это означает, что в случае системы с несколькими электронами в различных состояниях принципиально невозможно указать, какой из электронов реально находится в каждом из состояний. Общие принципы квантовомеханического описания позволяют описать эту “классически странную” ситуацию весьма просто: существует множество ортогональных базисных состояний системы (на самом деле неразличимых), соответствующих всевозможным размещениям “мысленно занумерованных” электронов по одноэлектронным состояниям, а реализующееся в природе состояние есть их суперпозиция. Например, простой двухэлектронной системой с двумя состояниями является атом гелия, один электрон которого находится на самом нижнем энергетическом уровне 
, а другой - на ближайшем возбужденном уровне 
. Мыслимы симметричная и антисимметричная линейные комбинации эквиволентных состояний:
(1) 
.
В рамках релятивистской квантовой теории исходя из требований релятивистской инвариантности и положительности числа частиц в системе может быть получен однозначный ответ на вопрос, какое из этих двух состояний реализуется в природе: амплитуды тождественных частиц с полуцелым спином интерферируют, всегда образуя антисиметричные состояния, в случае систем тождественных частиц с целым спином всегда реализуются симметричные системы . По мнению Р.Фейнмана сложность доказательства столь просто формулируемого правила свидетельствует о неполноте наших знаний фундаментальных законов природы.
Фермионы.
Из правила интерференции непосредственно следует принцип Паули для электронов: в случае нахождения двух электронов в полностью эквивалентных состояниях (все квантовые числа одинаковы) разность в (1) превращается в 0, что означает равную нулю вероятность реализации такого состояния, т.е. его невозможность.
Специфическое свойство частиц с полуцелым спином (“фермионов”) не занимать состояния с уже имеющейся частицей видоизменяет функцию их распределения по сравнению с классической статистикой Больцмана:
(2) 
.
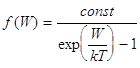Распределение (2) получило название статистики Ферми-Дирака.
Указанному свойству фермионов наш мир “обязан” своим многообразием: если бы запрета Паули не существовало, элетроны всех атомов собирались бы на самом нижнем энергетическом уровне, химические свойства различных элементов были бы одинаковыми.
Список литературы
Для подготовки данной работы были использованы материалы с сайта http://study.online.ks.ua/
Похожие работы
оявилась немного раньше и по другим причинам (как она появилась, мы это в своё время обсудим). h – это некоторая константа с размерностью , такая величина в физике называется действием. Импульс фотона – это энергия, делённая на скорость света: . Здесь полезно вспомнить релятивистскую формулу для связи между энергией и скоростью или, что тоже, с импульсом: . Когда импульс равен нулю (p = 0), , это ...
... -нибудь значимых масс, зарядов, электромагнитных и прочих полей. Поместим в него тела отсчета и пробное, не способные ощутимо исказить геометрию пространства. Для свободной системы тел проекции их мировых линий в любом евклидовом сечении физического пространства будут, в общем случае, прямыми линиями. Поэтому интерес представляют гиперболические сечения (плоскости Минковского), см. рис.1. Рис. ...
... сделавшие важнейшие открытия в области физики, пытались вместе с тем интерпретировать эти открытия с той или иной философской точки зрения. Благодаря таким взглядам был открыт эффект Бозе-Эйнштейновской конденсации. К 1920 физики были уже довольно хорошо знакомы с двойственной природой света: результаты одних экспериментов со светом можно было объяснить, предполагая, что свет представляет собой ...
... , они вновь указывают на составной характер этих частиц и на новую, более глубокую симметрию. 4. Скрытая симметрия и объединение электромагнитных и слабых взаимодействий Крупным достижением, полученным на основе принципа локальной калибровочной инвариантности, стало развитие американскими физиками Стивеном Вайнбергом, Шелдоном Глэшоу и пакистанским ученым Абдусом Саламом теории, объединяющей ...
0 комментариев