Чтобы изменить состав генофонда, требуется нечто большее, чем генетическая рекомбинация.
В научном мире нечасто случается, чтобы разные ученые независимо друг от друга наткнулись на одну и ту же закономерность, но все же таких примеров достаточно, чтобы заставить нас поверить в существование «духа времени». К их числу относится и закон Харди—Вайнберга (известный также как закон генетического равновесия) — одна из основ популяционной генетики. Закон описывает распределение генов в популяции. Представьте себе ген, имеющий два варианта — или, пользуясь научной терминологией, два аллеля. Например, это могут быть гены «низкорослости» и «высокорослости», как в случае менделевского гороха (см. Законы Менделя), или наличие/отсутствие предрасположенности к рождению двойни. Харди и Вайнберг показали, что при свободном скрещивании, отсутствии миграции особей и отсутствии мутаций относительная частота индивидуумов с каждым из этих аллелей будет оставаться в популяции постоянной из поколения в поколение. Другими словами, в популяции не будет дрейфа генов.
Рассмотрим этот закон на простом примере. Назовем два аллеля Х и х. Тогда у особей могут встречаться четыре следующие комбинации этих аллелей: ХХ, хх, хХ и Хх. Если обозначить через p и q частоту встречаемости индивидуумов с аллелями Х и х соответственно, то согласно закону Харди—Вайнберга
p2 + 2pq + q2 = 100%,
где p2 — частота встречаемости индивидуумов с аллелями ХХ, 2pq — с аллелями Хх или хХ, а q2 — частота встречаемости индивидуумов с аллелями хх. Эти частоты, при соблюдении сформулированных выше условий, будут оставаться постоянными из поколения в поколение, независимо от изменения количества индивидуумов и от того, насколько велики (или малы) p и q. Этот закон представляет собой модель, используя которую генетики могут количественно определять изменения в распределении генов в популяции, вызванные, например, мутациями или миграцией. Другими словами, этот закон является теоретическим критерием для измерения изменений в распределении генов.
Комментировать Годфри Харолд ХАРДИ
Godfrey Harold Hardy, 1877–1947
Английский математик, родился в Кранли, графство Суррей. Сын учителя рисования. Изучал математику в Кембриджском и Оксфордском университете. Пожалуй, самую большую известность Харди принесли совместные работы с Джоном Идензором Литлвудом (John Edensor Littlewood, 1885–1977) и позднее с индийским математиком-самоучкой Cриниваса Рамануджаном (Srinivasa Aaiyangar Ramanujan, 1887–1920), который работал клерком в Мадрасе. В 1913 году Рамануджан послал Харди список доказанных им теорем. Признав гениальность юного клерка, Харди пригласил его в Оксфорд, и в течение нескольких лет, предшествовавших безвременной смерти Рамануджана, они опубликовали серию блестящих совместных работ.
***
Вильгельм ВАЙНБЕРГ
Wilhelm Weinberg, 1862–1937
Немецкий врач, имевший большую частную практику в Штуттгарте. По воспоминаниям современников, помог появиться на свет 3500 младенцам, в том числе по крайней мере 120 парам близнецов. На основании собственных наблюдений над рождением близнецов и переоткрытых генетических законов Менделя пришел к выводу, что предрасположенность к рождению двуяйцевых (неидентичных) близнецов передается по наследству.
Список литературы
Для подготовки данной работы были использованы материалы с сайта http://elementy.ru/
Похожие работы
... локализовать на хромосомах главные гены, управляющие поведением, и еще многое другое. Цель данной контрольной работы – изучение одного из вопросов психогенетики: «В чем заключается закон Харди-Вайнберга и каковы его основные ограничения?», что нашло свое выражение в трех главах данной работы. 1 Знание необходимых основ психогенетики 1.1 Введение в популяционную генетику Эволюция, идущая ...
... поколений. Естественно, особенно они заметны, если популяция находится в изоляции, т.е. отсутствует миграция генов извне. Известны сообщества такого рода в человеческом обществе. Часть 2 Математические модели нейронных систем Изучение нейронных систем -одно из самых романтических направлений научных исследований, поскольку нейронные системы присущи как человеку, так и животным. Самая ...
... показывают: Таким образом, . Совершенно аналогично: , , . В равновесных состояниях частоты гамет являются произведениями частот соответствующих генов. Верно и обратное утверждение. Часть 2 Математические модели нейронных систем Изучение нейронных систем -одно из самых романтических направлений научных исследований, поскольку нейронные системы присущи как человеку, так и животным. Самая ...
... аллеля равна 0.99, а частота рецессивного аллеля альбинизма – 0.01. Общая частота аллелей в популяции составляет 100%, или 1.0, поэтому Частота доминантного аллеля + Частота рецессивного аллеля =1 0.99 + 0.01 =1 Как это принято в классической генетике, аллели можно обозначить буквами, например, доминантный аллель (нормальная ...


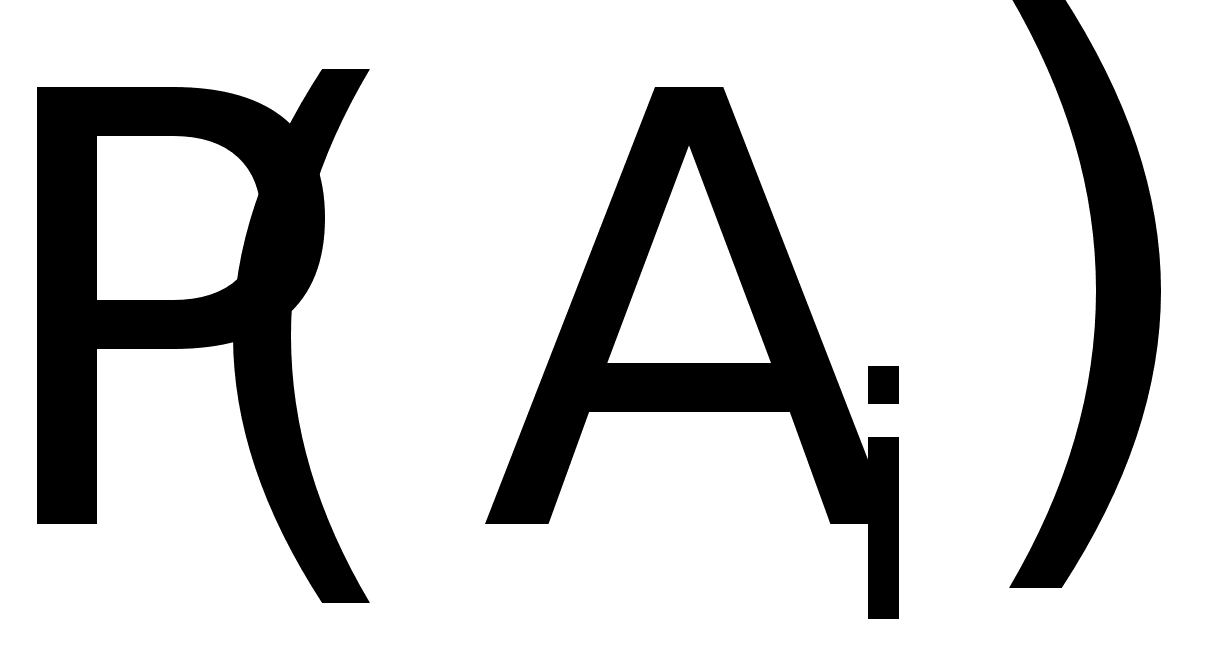
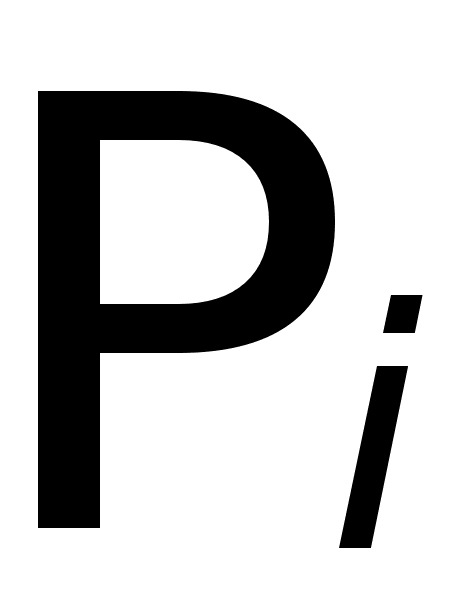
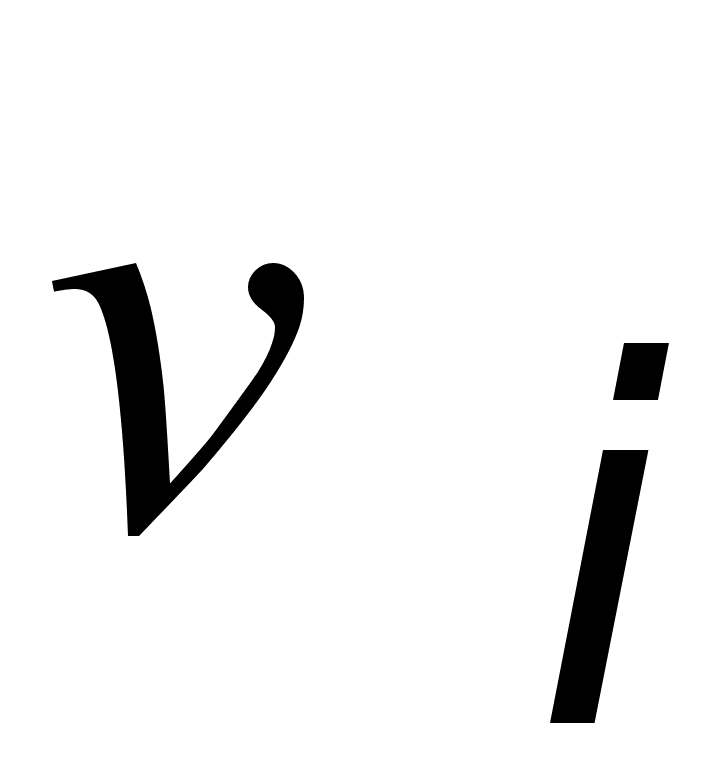
0 комментариев