Навигация
Рассеяние гамма – квантов. [1,4,5]
1.2. Рассеяние гамма – квантов. [1,4,5]
Строго говоря, в широком спектре излучения наблюдается два вида рассеяния: рассеяние на свободных электронах (некогерентное) и на связанных электронах (когерентное).
1.2.1. Некогерентное (Комптоновское рассеяние).
Забегая в перёд, замечу, что термин свободные имеет смысл в том, что энергия гамма – кванта намного превышает энергию связи. Орбитальные электроны в данном случае можно считать покоящимся или свободным. В акте взаимодействия квант передаёт электрону часть своей энергии и вылетает с изменением своей первоначальной траектории. Количественно это можно описать:
Ey* = Ey / (1+ [ Ey / (mec2)]*(1-cos θ)) [1.3]
Векторно этот процесса можно проиллюстрировать рис 3 – а [1].
Рис 3.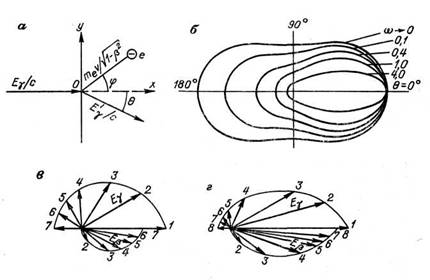
Как видно из рисунка, гамма – квант после взаимодействия отклоняется на некоторый угол φ, численно описываемый:
tg φ = [1 / (1 + ω)] ctg (θ / 2) [1.4]
С разной долей вероятности, углы рассеяния лежат в 4π – области. Вероятность рассеяния на определённый угол зависит от энергии гамма –кванта до взаимодействия. С ростом энергии вероятность обратного рассеяния уменьшается. Зависимость сечения рассеяния от энергии ( Ey / me c2) в графическом виде приведена на рис 1.2
Дифференциальное сечение Комптон – эффекта на электроне dσe / dΩ, отнесённое к единице телесного угла, описывается формулой Клейна – Нишины – Тамма:
dσкмикр / dΩ = [re2 / 2] *[(1+cos2θ) / (1+ω(1-cos θ))2] * {1+[ω2(1- cosθ)2 / [(1 +cos2θ)(1+ω(1 – cosθ))]} [1.5]
Дифференциальное сечение Комптон – эффекта имеет смысл вероятности рассеяния кванта под данным углом θ в единичный телесный угол dΩ. При интегрировании выражения 1.5 по углу 4π получим полное сечение комптоновского взаимодействия (имеет смысл микроскопического): σкмикр = 2πre2 {((1+ω) /ω2)[(2(1+ω)/(1+2ω)) – (ln(1+2ω)/ω] + (ln(1+2ω)/2ω) – ((1+3ω)/(1+2ω)2)} [1.6]
Из формулы 1.3 видно, что при рассеянии под малыми углами потери энергии минимальны. С увеличением угла θ энергия рассеяния уменьшается и принимает минимальное значение при рассеянии назад. Полное сечение комптоновского взаимодействия с изменением энергии падающего кванта меняется незначительно, плавно уменьшаясь с увеличением энергии. В энергетическом окне 0,01 – 3 МэВ плавно падает от ≈ 0,6 до ≈ 0,12 Барн.
С уменьшением энергии падающих гамма – квантов разница между Ey и Ey* уменьшается при рассеянии под любым углом, к тому же Ey* не принимает нулевых значений.
С другой стороны в процессе комптоновского взаимодействия гамма – квант передаёт электрону часть своей энергии, но не исчезает. Сечение этого процесса характеризует сечение истинного комптоновского поглощения. Сумма сечения истинного комптоновского поглощения σкмикр п и сечение собственно комптоновского рассеяния σкмикр р есть полное микроскопическое сечение комптоновского рассеяния.
Микроскопическое сечение предпологает наличие в рассматриваемом объёме как – бы одного атома, на электронах которого рассеивается гамма – квант. Для перехода к макроскопичекому сечению надо учесть электронную плотность среды. σкмакр характеризует убыль гамма – квантов из узкого единичного пучка при прохождении через среду (экран). Действительно, гамма – квант взаимодействуя с электроном поменяет свою траекторию и, тем самым, удалится из пучка, причем эти удаления будут тем чаще, чем больше рассеяний на единицу длинны пучка, что соответствует плотности вещества.
σкмакрос = σкмикр * ρ Аав * [Z / A] [1.7]
1.2.2 Рассеяние на связанных электронах (Рэлеевское).
Данный вид рассеяния наблюдается при энергиях гамма – квантов менее 20 – 50 кэВ. Сечение взаимодействия прямо зависит от Zэф среды. Преобладает над некогерентным в полосе энергий меньше 20 кэВ. Не регистрируется при ГГКп.
1.3. Образование электронно – позитронных пар.
Процесс имеет энергетический порог примерно 1,022 МэВ. Суть процесса в том, что в поле ядра квант может превратиться в электронно – позитронную пару. Процесс сопровождается отдачей кванта, вызванное рекомбинацией позитрона с одним из свободных электронов. Является помехой для обоих модификаций. Как физическая основа нигде пока не используется.
Глава 2. Плотностная модификация Гамма – Гамма каротажа.
В варианте ГГКпл породы облучают потоком жёстких гамма – квантов с энергиями 0,5 – 5МэВ, мягкая компонента поглощаются с помощью фильтра.
Похожие работы
... , в основном, хорошего качества. Расхождение в показаниях не превышает 5%. Кавернограммы преимущественно хорошего качества, погрешность измерения диаметров скважин не превышает 1,5 см [10]. 6. ОБРАБОТКА И ИНТЕРПРЕТАЦИЯ ДАННЫХ ГЕОФИЗИЧЕСКИХ ИССЛЕДОВАНИЙ СКВАЖИН Основными задачами при изучении геологического разреза нефтяных и газовых скважин является: 1) расчленение разрезов на пласты ...
0 комментариев