Навигация
Основное уравнение безнапорного равномерного движения
3. Основное уравнение безнапорного равномерного движения
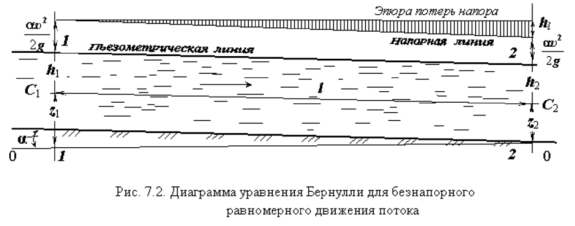
Уравнение Бернулли для двух проведенных вертикально сечений (1-1 и 2-2) открытого потока при равномерном движении (рис. 7.2) будет выглядеть следующим образом:
![]()
(значения параметров записаны для центров живых сечений потока)
α1 = α2 = α;
h1 = h2 = h;
![]()
![]()
![]()
![]()
![]()
где ![]() – геометрический уклон.
– геометрический уклон.
Для определения средней скорости безнапорного равномерного потока получена формула Шези, в которой в качестве расчетного берется геометрический уклон:
![]()
где ![]() – коэффициент Шези, рассчитываемый по формулам Маннинга
– коэффициент Шези, рассчитываемый по формулам Маннинга
![]() – Н. Н. Павловского и многим другим (Гангилье-Куттера, И. И. Агроскина и пр.).
– Н. Н. Павловского и многим другим (Гангилье-Куттера, И. И. Агроскина и пр.).
В этих формулах:
n – коэффициент шероховатости, определяемый по справочным данным
y – переменный показатель степени: ![]()
Расход в сечении русла определяется по формуле
![]()
![]() (*)
(*)
где K – модуль расхода или расходная характеристика ![]()
4. Гидравлически наивыгоднейшее сечение канала
Из формулы (*) следует, что при равных условиях α = const, i = const расход в сечении будет возрастать при увеличении гидравлического радиуса, т. е. канал будет пропускать тем больший расход, чем будет меньше смоченный периметр χ. Кроме того, при χmin снижаются и возможные потери на фильтрацию через борта и дно канала.
Гидравлически наивыгоднейшим сечением канала является сечение, способное при заданной площади обеспечить максимальную пропускную способность.
Как известно из геометрии, наименьшим периметром (из всех возможных) обладает круг, и гидравлически наивыгоднейшим сечением для открытых каналов было бы сечение, имеющее форму полукруга. Далее при данной площади меньшими периметрами обладают правильные многоугольники, причем длина их периметра будет тем меньше, чем больше число сторон.
Следовательно, далее по выгодности идут различные сечения в форме половин правильных многоугольников, например половина шестиугольника, т. е. равнобочная трапеция с углом наклона боковых сторон α = 60°. Из прямоугольных профилей наивыгоднейшим является сечение в виде половины квадрата. Величина гидравлического радиуса для всех этих сечений равняется половине наибольшей глубины наполнения.
Гидравлически наивыгоднейшее сечение часто не является экономически наивыгоднейшим. Например, полукруглое отверстие гидравлически выгоднее прямоугольного, но благодаря большей своей стоимости оно не используется при строительстве каналов.
На практике наиболее употребительны каналы трапецеидального сечения (рис. 7.1, в) со следующими элементами гидравлической характеристики:
![]()
![]()
![]()
где m = ctg α – коэффициент откоса русла.
Полукруглые или многогранные сечения применяются значительно реже, ввиду трудности их выполнения и значительной стоимости. Однако в наиболее часто встречающихся случаях земляных стенок трапецеидальные сечения редко получают форму наивыгоднейшего профиля в виде половины правильного шестиугольника с углом α = 60°, так как при этом требуется крепление боковых стенок канала. Обычно этот угол выбирается в соответствии с углом естественного откоса грунта, и задача сводится к определению при заданных площади сечения и угле откоса соотношения между шириной и глубиной, при котором смоченный периметр будет наименьшим.
Из формулы площади ![]() , следует
, следует ![]()
При подстановке значения b в формулу и взятии производной, значение которой при минимальном α будет равно нулю, для соотношения b/h будет получено
![]()
Для трапецеидального гидравлически наивыгоднейшего профиля значения относительной ширины по дну приведены в таблице.
| m | 0 | 0,25 | 0,5 | 0,75 | 1 | 1,5 | 2 | 2,5 | 3 | 4 |
| b/h | 2 | 1,56 | 1,236 | 1 | 0,828 | 0,606 | 0,,472 | 0,385 | 0,325 | 0,246 |
Таким образом, каналы гидравлически наивыгоднейшего профиля представлены относительно узкими и глубокими.
В связи с этим крупные каналы не проектируют с гидравлически наивыгоднейшим профилем. Малые каналы, особенно мелиоративные, целесообразно проектировать с гидравлически наивыгоднейшим профилем (сечением) или с профилем, близким к гидравлически наивыгоднейшему.
5. Расчетные скорости воды в канале
При проектировании каналов допускаемые скорости течения, так же как и при проектировании напорных трубопроводов, имеют большое экономическое значение, так как выбор скорости течения определяет размеры канала.
Крайние значения скоростей (минимальные и максимальные) ограничиваются двумя причинами. При малых скоростях сечение канала получается большим, что, увеличивая объем земляных работ, удорожает строительство. Кроме того, при малых скоростях происходит заиление канала вследствие оседания взвешенных в жидкости частиц. При больших скоростях сечение получается меньше. Это уменьшает объем земляных работ, однако при этом требуется более прочное покрытие стенок канала, что требует дополнительных затрат. Правильный выбор расчетной скорости, поэтому имеет большое значение. В каждом отдельном случае этот вопрос должен решаться конкретно с учетом всех местных условий.
Расчетные скорости не должны быть больше допускаемых. В качестве допускаемых принимаются скорости, неразмывающие грунт или одежды (укрепления откосов и дна) каналов. Значения их зависит от глубины и материала, из которого сложены стенки каналов.
Для определения неразмывающей скорости может быть рекомендована формула Б. И. Студеничникова, полученная по данным лабораторных и натурных исследований в широком диапазоне крупностей частиц несвязного грунта
![]()
где h – глубина.
d – средневзвешенный диаметр частиц грунта (берутся в метрах)
В то же время скорости не должны быть ниже критических значений скоростей, при которых начинается выпадение наносов и происходит заиление каналов, ведущее к их зарастанию. Эти скорости называются незаиляющими.
Незаиляющие скорости в каналах могут быть ориентировочно определены по формуле Гиршкана
![]()
где k – коэффициент, изменяющийся от 0,33 до 0,55 в зависимости oт гидравлической крупности частиц (1,5–3,5 мм/c).
Гидравлическая крупность – это скорость равномерного падения частицы в неподвижной воде.
Для предотвращения зарастания канала достаточно поддержать в нем среднюю скорость течения воды не ниже 0,5 м/с. В обычных водопроводящих каналах расчетные скорости находятся в пределах 0,5 – 3 м/с в зависимости от типа грунтов или одежды канала.
В условиях зимнего режима большой опасностью на каналах может стать глубинный лед - шуга. Основная причина появления в канале шуги - переохлаждение воды. После образования ледяного покрова дальнейшее понижение температуры воздуха вызывает лишь увеличение толщины льда, но не выделение шуги. Для быстрого образования поверхностного льда необходимо скорости течения воды в каналах на этот период уменьшить до 0,5м/с. Во избежание размыва льда нормальные скорости под ним не должны превышать 1,2-1,5 м/с. При скоростях, больших 2,25 м/с, поверхностный лед в каналах не образуется.
Выбор допустимых скоростей имеет большое экономическое значение при проектировании и эксплуатации искусственных водотоков.
Использованная литература
1. Г. В. Железняков. Гидравлика и гидрология. М.: “Транспорт”, 1989.
2. Справочник по гидравлике. Под редакцией В.А. Большакова. Киев: «Вища школа», 1977.
3. Т.М. Башта. Машиностроительная гидравлика. Справочное пособие. М.: «Машгиз»,1963.
4. Т.М. Башта. Гидравлика, гидравлические машины и гидравлические приводы. М.: «Машиностроение», 1970.
5. Р.Р. Чугаев. Гидравлика. Изд.3., М.- Л.: «Энергия», 1975 г.
6. Д.В. Штеренлихт. Гидравлика. М.: «Энергоатомиздат», 1984 г.
Похожие работы
... фундамента. 59 Нормативный срок службы водозаборной арматуры, годы: А) 5; В) 10; С) 15; D) 20; E) 25. 60 Нормативный срок службы чугунных радиаторов, годы: А) 5; В) 10; С) 20; D) 30; E) 40. 61 Какой параметр ограничивается во всех инженерных системах? A) давление; B) скорость; C) температура; D) вязкость; E) расход. 62 Какая инженерная система рассчитывается для трех различных ...
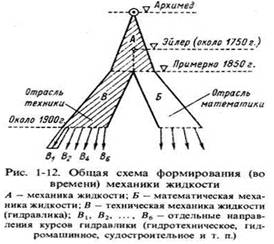
... два различных направления: "математическую механику жидкости" (см. область Б) и "техническую механику жидкости" (см. область В). Как отмечают (например, Г. Рауз и С. Инце в своей известной книге "История гидравлики"),' математическая механика жидкости зародилась еще в трудах Л. Эйлера (в середине XVIII в.). Что касается технической механики жидкости (гидравлики), то это направление механики, как ...
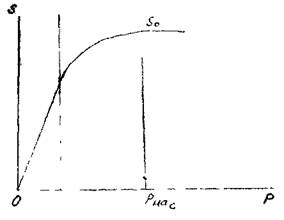
... эффект к турбулентности называется кавитация. При кавитации в толще жидкости появляются пустоты. Это поток, который ещё “ламинарнее” ламинарного потока! Существуют три режима движения жидкости: турбулентный, ламинарный и кавитация. Качественное различие между режимами заключается в отношении скорости движения молекул жидкости к скорости движения всего объёма жидкости. При равенстве этих скоростей ...
... . Для оценки режима течения жидкости вводят специальный критерий; число кавитации К f ' 7. Истечение жидкости из отверстий и насадков > 7.1. Отверстие в тонкой стенке Одной из типичных задач гидравлики, которую можно назвать задачей прикладного характера, является изучение процессов, связанных с истечением жидкости из отверстия в тонкой стенке и через насадки. ...
0 комментариев