Навигация
Предварительные вычисления. Вычисление рабочих координат пунктов
1.2 Предварительные вычисления. Вычисление рабочих координат пунктов
Цель предварительных вычислений в полигонометрии – определение качества полевых измерений и соответствия их по точности требованиям инструкции, а также подготовка результатов измерений для уравнительных вычислений.
В результате предварительных вычислений определяют невязки ходов и полигонов и сравнивают их с предельными значениями, установленными для данного класса или разряда соответствующими инструкциями.
Угловую невязку fβ находят для разомкнутого хода по формуле
![]()
Далее распределяем полученную угловую невязку поровну на каждый угол вычисляя поправки по формуле:
![]() .
.
По исправленным за угловую невязку углам вычисляют дирекционные углы
![]()
Далее вычисляют приращения координат и определяют невязки в приращениях по формулам:
![]()
![]()
По невязкам ![]() и
и ![]() находят абсолютную и относительную линейные невязки хода или полигона
находят абсолютную и относительную линейные невязки хода или полигона
![]()
Невязки ![]() и
и ![]() распределяют прямо пропорционально длинам линий хода
распределяют прямо пропорционально длинам линий хода
![]() и
и ![]()
По исправленным за поправки приращениям координат вычисляют координаты пунктов хода.
1.3 Уравнивание угловых и линейных величин
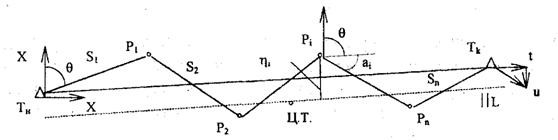
За узловую обычно принимают линию того звена, в котором наибольшее число их, В данном случае за узловое принято направление на вспомогательную точку, не входящую в сеть 6-6а. По каждому звену, начиная от твёрдой линии, вычисляют дирекционные углы узловой линии
![]()
где ![]() - исходный дирекционный угол
- исходный дирекционный угол
![]() - сумма левых по ходу углов
- сумма левых по ходу углов
(n+1) – число углов в звеньях
Значения вычисленных дирекционных углов записывают в таблицу 3. Вычисляют среднее весовое значение дирекционного угла узловой линии по формуле
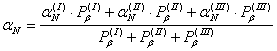
Веса получают по формуле:
![]()
где с – постоянное число, выбираемое произвольно, в данном случае с=1.
Полученное значение дирекционного угла узлового направления рассматривают как твёрдое и вычисляют невязки по ходам:
![]()
Эти невязки распределяют поровну (с противоположным знаком) на каждый измеренный угол звена и находят первые поправки к углам и вычисляют уравненное значение углов.
Таблица 3 – Вычисление средневесового значения дирекционного угла
| № хода | Вес Р | Значение дирекционного | Средневесовое значение | f β | Pβ*fβ2 | ||||
| 1/n+1 | угла узловой точки | дирекционного угла | |||||||
| 1 | 0,1667 | 60 | 24 | 57 | -9 | 12,041667 | |||
| 2 | 0,1429 | 60 | 25 | 4 | 60 | 25 | 6 | -2 | 0,3214286 |
| 3 | 0,1429 | 60 | 25 | 17 | 11 | 18,565714 | |||
| Сумма | 0,4524 | 30,9288 | |||||||
По уравненным значениям дирекционных углов вычисляют приращения координат по формулам:
![]() ,
, ![]()
где ![]() - уравненный дирекционный угол
- уравненный дирекционный угол
![]() - горизонтальное проложение. Затем вычисляют средневесовое значение координат узловой точки по формуле:
- горизонтальное проложение. Затем вычисляют средневесовое значение координат узловой точки по формуле:
![]()
![]()
Веса вычисляют по формуле:
![]()
где с – постоянное число, выбираемое произвольно.
Результаты записаны в таблице 4 для значения координаты Х и в таблице 5 для значения координаты У.
Таблица 4 – Вычисление средневесового значения координаты Х
| № хода | Вес Р | Вычисленная координата Х | Средневесовое значение | f х | Pх*fх2 | ||||
| с/[di] | узловой точки | координаты Х | |||||||
| 1 | 0,2000 | 38927,705 | -0,010 | 1,873E-05 | |||||
| 2 | 0,1667 | 38927,783 | 38927,715 | 0,068 | 0,0007615 | ||||
| 3 | 0,1667 | 38927,659 | -0,056 | 0,0005223 | |||||
| Сумма | 0,5333 | 0,0013026 | |||||||
Таблица 5 – Вычисление средневесового значения координаты У
| № хода | Вес Р | Вычисленная координата У | Средневесовое значение | f у | Pу*fу2 | ||||
| c/[di] | узловой точки | координаты У | |||||||
| 1 | 0,2000 | 36802,446 | -0,038 | 0,000291 | |||||
| 2 | 0,1667 | 36802,489 | 36802,484 | 0,005 | 4,527E-06 | ||||
| 3 | 0,1667 | 36802,525 | 0,041 | 0,0002743 | |||||
| Сумма | 0,5333 | 0,0005698 | |||||||
Похожие работы
... с ценой деления 1 сек. Области применения: построение геодезических сетей сгущения (триангуляция 4 класса, полигонометрия IV класса), в прикладной геодезии (строительство, изыскания и т.д.), астрономо- геодезических измерениях (определение азимута по Солнцу и по Полярной Звезде). Модель 3Т5КП предназначена для измерения горизонтальных и вертикальных углов и не имеет микрометра. Области ...
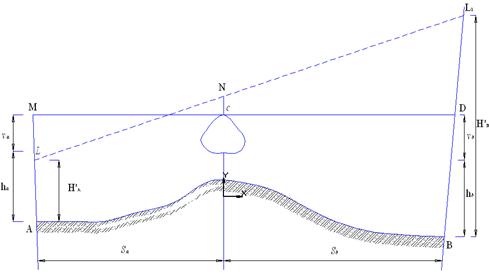
... уклонения направления сторон хода от направления замыкающей Θ, и расстояния от вершины хода до замыкающей, как следует из чертежа, меньше предельных значений. 8. Расчет точности полигонометрического хода Точность хода характеризует предельная ошибка Dпред планового положения точки в самом слабом месте после уравнивания. Учитывая, что средняя квадратическая ошибка m положения точки ...
... , тепловой и т.д.) на объект исследования. Этот тип эксперимента широко распространен в естественных науках. Обычный (классический) эксперимент включает экспериментатора как познающего субъекта; объект или предмет экспериментального исследования и средства (инструменты, приборы, экспериментальные установки), при помощи которых осуществляется эксперимент. В обычном эксперименте экспериментальные ...
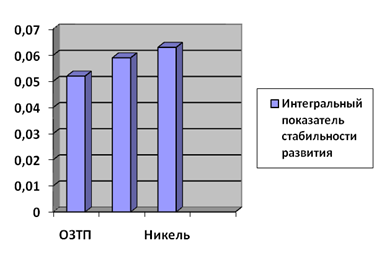
от степени техногенной загрязненности участка произростания древесных растений. Гипотеза исследования: уровень функциональной асимметрии листовой пластинки березы повислой тем выше, чем больше степень техногенной нагрузки на территории произрастания березы. Методы исследования: анализ теоретической и методической литературы, морфометрический метод, методы статистической обработки результатов ...
0 комментариев