Навигация
ТРАНСПОРТЕР КОЛОННЫ ГИБКИХ ТРУБ (ИНЖЕКТОР)
3.1. ТРАНСПОРТЕР КОЛОННЫ ГИБКИХ ТРУБ (ИНЖЕКТОР)
Кинематический расчет
Цель расчетов, приведенных в данном разделе, заключается в определении взаимосвязи скорости перемещения колонны гибких труб и подачи рабочей жидкости гидропривода к гидромоторам транспортера.
Два гидромотора, приводящие в действие цепи транспортера, получают рабочую жидкость от насоса того же типа, что и каждый гидромотор.
Подача насоса
Qф = qкnфK0/1000,
где qк – объем рабочей камеры насоса (qк = 112 см3); nф – фактическая частота вращения вала гидромотора; коэффициента подачи насоса K0 = 0,95.
При nф = 1500 об/мин Qф = 112×1500×0,95/1000 = 159,6 л/мин.
Угловая скорость вращения вала гидромотора
wг = [(Qф/2)pKом1000]/30qк,
где Kом – объемный КПД гидромотора (Kом = 0,95).
Соответственно угловая скорость вращения звездочки инжекторного механизма
wг = [(Qф/2)pKом1000]/30iqк,
где i – передаточное отношение редуктора транспортера.
Скорость подъема непрерывной трубы
v = wгR,
где R – радиус звездочки, которая приводит в действие цепь инжекторного механизма (R = 114 мм).
В результате
v = [R(Qф/2)pKом1000]/30iqк.
Скорость перемещения трубы при номинальной частоте вращения вала приводного двигателя
v = [0,114(159,6/2)×3,14×0,95×1000]/30×24×112 = 0,336 м/с.
При работе приводного двигателя с максимальной частотой вращения nф = 1800 об/мин, подача насосов Qф = 191 л/мин и соответственно скорость перемещения трубы v = 0,4 м/с.
Определение допускаемого усилия на плашки
Усилие, с которым плашки воздействуют на трубу, однозначно связано с величинами напряжений, возникающих в последней. Для определения максимально допустимого значения усилий проследим взаимосвязь внутренних силовых факторов и внешней нагрузки.
Для оценки напряжений, возникающих в продольных сечениях гибкой трубы, сжатой плашками, рассмотрим возможные варианты их взаимодействия, которые определяют картину приложения внешних сил к трубе.
В дальнейшем примем следующие допущения, которые, как показывает практика, достаточно обоснованы: плашка представляет собой абсолютно жесткий монолит, а труба – упругое тело.При взаимодействии плашек с трубой возможны три варианта приложения сил:
а) при Rтр.н < Rп возникает ситуация, изображенная на рис. 12, а;
б) при Rтр.н > Rп имеет место вариант, представленный на рис. 12, в;
в) при Rтр.н = Rп характерной является картина, изображенная на рис. 12, б.
Здесь Rтр.н – наружный радиус гибкой трубы, Rп – радиус кривизны контактной поверхности плашек.
Картины взаимодействия плашки и трубы, представленные на рис. 12, а, в, могут наблюдаться не только при несоответствии размеров трубы и плашки, но и при деформации поперечного сечения трубы. Помимо этого встречаются и другие варианты приложения нагрузки, например, несимметричный. В этом случае каждая из плашек по-своему взаимодействует с трубой.
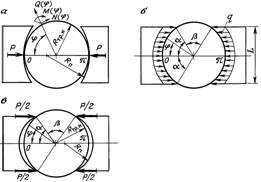
Рис. 12. Схема взаимодействия плашек транспортера с гибкой трубой:
при сжатии трубы: а – двумя сосредоточенными силами, б – равномерно распределенной нагрузкой, в – двумя парами сосредоточенных сил
Для определения наиболее опасного с точки зрения прочности трубы случая взаимодействия плашки с ее поверхностью рассмотрим внутренние силовые факторы (см. рис. 12), возникающие при различных вариантах приложения сил .
Приложение двух сосредоточенных сил. Этот случай соответствует соотношению Rтр.н < Rп (см. рис. 12, а). При этом в поперечных сечениях трубы с угловой координатой j действуют следующие силы:
нормальная
N(j) = 0,5Рsinj;
поперечная
Q(j) = 0,5Рсosj;
изгибающий момент
M(j) = РRтр.н(0,3183 – 0,5sinj).
Приложение двух пар сосредоточенных сил. Этот случай соответствует соотношению Rтр.н > Rп. Здесь также в качестве координаты рассматриваемого сечения принят угол j.
Нормальная сила:
интервал 0 £ j £ a
N(j) = –(P/2)[0,3183сosj(sin2b – sin2a)];
интервал a £ j £ b
N(j) = –(P/2)[0,3183сosj(sin2b –sin2a) + sinj];
нтервал b £ j £ p
N(j) = –(P/2)[0,3183сosj(sin2b – sin2a)].
Поперечная сила:
интервал 0 £ j £ a
Q(j) = (–P/2)[0,3183sinj(sin2a – sin2b)];
интервал a £ j £ b
Q(j) = (–P/2)[0,3183sinj(sin2a – sin2b) + сosj];
интервал b £ j £ p
Q(j) = (–P/2)[0,3183sinj(sin2a – sin2b)].
Изгибающий момент:
интервал 0 £ j £ a
M(j) = (PRтр.н/2)[0,3183(bsinb + сosb – asina – сosa –
– sin2aсosj + sin2bсosj) – sinb + sina];
интервал a £ j £ b
M(j) = (PRтр.н/2)[0,3183(bsinb + сosb – asina – сosa –
– sin2aсosj + sin2bсosj) – sinb + sinj];
интервал b £ j £ p
M(j) = (PRтр.н/2)[0,3183(bsinb + сosb – asina – сosa –
– sin2aсosj + sin2bсosj)].
В рассматриваемом случае нагружения трубы предполагают, что каждая из действующих сил равна половине усилия, приложенного к плашке.
Приложение распределенной нагрузки. Этот случай соответствует соотношению Rтр.н = Rп (см. рис. 12, б). Значение j характеризует текущую угловую координату продольного сечения, в которой определяется изгибающий момент, а a – половину угла охвата трубы плашкой. Силовые факторы в поперечных сечениях определяются следующим образом.
Нормальная сила:
интервал 0 £ j £ a
N(j) = –qRтр.нsin2j;
интервал a £ j £ p – a
N(j) = –qRтр.нsinasinj.
Поперечная сила:
интервал 0 £ j £ a
Q(j) = qRтр.нsinjсosj;
интервал a £ j £ p – a
Q(j) = qRтр.нsinaсosj.
Изгибающий момент:
интервал 0 £ j £ a
M(j) = qR2тр.н{(1/p)[(0,5a + asin2a + 1,5sinaсosa)] –
– 0,5 sin2a – 0,5sin2j};
интервал a £ j £ p – a
M(j) = qR2тр.н{(1/p)[(0,5a + asin2a) + 1,5sinaсosa] –
– 0,5sin2a – sinasinj + 0,5sin2a}.
Для определения экстремальных значений изгибающих моментов в безразмерной форме были построены эпюры, характеризующие зависимости M(j) для различных условий приложения нагрузки. Для обеспечения возможности сопоставления получаемых величин по формулам при распределенной нагрузке коэффициент выражен через величину силы P, приложенной к плашке, и ее ширину Lï = 2Rsina. Тогда
qR2тр.н = R2тр.нP/L = R2тр.нP/2Rтр.нsina = PRтр.н/2sina.
Отсюда величины безразмерных изгибающих моментов M1(j) могут быть представлены следующим образом:
при приложении двух сосредоточенных сил
M1(j) = M(j)/PRтр.н = –0,3183 + 0,5sinj;
при приложении двух пар сосредоточенных сил
интервал 0 £ j £ a
M1(j) = M(j)/2PRтр.н = (1/2)[0,3183(bsinb + сosb – asina –
– сosa – sin2aсosj + sin2bсosj) – sinb + sina];
интервал a £ j £ b
M1(j) = M(j)/2PRтр.н = (1/2)[0,3183(bsinb + сosb – asina –
– cosa – sin2aсosj + sin2bсosj) – sinb + sinj;
интервал b £ j £ p
M1(j) = M(j)/2PRтр.н = (1/2)[0,3183(bsinb + cosb – asina –
– сosa – sin2aсosj) + sin2bсosj)];
при приложении распределенной нагрузки
интервал 0 £ j £ a
M1(j) = M(j)/(PRтр.н) = [1/(2sina)]{(1/p)[(0,5a +
+ asin2a + 1,5sinaсosa] – 0,5sin2a – 0,5sin2j};
интервал a £ j £ p – a
M1(j) = M(j)/(PRтр.н/2sina) = [1/(2sina)]{(1/p)[(0,5a +
+ asin2a + 1,5sinaсosa] – 0,5sin2a – sinasinj + 0,5sin2a}.
Графики, иллюстрирующие изменение изгибающего момента, приведены на рис. 13, 14. Из них следует, что оптимальным с точки зрения минимизации напряжений, возникающих при сжатии плашкой трубы и действии распределенной нагрузки, является значение угла охвата a, близкое к 90°. Достигнуть такой величины по конструктивным соображениям невозможно, поэтому в качестве максимального значения следует принимать a = 80 ¸ 85°.
Это же положение относится и к случаю действия двух пар сосредоточенных сил. Однако этот вариант нагружения является промежуточным при переходе к распределенной нагрузке.
При условии равенства геометрических размеров поперечных сечений гибких труб для трех рассмотренных вариантов взаимодействия их с плашками наиболее опасным будет случай, при котором возникает максимальный по модулю изгибающий момент. При проведении прочностных расчетов следует, в первую очередь, учитывать растягивающие напряжения, которые суммируются с растягивающими напряжениями, возникающими при действии давления технологической жидкости.
Максимальные значения изгибающих моментов для трех рассмотренных случаев представлены ниже:
| Способ приложения нагрузки ......................................... | Две сосредоточенные силы | Две пары сосредото- ченных сил | Распределенная нагрузка |
| Максимальный изгибающий момент ............................................ | 0,318PRтр.н | 0,24PRтр.н | 0,125PRтр.н |
| Координата сечения трубы j, в которой действует максимальный момент, градус .... | 0 | 0 |
0и 90 |
|
|
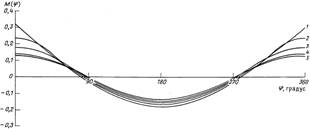
| Рис. 13. Эпюра изгибающих моментов М(j) в поперечном сечении гибкой трубы, взаимодействующей с плашками при Rтр.н < Rп: 1 – сосредоточенная сила; угол охвата трубы плашкой a, градус: 2 – 20, 3 – 40, 4 – 60, 5 – 80; j – текущая координата |
|
|
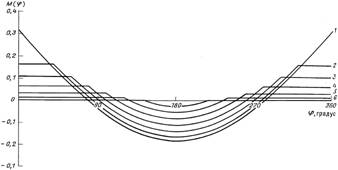
| Рис. 14. Эпюра изгибающих моментов М(j) в поперечном сечении гибкой трубы, взаимодействующей с плашками при Rтр.н > Rп: 1 – сосредоточенная сила; угловая координата точек приложения сил a, градус: 2 – 20, 3 – 30, 4 – 40, 5 – 60, 6 – 80; j – текущая координата |
Из приведенных данных следует, что наиболее предпочтительным случаем при взаимодействии трубы и плашек является приложение распределенной нагрузки. Вместе с тем, при действии двух сосредоточенных сил деформация поперечного сечения трубы приводит к увеличению площади контакта и в итоге к передаче усилия по всей площади плашки. Картина деформации поперечного сечения при приложении двух пар сосредоточенных сил является более сложной. При угле a 40 ¸ 50° они могут вызвать сплющивание трубы. Но поскольку подобные значения углов в плашках не предусмотрены, данный вопрос как представляющий сугубо теоретический интерес рассмотрен не будет.
Исходя из полученных зависимостей ,может быть вычислен изгибающий момент и определены максимальные напряжения, возникающие при обжатии трубы плашками.
Рассмотрим пример расчета напряжений в предположении, что отсутствует давление технологической жидкости во внутренней полости трубы и на нее нет осевой нагрузки.
Под действием изгибающего момента в продольном сечении гибкой трубы возникают нормальные напряжения, максимальное значение которых определяется следующим образом:
sx = Mx1/Wx1,
где Mx1 = KнагрP1R – максимальное значение изгибающего момента, действующего в поперечном сечении, в расчете на единицу длины трубы (значения максимальных моментов и соответствующих коэффициентов нагружения Kнагр приведены выше); Wx1 = bтрd2тр/6 – момент сопротивления изгибу поперечного сечения трубы, имеющей длину, равную единице (где dтр – толщина стенки трубы; bтр – ширина ее поперечного сечения, в рассматриваемом случае b = 1).
Моменты сопротивления изгибу для труб различной толщины имеют следующие значения:
| Толщина стенки трубы, dтр, мм ....................... | 2 | 2,5 | 3 | 3,5 | 4 | 5 |
| Момент сопротивления изгибу, мм3 ............ | 0,667 | 1,667 | 1,500 | 2,040 | 2,667 | 4,167 |
Максимальное усилие, приложенное к единице длины трубы, ограничено и определяется максимально допустимыми нормальными напряжениями, возникающими при изгибе за пределом упругости при образовании пластического шарнира. При расчете деталей транспортера и режимов его работы максимальное сжимающее усилие может быть установлено из условия равенства этих напряжений пределу текучести:
sx = sт = Mx1/Wx1 = KнагрP1R/Wx1.
Отсюда величина сжимающей силы P1, особенности приложения которой к трубе характеризует коэффициент Kнагр, может быть найдена из выражения
P1 = Wx1sт/KнагрR.
Значения максимальной нагрузки для наиболее распространенных размеров труб приведены ниже:
| Параметры трубы, мм: | ||||||
| наружный диаметр dтр.н | 25 | 25 | 33 | 33 | 44 | 44 |
| толщина стенки dтр .......... | 2 | 2 | 3 | 3 | 3,5 | 3,5 |
| Предел текучести sт, МПа | 480 | 700 | 480 | 700 | 480 | 700 |
| Максимальная сжимающая сила Р1, Н/мм: | ||||||
| сосредоточенная ............... | 87,5 | 127,5 | 151 | 220,2 | 153,9 | 224,4 |
| распределенная ................. | 222,7 | 324 | 383,4 | 559,2 | 390 | 570 |
| Примечание. Предел текучести 480 МПа соответствует малоуглеродистым сталям, а 700 МПа – низколегированным. | ||||||
Приведенные значения максимальной сжимающей силы P1 служат исходными данными при определении максимального тягового усилия инжектора.
Определение тягового усилия инжектора
Максимальное тяговое усилие Qmax, обеспечиваемое транспортером без проскальзывания плашек относительно гибкой трубы, определяется силой трения, действующей между ними, т.е. Qmax = Fтр.
При плоских поверхностях величину силы трения вычисляют по известной формуле
Fтр = kP,
где k – коэффициент трения между плашкой и гибкой трубой; P – усилие прижима плашки к трубе.
Однако использовать приведенную зависимость нельзя, так как контактная поверхность имеет цилиндрическую форму.
Определим силу трения, возникающую между трубой и плашкой на цилиндрической поверхности контакта (рис.15).
Элементарная сила q, приложенная к площадке dl длиной, равной единице, может быть разложена на две составляющие: нормальную к поверхности трубы qn(j) и распирающую плашку qr(j). Сила qn(j) обеспечивает создание силы трения dFтр, действующей в плоскости, перпендикулярной рассматриваемому сечению. Сила qr(j) должна быть учтена при прочностном расчете плашки.
Для площадки с координатой j можно записать
q(j) = q/сosj.
Сила трения, создаваемая на этой площадке,
dFтр = (q/сosj)kdl.
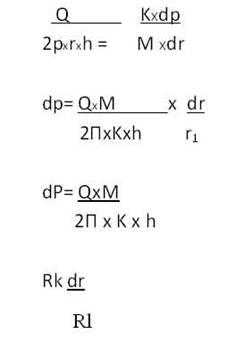
Сила трения, возникающая на поверхности трубы единичной длины, соответствующая углу a охвата ее плашкой,
![]()
Так как dl = Rтр.нdj, то при подстановке получаем
![]()
Для одной плашки высотой h это выражение будет иметь следующий вид:
Fтр1 =![]() q/сosj)kRтр.нhdj.
q/сosj)kRтр.нhdj.
В результате преобразований получим
Fтр1 = qkRтр.нh![]() 1/сosj)dj = qkRтр.нh
1/сosj)dj = qkRтр.нh![]() [(1/сosj) + tgj].
[(1/сosj) + tgj].
После подстановки значений угла получим выражение для силы трения, создаваемой плашкой на контактной поверхности при изменении угла j от нуля до максимума,
Fтр1 = qkRтр.нhln[(1/сosjmax) + tgjmax],
где jmax–половина угла охвата трубы плашкой.
Так как угол охвата трубы плашкой составляет 2jmax, то выражение будет иметь вид
Fтр1 = 2qkRтр.нhln[(1/сosjmax) + tgjmax].
В практических расчетах удобнее вычислять силу трения, обеспечиваемую парой плашек, прижатых к трубе с двух противоположных сторон. В результате значение силы трения должно быть удвоено:
Fтр1 = 4qkRтр.нhln[(1/сosjmax) + tgjmax].
Величина распределенной нагрузки q может быть определена как
q = P/hb = P/Rтр.нh2sinjmax.
После подстановки в получим
Fтр1 = 2Pkln[(1/сosjmax) + tgjmax]/sinjmax.
Таким образом, криволинейный профиль плашки в формуле для определения силы трения может быть учтен с помощью коэффициента
hф = ln[(1/сosjmax) + tgjmax]/sinjmax,
а окончательная формула примет традиционный вид:
Fтр1 = 2Pkhф.
Для упрощения расчетов можно пользоваться величиной коэффициента hф, зависящей только от угла охвата трубы плашкой jmax:
| Угол захвата трубы плашкой jmax, градус ............................................................. | 20 | 30 | 40 | 50 |
| Коэффициент hф ....................................... | 1,042 | 1,099 | 1,187 | 1,320 |
| Угол захвата трубы плашкой jmax, градус ............................................................. | 60 | 70 | 80 | 85 |
| Коэффициент hф ....................................... | 1,521 | 1,847 | 2,474 | 3,143 |
Максимальное тяговое усилие Qmax, создаваемое транспортером при перемещении трубы, определяется суммой сил трения, создаваемых плашками, находящимися в контакте с поверхностью трубы, т.е.
Qmax = SFтрn,
где n – число пар плашек.
Если усилие прижима плашек к трубе одинаковое, то максимальное тяговое усилие может быть рассчитано по формуле
Qmax = 2Pmaxkhфn.
Величина максимального усилия, прилагаемого к плашке, Pmax может быть определена исходя из условия прочности трубы, сжатой плашками.
При проектировании устройств для перемещения трубы приходится решать обратную задачу – определять необходимое число пар плашек, которые могут обеспечить заданное тяговое усилие.
Алгоритм решения этой задачи следующий:
а) исходя из геометрических размеров поперечного сечения трубы и прочностных свойств материала, из которого она изготовлена, определяют максимально допустимое усилие [Pmax], которое может быть приложено к плашкам;
б) по заданной величине тягового усилия транспортера Qmax с учетом коэффициента трения k и предполагаемого угла охвата плашками трубы устанавливают необходимое число пар плашек, которые должны быть прижаты к трубе одновременно.
Решение задачи усложнено тем, что транспортер будут использовать с колоннами гибких труб, изготовленных из материалов с различными прочностными характеристиками, поэтому его конструкция должна обеспечивать создание номинального тягового усилия для различных колонн.
Для удовлетворения этого условия число плашек следует определять, исходя из условий работы с трубой, имеющей минимальные прочностные характеристики, а размеры гидравлических цилиндров и давления в них, – исходя из максимальных значений этих характеристик:
n = Qmax/2Pmaxsminkhф.
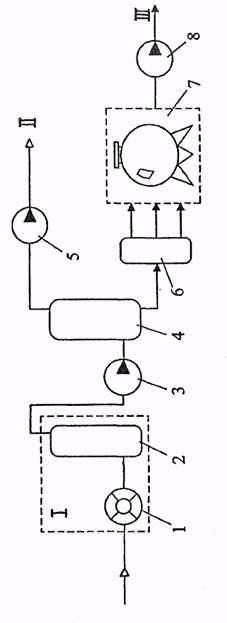
Расчет режима работы
гидропривода транспортера
Две бесконечные цепи транспортера приводятся в действие гидромоторами типа 3102.112 через планетарные редукторы. Технические характеристики гидромотора следующие:
| Объем рабочей камеры, см3 ................................................................................. | 112 |
| Номинальная частота вращения вала, об/мин ............................................ | 1500 |
| Номинальный расход жидкости, л/мин ........................................................ | 175 |
| Номинальный перепад давления для гидромотора, МПа ....................... | 20 |
| Максимальное давление на входе в гидромотор, МПа ............................ | 35 |
| Крутящий момент гидромотора, Н: номинальный ........................................................................................................ страгивания ........................................................................................................... | 342 258 |
| Номинальная мощность насоса, кВт ............................................................... | 58,4 |
| Коэффициент подачи для насоса в номинальном режиме, %, не менее .................................................................................................................................. | 95 |
| Гидромеханический КПД для гидромотора в номинальном режиме, %, не менее ................................................................................................................. | 96 |
| КПД в номинальном режиме, %, не менее: насоса ...................................................................................................................... гидромотора .......................................................................................................... | 91 92 |
| Масса без рабочей жидкости, кг, не более .................................................... | 31 |
Усилие, развиваемое транспортером, при работе двух гидромоторов при их номинальном давлении
P = 2Мкр.ном/R,
где Мкр.ном – крутящий момент на валу каждой из ведущих звездочек транспортера; R – радиус звездочки (R = 114 мм).
Момент
Мкр.ном = Мг.м.номi,
где Мг.м.ном – крутящий момент, развиваемый гидромотором, при номинальном давлении, i – передаточное число редуктора, установленного между гидромотором и звездочкой (i = 24).
При работе гидромотора с перепадом давления, отличающимся от номинального значения, крутящий момент, развиваемый гидромотором,
Мг.м = Мг.м.номРг/Рном,
где Рном – давление, соответствующее номинальному крутящему моменту на валу гидромотора; Рг – рабочее давление в гидроприводе.
Аналогичные зависимости имеют место и для страгивающего момента. Окончательно усилие, развиваемое транспортером при постоянном движении (при номинальном режиме работы гидромотора),
P = 2Мг.м.номi/R = 2×342×24/0,114 = 144 кН.
Усилие, действующее на гибкую трубу при страгивании,
P = 2Мг.м.стрi/R = 2×258×24/0,114 = 108,63 кН.
Похожие работы
... путем зарезки боковых стволов. Для бурения боковых горизонтальных стволов малого диаметра в АНК «Башнефть» начата реализация проекта по разработке и освоению технологии бурения на депрессии с применением облегченных ПЖ и колтюбингового способа бурения. Проект реализуется преимущественно на отечественном оборудовании. По заказу АНК «Башнефть» разработаны и изготовлены колтюбинговая установка, ...
... их глушения. Развитие колтюбинговых технологий, основанных на применении безшуфтовых гибких, непрерывных стальных труб обеспечивает высокую эффективность проведения операций текущего и капитального ремонта: ликвидацию отложений в скважинах, поинтервальную обработку, борьбу с обводнениями, доставку и извлечение внутрискважинного оборудования, ловильные операции и др. Сегодня в мире эксплуатируется ...
... », имея 30-летний опыт разработки и изготовления геофизических приборов для исследований бурящихся скважин, была привлечена нефтяной компанией «Башнефть» для создания технологии колтюбингового бурения наклонно-направленных и горизонтальных скважин. Так как основной объем буровых работ планируется выполнять на облегченных растворах в условиях депрессии, АНК «Башнефть» закуплена специальная ...
... месторождений от сейсморазведки до производства и ввода в эксплуатацию. Миссия ООО "ЮганскСибстрой" - быть головной организацией по научному обеспечению производственной деятельности предприятий газовой промышленности в Западно-Сибирском регионе. Основная функция - научное и проектное обеспечение развития предприятий газовой промышленности в Западной и Восточной Сибири, сокращение сроков ...

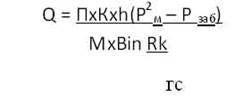
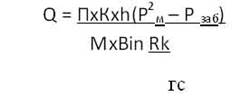






0 комментариев