Находим испарение для Ирбы

4. Находим испарение для Ирбы

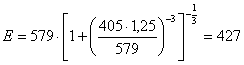 мм

Вывод: данные расчеты испарения приобретают важное значение в связи с оценкой водного баланса. В результате расчетов получили:

среднемноголетнее испарение с поверхности воды Е_в = 427 мм;

среднемноголетнее испарение с поверхности суши Е_с = 320 мм.

3. Вычисление расхода воды аналитическим способом

Цель - найти основные гидрометрические характеристики реки.

Задача: вычислить расход воды.

Исходные данные: выписка из книжки для записи измерения расхода воды на реке.

Требуется: найти ширину реки (В, м); найти среднюю скорость реки (, м/с); найти максимальную глубину (h_max, м); найти среднюю глубину (, м); найти расход воды (Q, м³/сек); найти смоченный периметр (ψ, м); найти гидравлический радиус (R, м); найти максимальную скорость реки (V_max, м/сек); найти площадь живого сечения (ω, м²).

Порядок выполнения работы.

Таблица. Вычисление расхода воды аналитическим способом

№ вертикалей		Расстояние от постоянного начала, м	Глубина, м		Расстояние между промерными вертикалями	Площадь живого сечения, м2		Средняя скорость, м/c		Расход воды между скоростными вертикалями
Промерных	Скоростных		Средняя	между промерными вертикалями		между промерными вертикалями	между скоростными вертикалями	на вертикали	между скоростными вертикалями
1	2	3	4	5	6	7	8	9	10	11
Урез пб		2	0
				0,39	2	0,78
1		4	0,78				3,44		0,39	1,35
				1,33	2	2,66
2	I	6	1,88
				2,09	2	4,18		0,56
3		8	2,3
				2,37	2	4,74	14,01		0,65	9,04
4		10	2,44
				2,55	2	5,09
5	II	12	2,65
				2,44	2	4,87		0,73
6		14	2,22				9,16		0,70	6,41
				2,15	2	4,29
7	III	16	2,07
				1,99	2	3,97		0,67
8		18	1,9
				1,78	2	3,55	11,40		0,47	5,35
9		20	1,65
				0,83	4,7	3,88
Урез лб		24,7	0					0,0
						38,01	38,01			22,14

Столбцы 1, 2, 3, 4, 9 - известны.

Столбец 5 - глубина между промерными вертикалями - среднее значение между средними глубинами на урезе правого берега и первой промерной вертикалью и так далее.

Столбец 7 - площадь между промерными вертикалями - произведение столбца 5 - глубина между промерными вертикалями, и столбца 6 - расстояние между промерными вертикалями.

Столбец 8 - площадь между скоростными вертикалями - сумма площадей между соответствующими промерными вертикалями. Общая площадь водного сечения получена как сумма частичных площадей между промерными или скоростными вертикалями.

Столбец 10 - скорость между скоростными вертикалями - между урезами воды и первой или последней промерной вертикалью это произведение средней скорости на вертикали и коэффициента 0,7; между остальными скоростными вертикалями - их среднее значение.

Столбец 11 - расход воды между скоростными вертикалями -произведение значений столбца 8 - площадь сечения между скоростными вертикалями, и столбца 10 - средняя скорость между скоростными вертикалями. Общий расход определяется как сумма всех расходов между скоростными вертикалями. Ширина реки - расстояние между геодезическим прибором и урезом левого берега вычесть расстояние между геодезическим прибором и урезом правого берега:

В = 24,7 м - 2 м = 22,7 м

 

Средняя скорость реки определяется по формуле:

Среднюю глубину реки находим с помощью выражения:

Смоченный периметр - ломаная линия по дну реки. Смоченный периметр всегда больше ширины реки (Ψ>В).

 

В нашем случае: ψ₁=2,15 м, ψ₂=2,28 м, ψ₃=2,04 м, ψ₄=2,00 м, ψ₅=2,01 м, ψ₆=2,05 м, ψ₇=2,01 м, ψ₈=2,01 м, ψ₉=2,02 м, ψ₁₀=4,98 м

Гидравлический радиус определяем по формуле:

Выводы: из работы видно, что:

расход воды на реке (Q) равен 22,14 м³/сек;

площадь водного сечения (ω) - 38,01 м²;

ширина реки (В) - 22,7 м.;

средняя глубина () - 1,67 м.;

максимальная глубина (h_max) - 2,65 м.;

средняя скорость течения () - 0,58 м/сек;

максимальная скорость (V_max) - 0,73 м/сек;

смоченный периметр (ψ) - 23,55 м.;

гидравлический радиус (R) - 1,61 м.

4. Расчёт годового стока

Цель: изучить закон вероятности гамма-распределения.

Задачи: построить эмпирическую кривую; найти статистические параметры ряда; построить аналитические кривые обеспеченности гамма-распределения.

Задание 1 Построение эмпирической кривой обеспеченности среднегодовых расходов воды.

Исходные данные: среднегодовые расходы воды на реке по данным наблюдений за 28 лет.

Требуется: построить эмпирическую кривую обеспеченности среднегодовых расходов воды.

Порядок выполнения работы.

Чтобы построить эмпирическую кривую нужно заполнить таблицу.

Таблица 1 Вычисление эмпирической обеспеченности среднегодовых расходов воды

№ п/п	Год	Q, м³/сек	Кi	P	Kp	Рг
1	1957	15,2	0,63	3,45	1,57	2,09
2	1958	19,4	0,80	6,90	1,39	6,81
3	1959	33,9	1,39	10,34	1,36	8,53
4	1960	28,2	1,16	13,79	1,31	11,10
5	1961	28,4	1,17	17,24	1,28	13,05
6	1962	25,7	1,06	20,69	1, 20	20,06
7	1963	26,4	1,09	24,14	1,17	23,51
8	1964	20,5	0,84	27,59	1,16	24,44
9	1965	21	0,86	31,03	1,09	33,78
10	1966	31,2	1,28	34,48	1,06	37,88
11	1967	24,7	1,02	37,93	1,06	37,88
12	1968	13,5	0,56	41,38	1,05	39,09
13	1969	33	1,36	44,83	1,02	43,47
14	1970	16,7	0,69	48,28	1,02	44,11
15	1971	23,2	0,95	51,72	0,98	49,99
16	1972	24,8	1,02	55,17	0,95	54,01
17	1973	31,9	1,31	58,62	0,95	54,68
18	1974	21,5	0,88	62,07	0,95	55,36
19	1975	29,2	1, 20	65,52	0,88	65,40
20	1976	13,1	0,54	68,97	0,86	68,65
21	1977	25,7	1,06	72,41	0,85	70,56
22	1978	23,1	0,95	75,86	0,84	71,82
23	1979	23	0,95	79,31	0,80	78,34
24	1980	23,8	0,98	82,76	0,78	80,53
25	1981	20,7	0,85	86,21	0,69	90,77
26	1982	19	0,78	89,66	0,63	95,10
27	1983	38,2	1,57	93,10	0,56	98,01
28	1984	25,5	1,05	96,55	0,54	98,44
		Qср = 24,30

Модульный коэффициент К_i находим по формуле:

Для каждого модульного коэффициента вычисляем соответствующую ему эмпирическую обеспеченность Р по формуле:

В последнем столбце располагаем ранжированные в порядке убывания значения модульных коэффициентов К_р.

Эмпирическая кривая представляет собой зависимость К_р от Р.

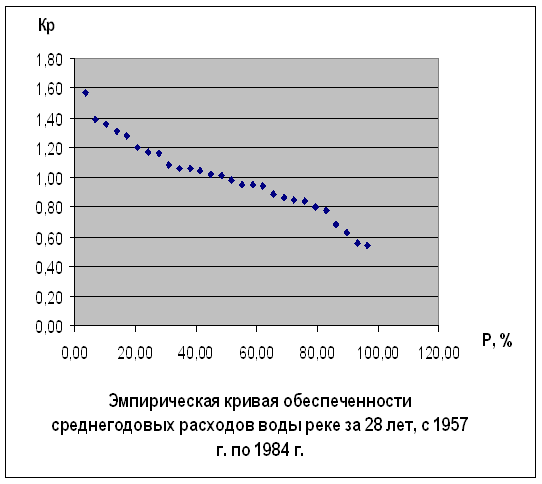
Задание 2. Определение статистических параметров ряда.

Исходные данные: среднегодовые расходы воды на реке по данным наблюдений за 28 лет.

Требуется: найти среднеарифметическое ; отклонение σ; коэффициент асимметрии с_s; коэффициент вариации с_v.

Порядок выполнения работы.

Находим статистические параметры.

Таблица 2 Статистические параметры

Среднее	24,3
Стандартная ошибка	1,2
Медиана	24,3
Мода	25,7
Стандартное отклонение	6,1
Дисперсия выборки	37,7
Эксцесс	-0,1
Асимметричность	0,2
Интервал	25,1
Минимум	13,1
Максимум	38,2
Сумма	680,5
Счет	28,0

Из последней таблицы следует:

среднеарифметическое Q_i:

 м³/сек;

 

стандартное отклонение σ:

 м³/сек;

 

коэффициент асимметрии С_S:

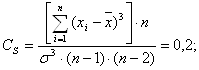
коэффициент вариации С_V:

Задание 3. Построение аналитических кривых обеспеченности гамма-распределения.

Исходные данные: эмпирическая обеспеченность и ранжированный в порядке убывания модульный коэффициент.

Требуется: построить аналитическую кривую обеспеченности и вычислить расход воды при 75-процентной и 95-процентной обеспеченности при гамма-распределении.

Порядок выполнения работы.

Для построения аналитических кривых заполняем таблицу ниже.

Таблица 3

Kp	P	Рг
1,57	3,45	2,09
1,39	6,90	6,81
1,36	10,34	8,53
1,31	13,79	11,10
1,28	17,24	13,05
1, 20	20,69	20,06
1,17	24,14	23,51
1,16	27,59	24,44
1,09	31,03	33,78
1,06	34,48	37,88
1,06	37,93	37,88
1,05	41,38	39,09
1,02	44,83	43,47
1,02	48,28	44,11
0,98	51,72	49,99
0,95	55,17	54,01
0,95	58,62	54,68
0,95	62,07	55,36
0,88	65,52	65,40
0,86	68,97	68,65
0,85	72,41	70,56
0,84	75,86	71,82
0,80	79,31	78,34
0,78	82,76	80,53
0,69	86,21	90,77
0,63	89,66	95,10
0,56	93,10	98,01
0,54	96,55	98,44

 

К_р - ранжированный в порядке убывания модульный коэффициент. Р - эмпирическая обеспеченность.

Р_Г - значения обеспеченности при гамма-распределении, которое определяется формулой:

;

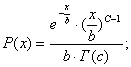
Для нахождения Р_Г в Excel пользуемся функцией ввода формул: гаммарасп. При этом x - первое значение k_p; альфа - ; бетта = ; интегральное - 1.

Пользуясь диаграммой, расположенной ниже, мы находим значение расхода воды при 75-процентной и 95-процентной обеспеченности, но данные значения не совсем точные, поэтому для определения расхода воды при 75-процентной и 95-процентной обеспеченности пользуемся следующими формулами:

 

Теперь мы находим К_75Г и К_95Г. Получаем, что: К_75Г=0,82, а К_95Г=0,63.

Следовательно:

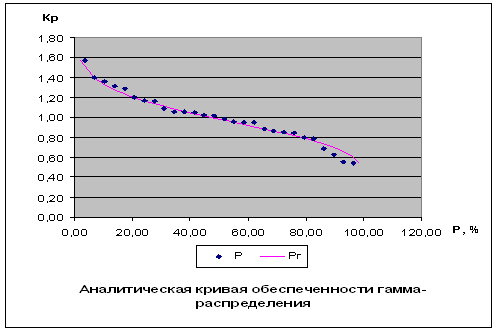
Выводы: используя данные значения, мы построили эмпирическую кривую обеспеченности, а также аналитическую кривую обеспеченности при гамма-распределении среднегодовых расходов воды реке. Нашли расход воды при 75-процентной и 95-процентной обеспеченности гамма-распределения: Q_75Г = 19,93 м³/сек, Q_95Г = 15,31 м³/сек. Также получили статистические параметры:

среднеарифметическое	24,3
отклонение σ	6,1
коэффициент асимметрии сs	0,2
коэффициент вариации сv	0,25

Заключение

Из первой выполненной работы имея данные: площадь водосбора - 9320 км², расход воды - 24,3 м³/сек, высота годового слоя осадков - 405 мм, мы получили следующие характеристики водности рек:

модуль стока - 2,61 л/с∙км²;

высота слоя стока - 82,22 мм;

объем годового стока - 0,77 м³;

коэффициент стока - 0, 203.

Последний показатель отражает, в районе с какой влажностью находится пункт наблюдения, в данном случае с. Ирба. Исходя из полученных данных можно сказать, что район относится к засушливым, так как в таких районах коэффициент стока уменьшается до нуля, а в районах избыточного увлажнения возрастает до 0,7. В данном случае ɳ=0, 203.

Во второй работе данные расчеты испарения приобретают важное значение в связи с оценкой водного баланса. В результате расчетов получено:

среднемноголетнее испарение с поверхности воды Е_в = 427 мм;

среднемноголетнее испарение с поверхности суши Е_с = 320 мм.

Из третьей работы видно, что:

расход воды на реке равен 22,14 м³/сек;

площадь водного сечения - 38,01 м²;

ширина реки - 22,7 м.;

средняя глубина - 1,67 м.;

максимальная глубина - 2,65 м.;

средняя скорость течения - 0,58 м/сек;

максимальная скорость - 0,73 м/сек;

смоченный периметр - 23,55 м.;

гидравлический радиус - 1,61 м.

В четвертой работе используя данные значения, мы построили эмпирическую кривую обеспеченности, а также аналитические кривые обеспеченности при гамма-распределении среднегодовых расходов воды. Нашли расход воды при 75 - и 95-процентной обеспеченности гамма-распределения: Q_75Г = 19,93 м³/сек, Q_95Г = 15,31 м³/сек.

Список использованной литературы

1.  Гидрология, гидрометрия и регулирование стока: Учебники и учебные пособия для высших сельскохозяйственных учебных заведений/ Г.В. Железняков, Т.А. Неговская, Е.Е. Овчаров. - М. "Колос", 1984.

2.  Практикум по гидрологии, гидрометрии и регулированию стока: Учебники и учебные пособия для студентов высших учебных заведений/ под редакцией Е.Е. Овчарова. - М. ВО"Агропромиздат", 1988.

3.  Статистика с применением Exsel: Учебное пособие. / Под ред. Я.М. Иваньо, А. Ф Зверева. - Иркутск, 2006. - 137 с.