Навигация
2.3 Завдання 2.1
Задача А.
Вирішити задачу проектування конусоподібного фільтра.
Із круглої заготівлі (r = 2) фільтрованого паперу вирізують сектор з кутом 
, потім з іншого роблять фільтр у вигляді конуса. Необхідно розрахувати величину кута , при якій забезпечується максимальний об'єм конуса.
R - радіус основи конуса; h - висота конуса; r - радіус заготівлі фільтрованого паперу.
Рішення засобами Excel
Спочатку ми задаємо цільову функцію, потім визначаємо для неї обмеження, вибираємо змінювані змінні та, задавши перші наближення для змінних, виконуємо Пошук рішення.
Як цільова функція виберемо рівняння об'єму конуса умови незаперечності змінних величин, і кут Q не повинен перевищувати 2 ПІ .
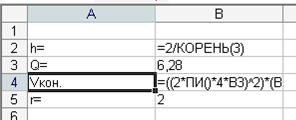
Рисунок 2.14 - Дані в режимі відображення формул
Застосувавши Пошук рішення:
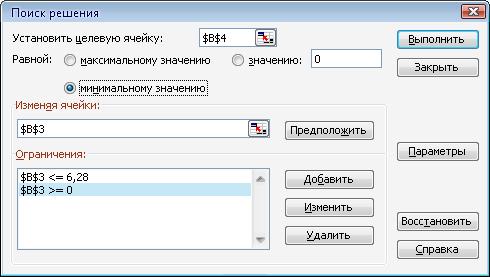
Рисунок 2.15 - Вікно пошуку рішення
При натисканні клавіші "Виконати" на екрані з'являється наступне вікно й таблиця з рішенням (рис. 2.16):
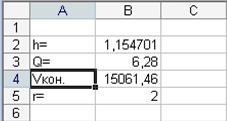
Рисунок 2.16 - Результат рішення
Рішення засобами MathCAD.
Задача зведена до максимізації функції однієї змінної.
Максимум цільової функції можна знайти, використовуючи:
Потужним способом MathCAD для рішення оптимізаційних задач є використання вбудованих функцій Minimize та Maximize. Функція Maximize використовується у вигляді:
Maximize (цільова функція, параметр1, параметр2, ..., параметрN )
Вирішимо нашу задачу використовуючи функцію Maximize
Висновок: Отримані в результаті обчислень різними програмними продуктами (MathCAD ,Excel) значення повністю ідентичні, що говорить про вірогідність рішення. Так само наочно видно, що обчислення в MathCAD більше громіздкі, але з математичної точки зору більше правильні.
Задача Б.
Проектування 2 -х конусоподібних (пожежних) цебер.
Із круглої заготівлі жерсті (r = 3) вирізують сектор з кутом , потім з іншого роблять цебро у вигляді конуса й з вирізаного сектора теж (тобто 2-а цебра). Необхідно розрахувати величину кута θ, тобто Як необхідно розкроїти заготівлю, щоб об'єм 2-х цебер був максимальним.
R -радіус основи конуса; h - висота конуса; r - радіус заготівлі
Рішення засобами Excel.
Для рішення даної задачі необхідно заповнити таблицю з вихідними даними й розрахунковими формулами (рис. 2.17).
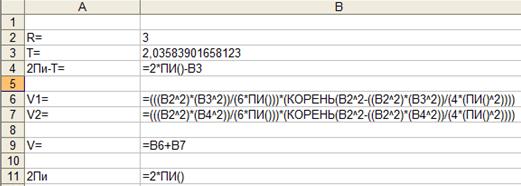
Рисунок 2.17 - Дані в режимі відображення формул
Об'єм першого сектора розраховується по формулі:
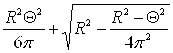
Об'єм другого сектора розраховується по формулі:
Далі задається початкове значення кута 
=0, установлюється цільовий осередок (загальний об'єм). Викликається "Пошук рішень" (рис. 2.17). Тому що це коло, то обмеження для кута наступні: 
.Нижче наведені відповідні таблиці .
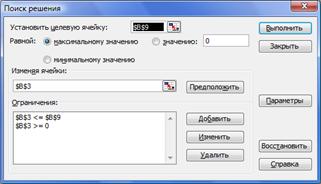
Рисунок 2.18- Вікно пошуку рішень
Виконавши даної операції, було отримано наступне рішення (рис. 2.19, 2.20).
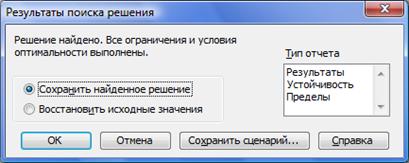
Рисунок 2.19 – Вікно результату пошуку рішень
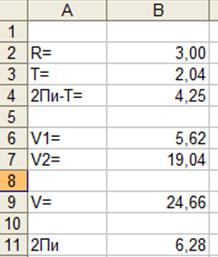
Рисунок 2.20 - Результат рішення
Рішення засобами MathCAD
Для рішення даної задачі необхідно заповнити таблицю з вихідними даними й розрахунковими формулами, представленими вище.
А далі скористаємося вже відомою структурою Given.
Висновок: Отримані в результаті обчислень різними програмними продуктами (Excel, MathCAD) значення повністю ідентичні, що говорить про вірогідність правильного рішення.
Задача 4
Для зберігання пального потрібно спроектувати бак (див. Рис). Готовий бак має вигляд циліндра з конічними переднім і заднім днищами . Обсяг бака 1 м2. Потрібно виготовити бак з мінімальної кількості матеріалу. Які повинні бути значення L1, L2, B , щоб виконувалася ця вимога.
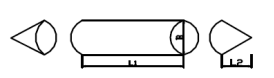
Рисунок 2.21
Рішення засобами Excel
Рисунок 2.22 - Таблиця початкових даних
Рисунок 2.23 - Дані в режимі відображення формул
Далі необхідно скористатися вікном "Пошук рішення".
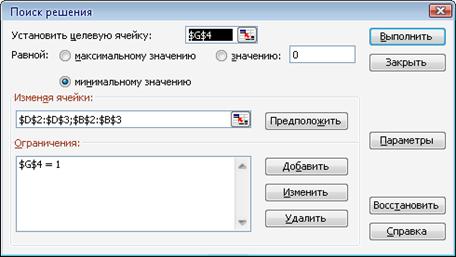
Рисунок 2.24 - Вікно пошуку рішень
Рисунок 2.25 - Результати рішення
Результат: R=0.28 h=0.28 l=0.28
Похожие работы
... ірки результату треба підставити значення отриманих змінних у вихідне рівняння. Рисунок 2.13 – Перевірка рішення системи нелінійних рівнянь Результат: х=2,188, у=-0,092. 2.3 Завдання 2.1 Задача А. Вирішити задачу проектування конусоподібного фільтра. З круглої заготівлі (r = 2) фільтрованого паперу вирізають сектор з кутом , потім з іншого роблять фільтр у виді конуса. Необхідно ...
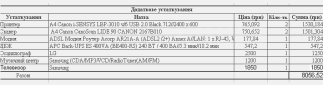
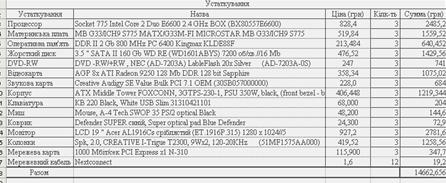
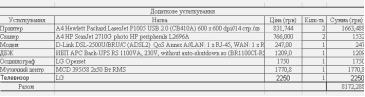
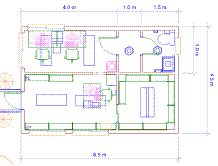
... проектування. СИСТМЕМА АВТОМАТИЗОВАННОГО ПРОЕКТУВАННЯ, ГРАФІЧНЕ МОДЕЛЮВАННЯ, МАТЕМАТИЧНЕ МОДЕЛЮВАННЯ, ОПТИМІЗАЦІЯ, ОПТИМАЛЬНІСТЬ. ЗМІСТ ВСТУП 1. ГРАФІЧНЕ МОДЕЛЮВАННЯ ОФІСУ МОБІЛЬНОГО ЗВ’ЯЗКУ 1.1 Початкові дані для проектування офісу 1.2 Опис призначення офісу та його програмне забезпечення 1.3 Співробітники офісу 1.4 Альтернативне комп'ютерне устаткування 1.5 План офісу та його ...
... проектування. СИСТМЕМА АВТОМАТИЗОВАННОГО ПРОЕКТУВАННЯ, ГРАФІЧНЕ МОДЕЛЮВАННЯ, МАТЕМАТИЧНЕ МОДЕЛЮВАННЯ, ОПТИМІЗАЦІЯ, ОПТИМАЛЬНІСТЬ. ЗМІСТ ВСТУП 1. ГРАФІЧНЕ МОДЕЛЮВАННЯ ОФІСУ БЮРО ПОСЛУГ 1.1 Початкові дані для проектування офісу 1.2 Опис призначення офісу та його програмне забезпечення 1.3 Співробітники офісу 1.4 Альтернативне комп'ютерне устаткування 1.5 План офісу та його об'є ...
... 1.2 8 Завдання 2.1 (А,Б, варіант) Ємність для поливу газона 7 Завдання 2.2 27 1.2 Опис призначення офісу і його програмне забезпечення Ця установа призначена для роботи в сфері видавництва, необхідні наступні кадри: головний редактор, 2 оператори ПК, секретар. Офіс може виконувати: o Створення учбової, учбово-методичної літератури, яка відповідає потребам державних стандартів осв ...
0 комментариев