Построение модели в стандартизированном виде

5. Построение модели в стандартизированном виде

По характеру изменения уровней фондоотдачи можно выдвинуть гипотезу о прямолинейном законе распределения этого показателя во времени. Уравнение множественной регрессии для прямолинейной связи имеет следующий вид:

.

Для решения этого уравнения регрессии воспользуемся методом исключения (методом Гаусса), для чего составим и запишем систему нормальных уравнений:

Решить систему нормальных уравнений – значит, найти численное значение коэффициентов регрессии , , . Все остальные параметры системы уравнений (коэффициенты парной корреляции) уже были вычислены на первом и втором этапах расчетов. Запишем эту же систему уравнений с численными значениями известных параметров:

Разделим каждый член каждого уравнения системы на соответствующие коэффициенты при .

В результате этой процедуры (деления) получим новую систему уравнений с тремя неизвестными, в которой коэффициенты при , равны единице:

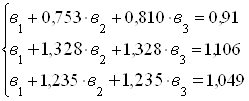
Для исключения из системы уравнений неизвестного параметра  вычтем из второго уравнения – первое, и из третьего уравнения – первое. В результате этой операции (вычитания) получим новую систему из двух уравнений, но уже только с двумя неизвестными:

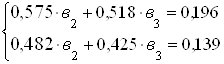
Как и в предыдущем случае, разделим каждый член каждого уравнения этой системы на соответствующие коэффициенты при .

В результате этой процедуры (деления) получим новую систему, состоящую из двух уравнений с двумя неизвестными, в которой коэффициенты при  равны единице:

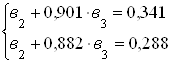
Для исключения из этой системы уравнений неизвестного параметра  вычтем из второго уравнения первое. В результате этой операции (вычитания) получим новое уравнение, но уже только с одним неизвестным:

.

Откуда

Для определения численного значения коэффициента регрессии  подставим найденное значение коэффициента регрессии  в первое уравнение системы из двух уравнений:

;

Откуда

Для определения численного значения коэффициента регрессии  подставим найденные значения коэффициентов регрессии  и  в первое уравнение системы из трех уравнений:

;

;

Откуда

Все численные значения коэффициентов множественной регрессии найдены. Тогда уравнение связи в стандартизированном виде будет иметь следующий вид:

.

6. Построение модели в натуральных единицах измерения

Для объективного анализа показателей изучаемого социально-экономического явления необходимо перейти от абстрактной стандартизированной модели к математической модели в натуральных единицах измерения. Уравнение множественной регрессии для прямолинейной связи имеет следующий вид:

Для решения этого уравнения регрессии необходимо определить численные значения коэффициентов эластичности b₁, b₂, b₃. Для этого воспользуемся следующей формулой:

,

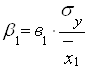где  – среднеквадратическое отклонение результирующего признака, которое определяется по формуле

.

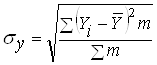Для расчета среднеквадратического отклонения и коэффициентов эластичности необходимо провести некоторые промежуточные расчеты, результаты которых представлены в табл. 5.

Таблица 5 Промежуточные расчеты для вычисления cреднеквадратического отклонения

№
46	65,200	-0,417	0,1739
47	65,200	-0,417	0,1739
48	65,300	-0,317	0,1005
49	65,400	-0,217	0,0471
50	65,500	-0,117	0,0137
51	65,600	-0,017	0,0003
52	65,700	0,083	0,0069
53	65,700	0,083	0,0069
54	65,800	0,183	0,0335
55	65,900	0,283	0,0801
56	66,000	0,383	0,1467
57	66,100	0,483	0,2333
Итого:	787,400		1,0167

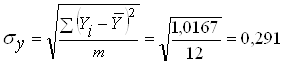
Тогда

; ; .

;

;

.

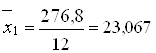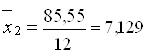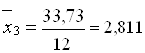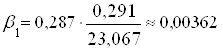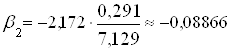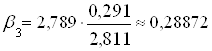В связи с тем что в формулы расчета коэффициентов эластичности входят значения , ,  с тремя десятичными знаками, а также численные значения коэффициентов эластичности малы, их следует округлить до пятого десятичного знака, чтобы модель более точно отображала результаты моделирования и прогнозирования.

Тогда уравнение множественной регрессии для прямолинейной связи для изучения фондоотдачи будет иметь следующий вид:

В этом уравнении регрессии его свободный член  является неизвестной величиной. Для определения численного значения  необходимо в это уравнение подставить средние значения результирующей и факторных величин. Тогда уравнение примет вид:

или

.

Тогда экономико-математическая модель изучаемого явления в натуральных единицах измерения будет иметь следующий окончательный вид:

.

Это уравнение регрессии необходимо проверить по двум критериям: по сходству сумм расчетных и экспериментальных значений фондоотдачи и по коэффициенту множественной корреляции.

Вычислим расчетные значения фондоотдачи по всем периодам времени:

;

;

;

;

;

;

;

;

;

;

;

.

Сумма всех расчетных значений фондоотдачи равна 787,40368 и совпадает с суммой эмпирических значений этого показателя, т.е. выполняется условие:

SY _эi = 787,4 » SY_рi = 787,40368,

следовательно, по этому критерию можно сделать вывод о правильности построения экономико-математической модели хозяйственной деятельности предприятия.

Вычислим численное значение коэффициента множественной корреляции по формуле:

= 0,91.

Так как численное значение коэффициента множественной корреляции R превышает численное значение любого из парных коэффициентов корреляции , , , а также не превышает единицы, можно сделать вывод о правильности построения экономико-математической модели хозяйственной деятельности фермерского хозяйства и по этому критерию.

Таким образом, гипотеза о прямолинейной связи между показателями рассматриваемой системы верна, и полученное уравнение множественной регрессии может использоваться в качестве модели для анализа и прогнозирования хозяйственной деятельности предприятия.