Навигация
Удаляются все строки, которые покрывает полученный столбец
3. Удаляются все строки, которые покрывает полученный столбец.
Данные действия продолжаются до тех пор, пока не удалится вся матрица.
Итого получим покрытие {3,4}-столбцовое покрытие исследуемой матрицы.
4. Метод предварительного редуцирования булевой матрицы
При поиске кратчайшего покрытия целесообразно уменьшить матрицу, если такое возможно. Можно удалить как определенные строки, так и определенные столбцы. Отметим, что в практических задачах не требуется найти все кратчайшие покрытия, достаточно только одно или несколько. Это упрощает алгоритм упрощения (сокращения) матрицы.
1. Говорят, что i-я строка булевой матрицы поглощает j-ю строку этой матрицы (![]() ), если на позициях единиц j-й строки в i-й – тоже «единицы», причем число единиц в i-й строке больше числа единиц в j-й строке (если же число единиц одинаково, то данные строки называются равными).
), если на позициях единиц j-й строки в i-й – тоже «единицы», причем число единиц в i-й строке больше числа единиц в j-й строке (если же число единиц одинаково, то данные строки называются равными).
Аналогичное утверждение можно сформировать и для столбцов.
2. Говорят, что i-й столбец булевой матрицы поглощает j-й столбец этой матрицы (![]() ), если на позициях единиц j-го столбца в i-м – тоже единицы, причем число единиц в i-м столбце больше числа единиц в j-м столбце (если же число единиц одинаково, то данные столбцы называются равными).
), если на позициях единиц j-го столбца в i-м – тоже единицы, причем число единиц в i-м столбце больше числа единиц в j-м столбце (если же число единиц одинаково, то данные столбцы называются равными).
Алгоритм: удаляются все строки, которые могут быть поглощены какими-либо другими строками матрицы, и столбцы, которые могут поглотить какие-либо другие столбцы этой матрицы, из равных строк и столбцов оставляют по одному, остальные тоже удаляют, затем в полученной матрице делаются аналогичные действия, и так до тех пор, пока матрицу нельзя будет дальше сократить.
Замечание: при реализации данного алгоритма на ЭВМ программа не удаляет строки (столбцы), что приводит к требующему ресурсы процессора созданию новых массивов, а «зануляет» их, затем игнорируя.
При поиске кратчайших покрытий предварительно сокращенной матрицы некоторые кратчайшие покрытия теряются, но это не имеет практической ценности, но объем вычислений сокращается.
Пример 4. Пусть дана булева матрица A (10 х 10):
1 2 3 4 5 6 7 8 9 10
 .
.
Удаляем строки б и е (поглощаются строкой к), строки в, д, ж (поглощаются строкой и) и строку з (поглощается строкой г). Получим матрицу ![]() , уже меньшую по размерам:
, уже меньшую по размерам:
1 2 3 4 5 6 7 8 9 10
 .
.
Удаляем столбец 1 (поглощает любой другой столбец), столбцы 2, 8 и 10 (поглощают столбец 4), столбцы 3 и 7 (равны столбцу 9) и столбец 6 (равен столбцу 4). В итоге получаем матрицу ![]() (4 х 3):
(4 х 3):
4 5 9
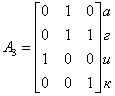 .
.
Удаляем строки а, к (поглощаются строкой г). Получаем матрицу ![]() ( 2 х 3 ):
( 2 х 3 ):
4 5 9
![]() .
.
Из последней матрицы удаляем столбец 9 (равен столбцу 5) и получаем не упрощаемую матрицу ![]() ( 2 х 2 ):
( 2 х 2 ):
4 5
![]() .
.
Единственное покрытие последней матрицы – она сама. Итого, строки г и и составляют одно из кратчайших (даже единственное) покрытий матрицы A.
5. ПРОГРАММА
Написанная мной на ЭВМ программа «Нахождение кратчайшего покрытия булевых матриц» помогает вручную не искать покрытие заданной или генерируемой булевой матрицы до размера 99 х 99, а предоставить это компьютеру.
5.1 Описание программы
Средство программирования:
Интегрированная Среда Разработки Borland C++ Builder 6.0.
Поддерживаемые операционные системы:
Windows 95/98/ME/NT/2000/XP.
Система для тестирования программы:
Pentium-4 ~2.3 Gh, 512 Mb DDR, Windows XP SP2.
5.2 Описание интерфейса
Pokrytie.exe – откомпилированная и отлаженная программа. При запуске отображается окно дополнительной информации:
При нажатии двойным щелчком на кнопку «Программа» в окне появляется основная форма — Меню программы (рис. 1).


Рис.1. Меню программы Рис.2. Задание вероятности единицы
Требуется ввести число строк и столбцов матрицы, а также выбрать тип создания требуемой матрицы: вручную или автоматически (с помощью компьютера). В первом случае возможны 2 способа создания пустого шаблона матрицы: все поля – либо нули, либо единицы (для реализации необходимо это просто отметить). Во втором же должна быть введена вероятность создания единицы в определенном месте матрицы (рис. 2).
По умолчанию все элементы матрицы – нули и программа допускает присутствие в матрице нулевых строк и столбцов. Если вы не ввели параметры матрицы до конца, то при нажатии кнопки «Сгенерировать» программа сообщит вам об этом:

При правильном вводе данных и нажатии кнопки генерации на экране появляется окно ввода матрицы:

При написании программы я применила графический способ ввода элементов матрицы: внутри прямоугольника, соответствующего размерам матрицы, чтобы изменить значение определенного элемента матрицы, необходимо нажать кнопку мыши при положении курсора внутри определенного квадрата, соответствующего этому элементу. Белый цвет соответствует нулю, а цвет выделяемого текста (по умолчанию – синий) соответствует единице. Для хранения данных в программе использованы динамические матрицы, что позволяет выделять память только по мере необходимости.
5.3 Результат работы программы
Рассмотрим несколько примеров, иллюстрирующих работу программы.
5.3.1 Пример 1. Пусть дана матрица С:
1 2 3 4 5 6
 .
.
Построим для этой матрицы кратчайшие покрытия методами Патрика и Закревского (строчное и столбцовое).
Матрица C в программе:
Покрытие методом Патрика:
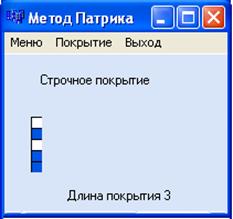
Покрытия методом Закревского

Итого, покрытия, построенные программой, совпадают с покрытиями, построенными вручную.
5.3.2 Пример 2. Построим кратчайшее покрытие для произвольной матрицы размером 7×7 с плотностью единицы 0,2 методом Патрика и методом Закревского:
Матрица, сгенерированная программой:

Покрытие методом Патрика
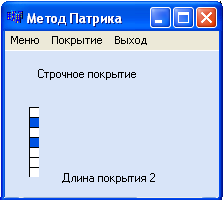
Покрытия методом Закревского

Похожие работы
... дискретного программирование для решения задач проектирование систем обработки данных. - Сформулированы задачи диссертационного исследования. 2. БЛОЧНО-СИММЕТРИЧНЫЕ МОДЕЛИ И МЕТОДЫ ПРОЕКТИРОВАНИЯ СИСТЕМ ОБРАБОТКИ ДАННЫХ В данном разделе рассматриваются общая постановка блочно-симметричной задачи дискретного программирования, её особенности и свойства. Разработан общий подход решения задач ...
... структур данных для представления в программе объектов математической модели – это основа искусства практического программирования. Далее приводится четыре различных базовых представления графов. Выбор наилучшего представления определяется требованиями конкретной задачи. Более того, при решении конкретных задач используются, как правило, некоторые комбинации или модификации указанных ...
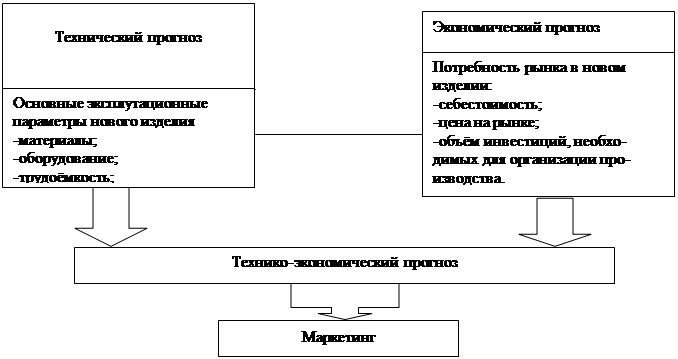
... , отвечающие определенным условиям и гипотезам, учтенным при его построении. Вместе с тем необходимо помнить, что механическое использование предиктора может стать причиной серьезных погрешностей. Экономическое прогнозирование слишком ответственное дело, для того чтобы можно было ограничиться одними формальными построениями и расчетами. Цель модели - не заменить суждения и опыт специалиста, а ...
... (ШД), адресов (ША) и управления (ШУ). Однокристальные микропроцессоры получаются при реализации всех аппаратных средств процессора в виде одной БИС или СБИС (сверхбольшой интегральной схемы). По мере увеличения степени интеграции элементов в кристалле и числа выводов корпуса параметры однокристальных микропроцессоров улучшаются. Однако возможности однокристальных микропроцессоров ограничены ...




0 комментариев