Навигация
Уравнение динамики и время трогания электромагнита постоянного тока при включении по схеме замедления процесса срабатывания (рис. 2.1,в)
2.4 Уравнение динамики и время трогания электромагнита постоянного тока при включении по схеме замедления процесса срабатывания (рис. 2.1,в)
2.4.1 Определение изменения тока и напряжения во времени численным методом
Уравнения, описывающие работу электросхемы:
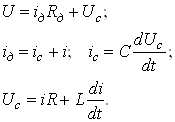
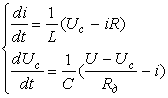
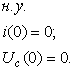
Воспользуемся функцией Rkadapt (y0, t0, t1, N, D) -получим матрицу решения системы обыкновенных дифференциальных уравнений численным методом Рунге-Кута на интервале от t0 до t1 (зададим от 0 до 5 сек) при N фиксированных шагах решения (пусть N=1000), вектор заданных начальных условий X0 (нулевые условия). Сформируем матрицу системы дифференциальных уравнений, соответствующую заданному дифференциальному уравнению 2-го порядка.
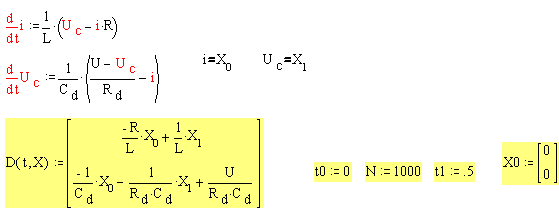 | |||
Т-нулевой столбец, i- первый столбец, Uс- второй столбец.
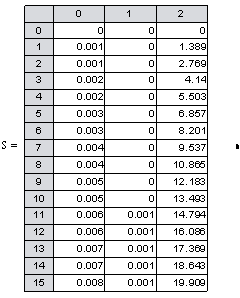
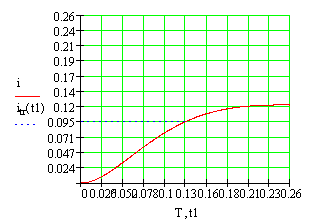
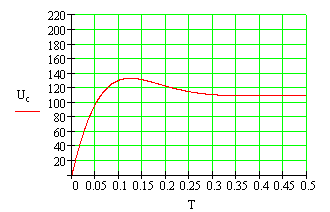
Рис.2.8. Графики зависимости тока в катушке электромагнита и напряжения на конденсаторе от времени при замедленном срабатывании электромагнита (численный метод решения дифференциальных уравнений)
2.4.1 Определение изменения тока и напряжения во времени операторным методом
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Составляем оператор. В расчётах применяется функция Mathcad identity (2) - создаёт единичную матрицу ( по диагонали стоят единицы) размером 2*2 и операция обратная матрица (-1).Для ввода оператора поиска обратной матрицы нажмём кнопку Inverse (Обратная матрица) на панели инструментов Matrix (Матрица).Применяем функцию invlaplace для обратного перехода из комплексной области.
![]()
![]()
![]()
![]()
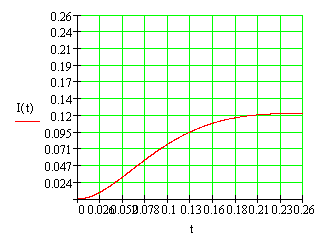
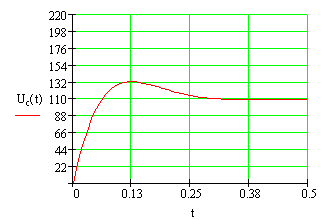
Рис.2.9. Графики зависимости тока в катушке электромагнита и напряжения на конденсаторе от времени при замедленном срабатывании электромагнита (операторный метод решения дифференциальных уравнений)
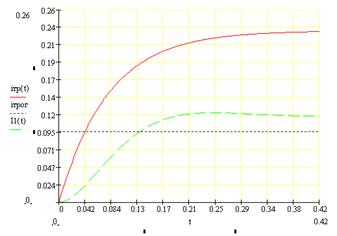
Рис. 2.10.Сравнительный анализ времени трогания по схеме прямого включения и схемы с запаздыванием.
Как видно из графиков кривая зависимости тока от времени при схеме включения с запаздыванием лежит ниже. Время трогания увеличивается с 0,042с до 0,13 сек.
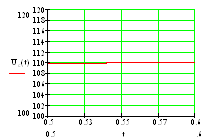
Рис.2.11. Установившееся значение напряжения на конденсаторе.
Из рис.2.11. видно, что напряжение на конденсаторе принимает установившееся значение Uс=110 В.
2.4.3. Аналитический метод определения времени трогания якоря электромагнита по графику
![]()
![]()
![]()
![]()
![]()
![]()
![]()
2.4.4 Решение с использованием передаточной функции
Передаточная функция для схемы с замедлением имеет вид:
![]() , следовательно
, следовательно
Уравнения, описывающие работу схемы:
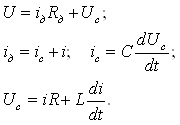
![]()
![]()
![]()
![]()
![]()
Переходим из комплексной области с помощью функции invlaplace

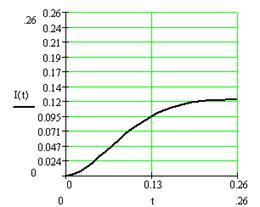
Рис.2.12. График зависимости тока от времени при замедленном срабатывании электромагнита (метод решения с помощью передаточной функции)
Заключение
Целью данной РГР является подтвердить расчетами теоретические положения расчета времени трогания электромагнитов постоянного тока, включенных по различным схемам срабатывания. Были изучены возможности математического пакета MathCad в среде Windows для решения дифференциальных уравнений, описывающих динамику электромагнитов постоянного тока. Для схем включения электромагнита при ускоренном или замедленном срабатывании были составлены системы дифференциальных уравнений в форме Коши, описывающих их работу. Системы решались с помощью функции MATHCAD Rkadapt(y0, t0, t1, N, D) — метод Рунге-Кутты с переменным шагом, так получено численное решение. Кроме того были использованы передаточные функции. При переходе из комплексной области во временную применяется обратное преобразование Лапласа (функция invlaplace). Для схемы замедления использовался также операторный метод. Решение в MATHCAD связано с операциями над матрицами. Вычисления наглядно демонстрируют графики. Графики, построенные при разных способах решения совпадают.
Результаты расчётов: время трогания электромагнита постоянного тока 0,042с и 0,1296с для схем прямого и замедленного подключения соответственно. Кривая зависимости тока от времени при схеме включения с запаздыванием лежит ниже. Ток трогания 0,095 А.
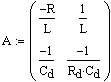
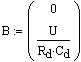
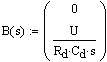
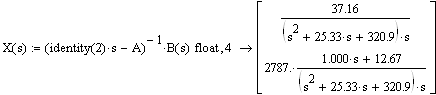
0 комментариев