J=1

0 j=1

здесь Ij(t)- доход j - го агента, "j j=1,n

R(t) можно представить в виде производственной функции.

Т.е.

R(t)=F(K1(t),K2(t),..., Kn(t), L(t)) (2.3)

Здесь Kj(t) - капитал, заработанный j - ым агентом.

Доход страхового агента можно представить как долю от величины поступивших за счет его работы страховых платежей с учетом коэффициента, характеризующего его страховое поле.(Определения, связанные со страхованием смотри в приложении 1) Все необходимые предположения для определения дохода j-го страхового агента сделаны в п.1

Ij(t)=mbjR(t), где 0<m<1, bj>0, "j j=1,n

Аналогично рассуждениям, приведенным в предыдущей модели, R(t) используется по тем же направлениям. Часть дохода страховой компании, идущая на развитие жизнедеятельности фирмы, распределяется следующим образом:

n

(1-m)R(t)=åWaj(t) +L(t)+dK(t)+ K’(t) +p(t) K(t) (2.4)

j=1

Здесь Waj(t) - затраты, связанные с процессом и обслуживанием заключения договоров страхования и средств, выделяемых администрацией j - му страховому агенту в форме отпускных и других положенных ему денежных вознаграждений.

Waj(t) = gKj(t)+CmL(t)/n "j j=1,n (2.5)

Все прочие обозначения смотрите в п.1.

Таким образом модель имеет вид:

Максимизировать

¥ n

J(t)=ò( åaIj(t) +(1-a)R(t))e^-rt dt

0 j=1

при условиях

n

(1-m)R(t)=åWaj(t) +L(t)+dK(t)+ K’(t) +p(t) K(t)

j=1

R(t)=F(K1(t),K2(t),..., Kn(t), L(t))

Ij(t)=mbjR(t), где 0<m<1, bj>0, "j j=1,n

Waj(t) = gKj(t)+CmL(t), "j j=1,n

0<g<1,0<Cm<1, 0<d<1

p(t)³pс,0<a<1,

L(0)=L₀, L₀>0,K(0)=K₀,K₀>0

п3. Многосекторная модель роста доходности страховой фирмы.

Рассматривается страховая фирма, которая предлагает n видов страхования. Каждый агент занимается только одним видом страхования, таким образом имеем n агентов. Все агенты работают на одном и том же участке.

Предполагается, что доходность фирмы складывается из договоров, заключенных агентами, т.е.

n

R(t)= åRj(t).

j=1

Верно также и соотношение (2.2)

В силу аналогичных рассуждений целевой функционал построим в виде:

¥ n n

J(t)=ò( åaIj(t)+ å(1-a)Rj(t))e^-rt dt

0 j=1 j=1

Здесь Ij(t)- доход агента, где j=1,n. Rj(t) - объем заключенных договоров j-ым агентом, в руб.

Rj(t) можно представить в виде производственной функции.

Rj(t)=F(Kj(t), L(t)), "j j=1,n. (2.6).

Из рассуждений приведенных в п.2 доход j - го страхового агента определяется по формуле

Ij(t)=mjRj(t), "j j=1,n.

Рассуждения, связанные с распределением дохода страховой компании аналогичны приведенным выше. ( п.2). Соответственно сохраняются выражения (2.4) и (2.5).

Таким образом многосекторная модель имеет вид

Максимизировать

¥ n  n

J(t)=ò( åaIj(t)+ å(1-a)Rj(t))e ^-rt dt

0 j=1 j=1

при ограничениях

Rj(t)=F(Kj(t), L(t)) "j j=1,n

Ij(t)=m jRj(t) "j,j=1,n

n

(1- m)R(t)= åWaj(t)+L(t)+K’(t)+dK(t)+p(t)K(t)

j=1

Waj(t) = gKj(t)+CmL(t) "j,j=1,n

0<g<1, 0<Cm <1, 0<d<1

0<a<1, 0<m<1, p(t)³pc

L(0)=L₀, L₀>0, K(0)=K₀, K₀>0

п.4 Дискретный аналог простейшей модели роста доходности.

Дискретным аналогом простейшей модели является следующая модель, при постановке которой использовалась идея модели Лурье [6,стр.173]

aI_T+(1-a)(R_T+p_cK_T) ® max

при ограничениях

I_t=mR_t-1-haD K_t-1 "t t=1,T

R_t=F(K_t,L_t) "t t=1,T

K_t=K_t-1+(1-a)D K_t "t t=1,T

L_t=L_t-1+D L_t "t t=1,T

(1-m)R_t=W_at+L_t+dK_t+p_cK_t "t t=1,T

W_at=g K_t+C_mL_t "t t=1,T

0<a<1,0<m<1,0<h<1,K_t>0, L_t>0, DK_t>0, DL_t>0 "t t=1,T

K_0, L₀,а, d,p_c,g, C_m- заданы

Здесь Т- конец рассматриваемого периода, а- доля выплат в общем потоке поступления средств, h - коэффициент штрафа, DK_t-величина поступления оборотного капитала в период t, DL_t- величина поступления фонда оплаты труда в период t.

Все остальные обозначения смотри в п.1.

Глава 2. Математический анализ моделей роста доходности страховой компании

§1 Математические анализ модели роста доходности страховой компании

Рассмотрим простейший аналог модели, приведенный в §2 главы 1. Приведем ее формулировку:

Максимизировать

?

ò (aI(t) + (1-a) R(t)) e^-rt dt

0

при условии

(1-m)R(t)=gK(t)+CmL(t)+L(t)+dK(t)+K’(t)+p(t)K, 0<d<1

p(t)³pc,0<g+d+p<1,0<a<1, 0<m<1

L(0)=L₀, L₀>0 K(0)= K₀, K₀>0

K₀ - начальный капитал фирмы, L₀ - начальное значение фонда оплаты труда. Осуществим некоторые упрощения.

Предположим, что p(t)=pc. (1.1)

Учитывая (2.1) (гл.1) и тот факт, что F(K(t),L(t)) однородна и построив функцию Лагранжа, получим:

W(t)=(1- a+am)Lj(K(t)/L(t))e^-rt + l(t)( -(1-m)L(t)j(K(t)/L(t)) + (g+d+pc)K(t) + (Cm + 1)L(t) + K’(t))

В результате исходная модель приводится к виду:

?

ò W(t) dt ®max (1.2)

0

при условиях

L(0)=L₀, K(0)=K₀ (1.3)

0<g+d+pc<1,0<a<1, 0<m<1,0<Cm<1 (1.4)

Далее, выпишем систему уравнений Эйлера - Лагранжа, вытекающую из (1.2)-(1.4)

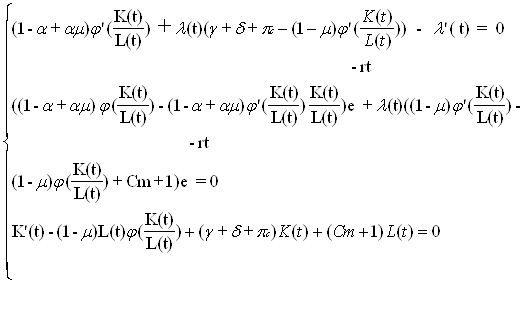
Перепишем последнюю систему в удобном виде.

l¢(t)=(1-a+am)j’()e^-rt+l(t)(g+d+pc-(1-m)j’()

e^-rt(1-a+am)(j()-j’())+l(t)((1-m)(j’()-j())+ Cm+1)=0

K’(t)-(1-m)L(t)j( )+(g+d+pc)K(t)+(Cm+1)L(t)=0 (1.5)

Обозначим k(t)=K(t)/L(t) и продифференцируем по t

k’(t)= (1.6)

Из (1.5) учитывая, что n(t)=(dL/dt)/L(t), получим:

K’(t)/L(t) = k’(t)+ k (t)n(t) (1.7)

ля упрощения выписанных выше выражений введем еще одно обозначение: z(k) = j’(k) k -j(k) (1.8)

Функция j(k) построена на основе F(,1) и поэтому для нее выполняются следующие свойства:

a)  j¢(k)>0

b)  j¢¢(k)<0

c)  j’(k) ® ? для k ® 0

d)  j’(k) ® 0 для k ® ?

Разделив последнее уравнение из (1.5) на L(t) и учтя обозначения, получим:

l’(t)= (1-a+am)j’(k(t))e^-rt+l(t)(g+d+pc-(1-m)j’(k(t))) (1.9)

l(t) =( 1-a+am)z(k(t))e^-rt /((1-m)z(k(t))+Cm+ 1) (1.10)

k’(t)=(1-m)j(k(t))-(g+d+pc)k(t)- (Cm+1) (1.11)

Продифференцировав (1.10) по t, получим:

-rt

l¢(t)=2 -rl(t) (1.12)

Учитывая, что

z’(k(t)) =j’’(k(t))k’(t)k(t) (1.13),

получаем, что формула (1.12) примет вид.

-rt

l¢(t)=2-rl(t) (1.14)

Подставляя в (1.14) соотношения (1.9) и (1.10), выясним, что темп изменения капиталовооруженности вычисляется по формуле:

k’(t) =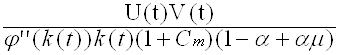 (1.15)

где

U(t) = (1 -m ) z(k(t)) + 1 + Cm

V(t) =(1-a+am)(j¢(k(t))U(t) + z(k(t))(r + d+g+pc-(1-m)j¢(k(t)))

Проведем качественный анализ уравнения ( 1.15 ).

Так как j¢(k) <0 для k >0, знаменатель в ( 1.15 ) отрицателен.(Мы предполагаем, что (1-a+am)(1+Cm)>0).

Далее из условий на функцию j(k) для z(k)=j¢(k)k-j(k) получаем z(k)£0 и z(k)® 0 при k ®0, и z(k) ® - ? при к ® ?. Для малых k

получаем U>0, V>0, так как j¢(k) - большое число, то k’<0. Для больших k получаем U<0, V<0, так как z(k) ® - ?, следовательно k’ <0. Из монотонного убывания U и V, что каждое из рассматриваемых уравнений U=0 и V=0 имеет единственный корень.

Таким образом область разбивается на три участка: kÎ[0,k₁),

k Î[ k₁, k₂),kÎ[ k₂,¥)

Из рисунка 1 видно, что существует одна точка не устойчивого равновесия k₁(m) и две точки 0 и k₂(m) устойчивого равновесия. Нетрудно видеть, что k₁(m) и k₂(a,m) монотонно возрастающие функции по m. Если начальное значение k₀=K₀/L₀ меньше чем k₁(m), тогда k® 0 и фирма гибнет. В противном случае размеры фирмы стабилизируются и стремятся к k₂(m). Следовательно мы можем рассматривать k₂(m) как оптимальный размер фирмы для данных значений параметров управления a,m,g,d,Wr,Cm. Таким образом, если заданы величины указанных выше параметров, то по величине k(t)= может быть оценено качество начального состояния и перспективы развития страховой компании.

Предлагается следующий путь:

Если <K(0), то необходимы меры по росту капитала или уменьшению L(t).Если есть возможность увеличить капитал, например за счет кредита, то получаем следующую задачу:

>K(0)

DK(t)®max

Если нет никакой возможности по увеличению капитала, то уменьшают фонд оплаты труда. В этом случае задача выглядит следующим образом:

>K(0)

L(t)*<L(t)<L(t)**

DL(t)®min

Приведем пример расчетов оптимального размера фирмы.

Рассмотрим влияние изменений параметра управления a на оптимальный размер страховой компании. Данные для расчета были предоставлены компанией Росгосстрах. Предполагается, что d=0.13, g=0.03, m= 0.1, C_m=0.8. Тогда зависимость k₁, k₂ представлены в таблице 1.

k/a	0	¼	1/2	¾	1
k1	7.2	7.2	7.2	7.2	7.2
k2	3.49	3.39	3.15	3.13	2.93

Таб.1

Можно исследовать значения k₁ и k₂ для других значений параметров, полагая m= 0.05, получаем таблицу 2.

a	0	1/4	1/2	3/4	1
k1	6.8	6.8	6.8	6.8	6.8
k2	3.4	3.23	3.15	3.13	3

Таб.2

Окончательно заметим, что изменение ставки комиссионного вознаграждения m при фиксированном капитале К ведет к уменьшению капиталовооруженности k.

§2 Математический анализ многомерной модели роста доходности страховых компаний

Рассматриваемая модель имеет вид:

Максимизировать

m R(t) + (1-a) R(t)) e^-rt dt

при условии

(1-m)R(t)=+(Cm+1)L(t) + dK(t)+ K’(t)+ p(t)K,

0<d<1, p(t)³pc, 0<g+d+p<1,0<a<1, 0<m<1

L(0)= L₀, L₀>0 K(0)= K₀,K₀>0

K₀ - начальный оборотный капитал фирмы, L₀ - начальный фонд оплаты труда штатных работников.

Будем рассматривать случай для n=2. Тогда рассматриваемая модель примет вид:

Максимизировать

(am (b1+b2)R(t) + (1-a) R(t)) e ^-rt dt

при условии

(1-m)R(t)=g(K1(t)+K2(t))+CmL(t)+L(t)+dK(t)+K’(t)+p(t)K(t),

0<d<1, p(t)³pc, 0<g+d+p<1, 0<a<1, 0<m<1

L(0)=L₀, L₀>0 K(0)= K₀, K₀>0

Выпишем функцию Лагранжа, учитывая (2.3) (гл.1) для случая n=2,(1.1) и тот факт, что F(K₁(t), K₂(t),L(t)) однородна, получим:

W(t)=(1- a+am(b1+b2))L(t)je^-rt+

l(t)(-(1-m)L(t) j + (g+d+pc)K(t) + (Cm + 1)L(t) + K’(t))

В результате исходная модель примет вид:

 W(t) dt ® max (2.1)

при условиях L(0)=L₀, K(0)=K₀ (2.2)

0<d<1, 0<g+d+p_c<1, 0<a<1, 0<m<1 (2.3)

Далее, выпишем систему уравнений Эйлера - Лагранжа, вытекающую из (2.1)-(2.3)

(1-a+am(b1+b2))j’k1/le^-rt+l(t)(g+d+pc-(1-m)

j’  )-l’(t)=0

(1-a+am(b1+b2))j’k2/l)e^-rt+l(t)(g+d+pc-(1-m)j’k2/l) -l’(t)=0

l(t)=[(1-a+am(b1+b2))(j’k1/l+ j’k2/l -j+e^-rt]/[(1-m)(j’k1/l+

j’ -j-Cm-1]

K’(t)-(1-m)L(t)j  +(g+d+pc)K(t)+(Cm+1)L(t)=0

Перепишем последнюю систему в удобном виде.

l’(t)=(1-a+am(b1+b2))j’k1/l l)e^-rt+

l(t)(g+d+pc-(1-m)j’k1/l l)

l’(t)=(1-a+am(b1+b2))j’k2/l le^-rt+

l(t)(g+d+pc-(1-m)j’k2/l l)

l(t)=[(1-a+am(b1+b2))(j’k1/l+ j’k2/l -j+e^-rt]/[(1-m)(j’k1/l+

j’ -j-Cm-1]

K’(t)=(1-m)L(t)j -(g+d+pc)K(t)-(Cm+1)L(t) (2.4)

Обозначим

k(t)=K(t)/L(t), k1(t)=K1(t)/L(t), k2(t)=K2(t)/L(t) и n(t)=(dL/dt)/L (2.5)

и проведем аналогичные §1 рассуждения. Тогда справедливо соотношение (1.7).

Для упрощения полученной системы введем еще одно обозначение:

z(k(t)) = j’_k1(t)(k1(t),k2(t)) k1(t) +j’_k2(t)(k1(t),k2(t)) k2(t)-j(k1(t),k2(t))

Разделив уравнение (2.4) на L(t) и учитывая обозначения, получим:

l’(t)=(1-a+am(b1+b2))j’k1(k1(t), k2(t))e^-rt+

l(t)(g+d+pc-(1-m)j’k1(k1(t), k2(t))) (2.6)

l’(t)=(1-a+am(b1+b2))j’k2(k1(t),k2(t))e^-rt+

l(t)(g+d+pc-(1-m)j’k2(k1(t), k2(t))) (2.7)

l(t)=[(1-a+am(b1+b2))z(k1(t),k2(t))e^-rt]/[(1-m)(z(k1(t),k2(t))+Cm+1] (2.8)

k’(t)=(1-m)j(k1(t),k2(t))-(g+d+pc)k(t)-(Cm+1) (2.9)

Продифференцируем (2.8) по t. Получим:

-rt

l¢(t)=2 -rl(t) (2.10)

Учитывая, что z’(k1(t),k2(t)) =j’’k1k1( k1(t),k2(t))k’1(t)k1(t) +j’’k2k2( k1(t),k2(t))k’2(t)k2(t), получаем, что формула (2.10) примет вид

l¢(t) =e ^-rt(j’’k1k1( k1(t),k2(t))k’1(t)k1(t) +j’’k2k2( k1(t),k2(t))k’2(t)k2(t))(1- a+am(b1+b2))(Cm+1) / [(1 -m)z(k1(t),k2(t)) + Cm +1] ² - rl(t) (2.11)

Подставляем в (2.11) соотношения (2.6) и (2.8), (2.7) и (2.8) соответственно, получим, что темп изменения капиталовооруженности вычисляется по формулам:

k’(t)=(1-m)j(k1(t),k2(t))-(g+d+pc)k(t)-(Cm+1)

k’1(t)=

k’2(t)=

где

U(t)= (1 -m)z(k1(t),k2(t)) + Cm +1

V1(t)= Cm +1+z(k1(t),k2(t))((1 -m) +j’k1( k1(t),k2(t))(1 -m)-(g+d+pc+r))

V2(t)= Cm +1+z(k1(t),k2(t))((1 -m) +j’k2( k1(t),k2(t))(1 -m)-(g+d+pc+r))

Рассмотрим случай, когда оба агента участвуют в формировании капитала фирмы в равных долях. Тогда (при n=1) рассматриваемая модель сводится к сличаю приведенному в §1. Однако, если доли не равны, то приходим к качественно новой задаче.

§3 Математический анализ многосекторной модели роста доходности страховой компании

Напишем ее формулировку.

Максимизировать

¥ n n -rt

J(t)=ò( åaIj(t)+ å(1-a)Rj(t))e dt