АНАЛИЗ СЕТЕВОГО ГРАФИКА

2. АНАЛИЗ СЕТЕВОГО ГРАФИКА

 

Одно из важнейших понятий СПУ – понятие пути (маршрута). Путь (маршрут) – любая последовательность работ, в которой конечное событие каждой работы совпадает с начальным событием следующей за ней работы. Наибольший интерес представляет полный путь – любой путь, начало которого совпадает с начальным событием сети, а конец – с завершающим. Наиболее продолжительный полный путь называют критическим. Критическими называют также работы и события, расположенные на этом пути.

Проведем анализ сетевого графика:

Полные пути	Продолжительность (сутки)
	Нормальный режим	Ускоренный режим
1 – 2 – 5 – 6	19	13
1 – 3 –6	22	11
1 – 2 - 4- 5- 6	29	17

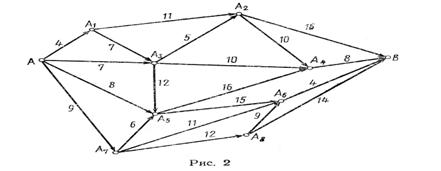
Полными путями при нормальном режиме будут:

путь 1-2-5-6 (продолжительностью 4 + 6 +9=19 суток)

путь 1-3-6 (продолжительностью 10 +12 = 22 суток)

путь 1-2-4-5-6 (продолжительностью 4 + 5+11 +9=29 суток)

Полными путями при ускоренном режиме будут:

путь 1-2-5-6 (продолжительностью 3 + 4 +6=13 суток)

путь 1-3-6 (продолжительностью 5 + 6=11 суток)

путь 1-2-4-5-6 (продолжительностью 3 + 2+6 +6=17 суток)

Критическим путем будет путь 1-2-4-5-6, продолжительность которого при нормальном режиме составит 29 суток, а при ускоренном режиме – 17 суток.

Максимальный срок завершения всей совокупности работ составит 29 суток, а минимальный – 17 суток. Требуется довести продолжительность работ при нормальном режиме с 29 до 19 суток, а при ускоренном режиме с 17 суток до 19 суток.

3. ОПТИМИЗАЦИЯ СЕТЕВОГО ГРАФИКА

С каждой работой, имеющей определенный неизменный объем, связаны затраты на ее выполнение. Как правило, затраты на выполнение работы возрастают с уменьшением ее продолжительности и снижаются при увеличении ее продолжительности.

В связи с этим возможны варианты организации работ, отличающиеся продолжительностью его выполнения и затратами на его выполнение.

Оптимизация сетевого графика представляет собой процесс улучшения организации выполнения комплекса работ с учетом срока его выполнения. Она проводится с целью сокращения длины критического пути, рационализации использования ресурсов.

Оптимизация сетевого графика может осуществляться по следующим двум критериям:

1.  минимизация времени выполнения комплекса работ при заданных затратах на это выполнение;

2.  минимизация затрат на выполнение комплекса работ при заданном времени этого выполнения.

Целью оптимизации по критерию является сокращение времени выполнения проекта в целом. Эта оптимизация имеет смысл только в том случае, когда длительность выполнения работ может быть уменьшена за счет дополнительных ресурсов, что влечет к повышению затрат на выполнение работ. Для оценки величины дополнительных затрат, связанных с ускорением выполнения той или иной работы, используются либо нормативы, либо данные о выполнении аналогичных работ в прошлом.

Таким образом, нельзя добиться выполнения комплекса работ одновременно в минимальные сроки и с наименьшими затратами.

Оптимизацию можно провести двумя способами:

1.  способ заключается в уменьшении продолжительности выполнения работ, осуществляемых в нормальном режиме, начиная с тех, которые дают наименьший прирост затрат;

2.  способ заключается в увеличении продолжительности выполнения работ, осуществляемых в ускоренном режиме, начиная с тех, которые дают наибольший прирост затрат.

Обязательное условие – оптимальные затраты, определяемые любым из указанных способов, должны иметь одинаковую величину.

Требуется оптимизировать по критерию минимизации затрат сетевой график при заданно продолжительности всего комплекса работ за 19 суток.

Представим решение поставленной задачи первым способом в таблице:

№ шага	Суточный прирост затрат	Работа	Количество сокращаемых суток	Продолжительность полного пути			Общий прирост затрат
				1-2-5-6	1-3-6	1-2-4-5-6
0	-	-	-	19	22	29	-
1	10	2-4	3 ( 3)	-	-	26	30
2	15	1-3	5 ( 3)	-	19	-	45
3	20	1-2	1 (1)	18	-	25	20
4	25	2-5	2 -	-	-	-	-
5	30	3-6	6 -	-	-	-	-
6	35	4-5	5 (5)	-	-	20	175
7	40	5-6	1 (3)	17	-	19	40
В С Е Г О							310

В этой таблице работы расположены в порядке возрастания суточного прироста затрат на снижение их продолжительности. Наименования полных путей и их продолжительность взяты из результатов предыдущего анализа сетевого графика для рассматриваемого нормального варианта. Максимально возможное количество сокращаемых суток для каждой работы указано в скобках.

На первом шаге рассматривается работа 2-4, которая входит в третий полный путь и ее продолжительность может быть сокращена на все 3 суток, т.к. продолжительность третьего полного пути, а следовательно и всего комплекса работ, все равно будет выше требуемой. Такое снижение продолжительности рассматриваемой работы на 3 суток приведет к увеличению затрат на выполнение этой работы, а следовательно и всего комплекса работ в размере: 3*10=30 у.е.

На втором шаге рассматриваемая работа 1-3 , которая входит во второй полный путь и ее продолжительность может быть сокращена на 3 суток , (из 5 возможных), т.к. при этом продолжительность второго пути, в который она входит становится равной заданной : 22-3=19.Аналогично рассчитываем затраты на такое сокращение : 3*15=45

На третьем шаге рассматриваемая работа 1-2 входит в первый и третий полный путь . Она может быть сокращена на максимально возможную величину (указанную в скобках) на 1, т.к при этом продолжительность третьего полного пути все равно будет выше требуемого . Аналогично рассчитываем затраты на такое сокращение : 1*20=20

На четвертом шаге рассматриваемая работа 2-5 входит в первый полный путь и ее продолжительность сокращать не нужно , т.к.продолжительность первого полного пути меньше требуемого .

На пятом шаге рассматриваемая работа 3-6 входит во второй полный путь и ее продолжительность сокращать не нужно , т.к.продолжительность второго полного пути меньше требуемого .

На шестом шаге рассматриваемая работа 4-5 входит в третий полный путь. Она может быть сокращена на максимально возможную величину (указанную в скобках) на 5, т.к при этом продолжительность третьего полного пути все равно будет выше требуемого . Аналогично рассчитываем затраты на такое сокращение : 5*35=175

На седьмом шаге рассматриваемая работа 5-6 , которая входит в первый и третий полный путь и ее продолжительность может быть сокращена на 1 сутки , (из 3 возможных), т.к. при этом продолжительность третьего полного пути, в который она входит становится равной заданной : 20-1=19, а продолжительность первого полного пути меньше требуемого. Аналогично рассчитываем затраты на такое сокращение : 1*40=40

Подсчитав суммарные дополнительные затраты на произведенное сокращение продолжительностей работ (310 у.е.) и зная первоначальную стоимость (1060 у.е.) всего комплекса работ в рассматриваемом нормальном варианте его выполнения, получим, что при снижении продолжительности выполнения всего комплекса работ с 29 суток до 19 суток оптимальные затраты составят 1060+310=1370 (у.е.).

Представим решение поставленной задачи вторым способом в таблице:

№ шага	Суточный прирост затрат	Работа	Количество наращиваемых суток	Продолжительность полного пути			Общее снижение затрат
				1-2-5-6	1-3-6	1-2-4-5-6
0	-	-	-	13	11	17	-
1	40	5-6	3 (2)	15		19	-80
2	35	4-5	5 (2)	-	-	-	-
3	30	3-6	6 (6)	-	17	-	-180
4	25	2-5	2 (2)	17	-	-	-50
5	20	1-2	1 (1)	-	-	-	-
6	15	1-3	5 (2)	-	19	-	-30
7	10	2-4	3 -	-	-	-	-
В С Е Г О							-340

Отличие этой таблицы от предыдущей состоит в том, что в ней работы располагаются в порядке убывания их суточного прироста затрат на изменение (увеличение) их продолжительности. Продолжительность полных путей здесь соответствует другому варианту и взята из результатов предыдущего анализа сетевого графика для рассматриваемого ускоренного варианта выполнения всего комплекса работ. В последней колонке теперь будет рассчитываться уже снижение затрат.

На первом шаге продолжительность работы 5-6 может быть увеличена только на 2 суток из возможных (3), т.к. при этом продолжительность третьего полного пути станет как требуемая в задании. Тогда затраты на эту работу, с более поздним сроком выполнения, снизятся на 2·40=80 (у.е.), т.е. -80 у.е.

Второй шаг 4-5придется не использовать, т.к. увеличение продолжительности соответствующей ему работы 43-5 приведет к недопустимому увеличению продолжительности третьего полного пути, а следовательно, и всего комплекса работ.

Рассматривая работу 3-6 на третьем шаге, увеличиваем продолжительность второго пути на 6 суток, т.к. продолжительность второго полного пути станет как требуемая в задании.

На четвертом шаге продолжительность работы 2-5 в первом полном пути можно увеличить на максимально возможное число суток.

Пятый шаг 1-2 мы не используем.

Шестой шаг 1-3 увеличиваем на 2 из 5 возможных , т.к. при этом продолжительность второго полного пути станет как требуемая в задании -19

Седьмой шаг 2-4 мы не используем.

Подсчитав суммарное снижение затрат из-за произведенного увеличения продолжительностей работ (-340 у.е.) и зная первоначальную стоимость (1710 у.е.) всего комплекса работ в рассматриваемом ускоренном варианте его выполнения, получим, что при увеличении продолжительности выполнения всего комплекса работ с 17 суток до 19 суток оптимальные затраты составят 1710-340=1370 (у.е.).

Итоговые результаты, полученные обоими способами оптимизации, должны совпадать. Проверим это:

1)  продолжительности соответствующих полных путей после оптимизации совпадают – 19,19,17;

2)  стоимости выполнения всего комплекса работ после оптимизации совпадают – 1370.

ЗАКЛЮЧЕНИЕ

В данной курсовой работе был построен сетевой график, проведен его анализ, и произведена оптимизация сетевого графика. При использовании данных методик можно найти критический путь сетевого графика. В результате оптимизации определили минимальную стоимость комплекса работ при заданной продолжительности его выполнения.

Значимость проделанной работы заключается в том, что применение предложенных методик, во-первых – позволяет точно судить об оптимальности сетевых графиков любой сложности, а во-вторых – сокращает затраты на сетевое планирование в целом, прежде всего, за счёт сокращения длительности разработки оптимальных сетевых графиков.

Анализ сетевого графика заключается в том, чтобы выявить резервы времени работ, не лежащих на критическом пути, и направить их на работы, лимитирующие срок завершения комплекса работ. Результатом этого является сокращение продолжительности критического пути.

Список литературы

1.  Абланская Л.В., Бабешко Л.О., Баусов Л.И. Экономико-математическое моделирование: М.: Экзамен, 2006г. – 800с.

2.  1. Баканов М.И., Шеремет А.Д. Теория экономического анализа: Учебник. - М.: Финансы и статистика, 1997.

3.  Дрогобыцкого И.Н Экономико-математическое моделирование: М.: Экзамен, 2004г. – 323с.

4.  Казаков О.Л., Миненко С.Н., Смирнов Г.Б. Экономико-математическое моделирование: учебно-методическое пособие. – М.: МГИУ, 2006. - 136 с.

5.  Конюховский П.В Математические методы исследования операций в экономике: С-Петербург: Питер 2003г. - 208 с.